[Paper Review] Analytic-Splatting

[논문 리뷰] Analytic-Splatting : Anti-Aliased 3D Gaussian Splatting via Analytic Integration

Analytic-Splatting : Anti-Aliased 3D Gaussian Splatting via Analytic Integration

Zhihao Liang

ECCV 2024.

[Arxiv] [Project Page] [Github]

Introduction

3D Gaussian Splatting(3DGS)은 최근 GPU 친화적인 rasterization을 제안하며 노벨 뷰 합성을 위한 고품질 및 실시간 렌더링을 달성했다. NeRF의 ray marching은 이미지 평면에서 픽셀과 교차하는 광선을 따라 sample의 opacity를 누적하여 픽셀을 렌더링한다. 반면, 3DGS는 장면을 3D Gaussian의 집합으로 표현하고, 렌더링 시 3D Gaussian을 2D Gaussian으로 이미지 평면에 투영하고, 픽셀과 겹치는 Gaussian과 연관된 값을 조회한 후, 이 조회된 값과 속성을 누적하여 픽셀을 음영 처리한다.

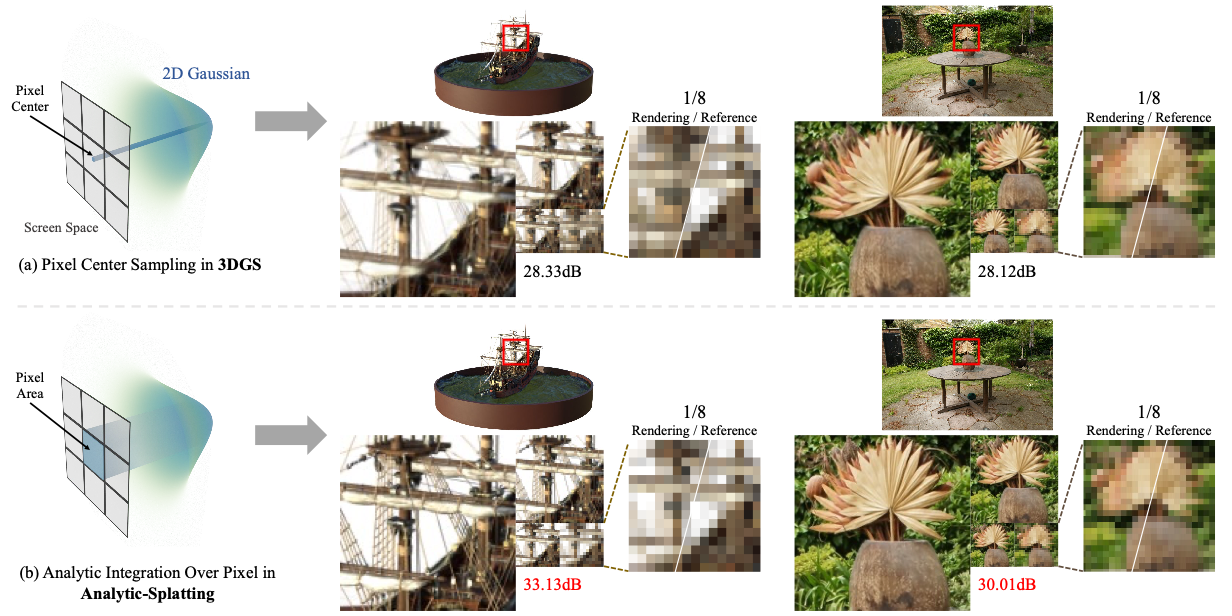
하지만, multi-view 이미지가 다양한 거리에서 캡처되거나 렌더링할 novel view가 캡처된 이미지의 해상도와 다를 때 성능이 크게 저하된다는 단점이 있다. 주된 이유는 픽셀의 footprint가 다른 해상도에서 변하기 때문이며, 3DGS는 해당 Gaussian 값을 검색할 때 각 픽셀을 isolated point(즉 픽셀 중심)으로 처리하기 때문에 이러한 변화에 둔감하다. 아래 그림의 a는 이를 보여준다.

footprint는 화면 공간의 픽셀 창 영역과 World space의 가우스 신호 커버 영역 사이의 비율로 정의된다.

결과적으로, 3DGS는 특히 픽셀 footprint가 급격하게 변경될 때(예: zoom in/out으로 view를 합성할 때) Aliasing를 일으킬 수 있다.

세부사항을 살펴보면, 3DGS는 이미지 space에서 연속적인 신호를 일련의 $\alpha$-blending된 2D Gaussian으로 표현하며, 픽셀 음영 처리는 각 픽셀 영역 내에서 signal을 적분하는 과정이다.

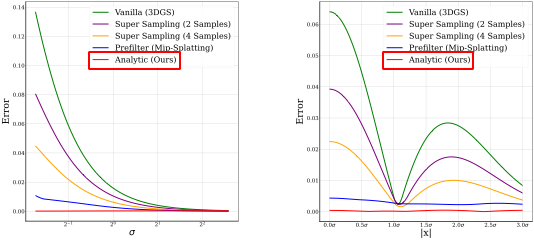
Aliasing은 제한된 sampling rate로 인해 발생하며, 특히 픽셀 footprint가 급격하게 변경될 때 나타난다. 이는 Sampling rate를 증가시키거나(예: Super samping을 사용) prefiltering 기술을 사용하여 이 문제를 완화할 수 있다. 예를 들어, Mip-Splatting은 prefiltering과 hybrid 필터링을 제시하여 대부분의 Anti-Aliasing 문제를 해결하지만, detail을 캡처하는 데는 제한적이다.

따라서 픽셀 창 영역 내에서 Gaussian 신호의 적분을 해결하는 것은 Anti-Aliasing과 세부 사항 캡처에 모두 중요하다.

이 논문에서는 3DGS에서 픽셀 음영을 재조사하고 Gaussian 신호의 Window 적분 반응에 대한 분석적 근사를 도입하여 Anti-Aliasing을 수행한다.

Analytic-Splatting은 2D Gaussian 저역 통과 필터로 픽셀 창을 근사하는 Mip-Splatting과 달리, 각 픽셀 영역 내에서 적분을 분석적으로 근사하여 Gaussian 신호의 고주파 성분을 억제하지 않으며 고품질의 세부 사항을 더 잘 보존할 수 있다.

Method

Revisit One-dimensional Gaussian Signal Response

이 섹션에서는 더 나은 이해를 위해 Window 영역 내의 1차원 Gaussian 신호의 적분을 예시로 든다.

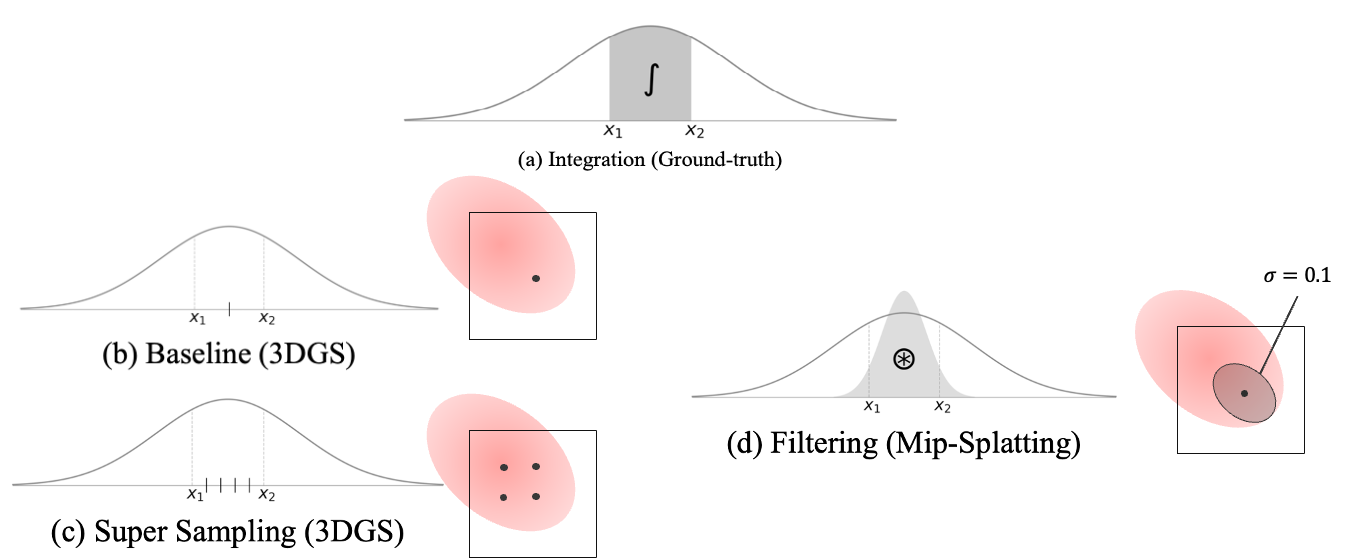
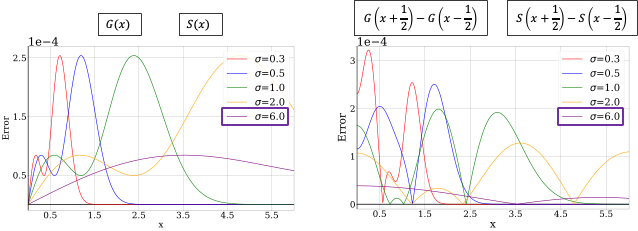
신호 $g(x)$와 창 영역 $[x_1, x_2]$가 주어지면, 이 영역 내에서 신호를 적분하여 반응 $\mathcal{I}g = \int{x_1}^{x_2} g(x) dx$ 을 얻고자 한다.(a)

• (b), (c) : 창 영역 내에서 몬테 카를로 샘플링을 사용하여 적분을 근사

  $\mathcal{I}g \approx \frac{x_2 - x_1}{N} \sum{i=1}^N g(x_i), x_i \in [x_1, x_2]$

  • (b) : 픽셀 중심에서 sampling (몬테 카를로 샘플링)

  • (c) : 샘플 수 $N$이 증가함에 따라 더 정확해지지만, 이 Super Sampling은 계산 부담 증가

Gaussian 신호가 연속적인 실수 값 함수라는 점을 고려할 때, Gaussian 적분을 분석적으로 근사하는 것이 더 정확하다.

• (d) : Mip-Splatting에서는 창 영역을 Gaussian 커널 $g_w$로 처리하고, Gaussian 신호와 Gaussian 커널의 합성 후 샘플링 결과로 적분을 근사g한다.($\mathcal{I}_g \approx g \circledast g_w$).
  • 이는 Gaussian 신호 $g$가 주로 고주파 성분(즉, 표준 편차 $\sigma$가 작을 때)으로 구성되어 있을 경우 큰 차이 발생

이러한 단점을 극복하기 위해, 창 영역 내에서 적분을 분석적으로 계산하고자 한다.

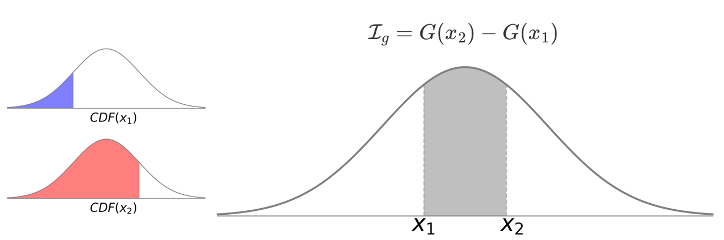
$[x_1, x_2]$ 내에서 정적분은 두 부정적분의 차이로 단순화할 수 있다. $G(x)$를 표준 Gaussian 분포 $g(x)$의 누적 분포 함수(CDF)로 정의하고, $g(x)$내에서 $[x_1, x_2]$의 정적분은 다음과 같이 표현될 수 있다:

\[\mathcal{I}_g = G(x_2) - G(x_1)\]

그러나 이 Gaussian 함수의 CDF(오차 함수 $\text{erf}$로 정의됨)는 닫힌 형태가 아니기 때문에 우리는 CDF $G(x)$를 근사한다.

$S(x)$는 표준 편차 $\sigma = 1$을 가진 CDF $G(x)$의 분석적 근사로 정의되며, 다음과 같이 정의된다:

\(S(x) = \frac{1}{1 + \exp(-1.6 \cdot x - 0.07 \cdot x^3)},\) 이 분석적 근사는 CDF G(x)의 유사한 특성을 포함한다. $S(x)$는 $\textit{비감소}$하며 $\textit{우측 연속}$이며, 다음을 만족한다:

\[\lim_{x \to -\infty} G(x) = \lim_{x \to -\infty} S(x) = 0 \quad \text{and} \quad \lim_{x \to \infty} G(x) = \lim_{x \to \infty} S(x) = 1.\]

$S(x)$의 곡선은 점 $(0,\frac{1}{2})$주위에서 $\textit{2-fold rotational symmetry}$을 가진다:

\[G(x) + G(-x) = S(x) + S(-x) = 1, \ \forall x \in \mathbb{R}.\]

다른 표준 편차를 가진 Gaussian 신호의 경우, $S(x)$의 $x$를 $\frac{1}{\sigma}$로 스케일링함으로써 CDF를 근사할 수 있다. $x$를 $S(x)$에서 $\sigma$의 역수로 스케일링한 것을 $S_\sigma(x)$로 표현한다.

요약하면, 샘플 $u$를 주어지고 창 영역을 1로 설정하면, 영역 $[u - \frac{1}{2}, u + \frac{1}{2}]$ 내에서 Gaussian 신호 $g(x)$의 적분 $\mathcal{I}_g(u)$는 다음과 같이 정의된다:

\[\mathcal{I}_g(u) = \int{u - \frac{1}{2}}^{u + \frac{1}{2}} g(x) dx = G(u + \frac{1}{2}) - G(u - \frac{1}{2}).\]

또한, 정의에 따라 $S(x)$을 적용하여 $\mathcal{I}_g(u)$의 적분을 근사하면 다음과 같다:

\[\mathcal{I}_g(u) \approx S(u + \frac{1}{2}) - S(u - \frac{1}{2}).\]

Analytic-Splatting

앞의 1차원 Gaussian 신호 적분을 통해, 각 픽셀 창 영역 내의 투영된 2D Gaussian의 적분을 근사하려고 한다.

수학적으로, $C(u) = \sum_{i\in N} T_i g^\text{2D}_i(u | \hat{\mu_i}, \hat{\Sigma_i})\alpha_i c_i$에서 $g^\text{2D}(u)$를 근사된 적분 $\mathcal{I}_g^\text{2D}(u)$로 대체할 수 있다.

2D 스크린 공간에서 픽셀 $u = [u_x, u_y]^\top$는 창 영역 $\Omega_{u}$에 해당한다. 이 창 영역 내의 Gaussian 신호 적분은 다음과 같이 표현된다:

\[\mathcal{I}_g^\text{2D}(u) = \int_{u_x - \frac{1}{2}}^{u_x + \frac{1}{2}}\int_{u_y - \frac{1}{2}}^{u_y + \frac{1}{2}} \exp\left(-\frac{a}{2} (x - \hat{\mu}_x)^2 -\frac{c}{2} (y - \hat{\mu}_y)^2 -b (x - \hat{\mu}_x) (y - \hat{\mu}_y) \right) dx dy\]

이 적분에서 correction term $b (x - \hat{\mu}_x) (y - \hat{\mu}_y)$을 다루는 것은 불가능하다.

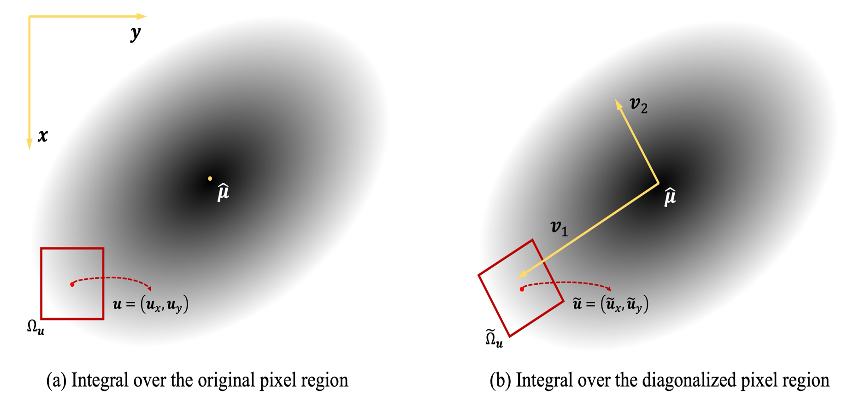
correction term을 해석하고 적분을 가능하게 하기 위해, 2D Gaussian $g^\text{2D}$의 공분산 행렬 $\hat{\Sigma}$를 대각화하고 그림 b에 나타난 것처럼 적분 영역을 회전시켜 두 독립적인 1D Gaussian 적분의 곱으로 적분을 근사한다.

구체적으로, 공분산 행렬 $\hat{\Sigma}$에 대해 고유값 분해를 수행하여 고유값 ${\lambda_1, \lambda_2}$와 해당 고유벡터 ${v_1, v_2}$를 얻는다. 대각화 후에는 $g^\text{2D}$의 평균 벡터인 $\hat{\mu} = [\hat{\mu}_x, \hat{\mu}_y]^\top$을 원점으로 하고 고유벡터 $[{v}_1, {v}_2]$을 축으로 하는 새로운 좌표계를 구성한다.

이 좌표계에서, 주어진 픽셀 ${u} = [u_x, u_v]^\top$에 대해, $g^\text{2D}$를 두 독립적인 1D Gaussian의 곱으로 다시 작성한다:

\[g^\text{2D}({u}) = \exp\left(-\frac{1}{2\lambda_1}\tilde{u}_x^2\right) \exp\left(-\frac{1}{2\lambda_2}\tilde{u}_y^2\right)\]

여기서 $\tilde{u} = \left [ \tilde{u}_x, \tilde{u}_y \right ]^\top $은 픽셀 중심의 대각화된 좌표를 나타낸다.

대각화 후, 픽셀 적분 영역 $\Omega_{u}$을 픽셀 중심을 따라 회전시켜 고유벡터와 정렬하고, 적분을 근사하기 위해 $ \tilde{\Omega}_{u} $를 얻는다.

따라서 $ \mathcal{I}g^\text{2D}(u) $의 적분은 다음과 같이 근사된다:

\[\mathcal{I}g^\text{2D}(u) \approx \int{\tilde{\Omega}_u}g^\text{2D}(u) d{u}= 2\pi\sigma_1\sigma_2 \left[S{\sigma_1}(\tilde{u}_x + \frac{1}{2}) - S{\sigma_1}(\tilde{u}_x - \frac{1}{2})\right ]\left[S{\sigma_2}(\tilde{u}_y + \frac{1}{2}) - S{\sigma_2}(\tilde{u}_y - \frac{1}{2})\right ].\]

여기서 $\sigma_{\ast}$는 각기 다른 표준 편차를 가진 Gaussian 신호에 해당한다.

$\sigma_1 = \sqrt{\lambda_1}$과 $\sigma_2 = \sqrt{\lambda_2}$는 각각 두 고유벡터를 따라 독립적인 Gaussian 신호의 표준 편차를 나타낸다. 요약하면, Analytic-Splatting에서 $C(u)$는 다음과 같이 제공된다:

\[{C}({u}) = \sum_{i \in N} T_i \mathcal{I}_{g_i}^\text{2D}({u} | \hat{\mu_i}, \hat{\Sigma}_i)\alpha_i c_i, \quad T_i = \prod_{j=1}^{i-1}(1 - \mathcal{I}_{g_j}^\text{2D}({u} | \hat{\mu_j}, \hat{\Sigma_j}) \alpha_j),\] \[\mathcal{I}{g}^\text{2D}({u}) = 2\pi\sigma_1\sigma_2 \left[ S{\sigma_1}(\tilde{u}_x + \frac{1}{2}) - S{\sigma_1}(\tilde{u}x - \frac{1}{2}) \right ]\left[S{\sigma_2}(\tilde{u}_y + \frac{1}{2}) - S{\sigma_2}(\tilde{u}_y - \frac{1}{2}) \right].\]

Experiments

왼쪽은 CDF와 근사된 시그모이드의 차를, 오른쪽은 샘플 영역 1이 주어졌을 때, 실제와 근사값의 차이를 가우시안 함수의 표준편차별로 나타낸 그래프이다.

표준편차가 클 수록 가우시안의 크기가 커져 픽셀 영역을 채우는 일이 많아지고, 근사값이 유사해진다.

각각 표준편차와 변수 분포에 따른 근사 오차를 다른 방법들과 비교한 그래프로, 근사 오차는 이 paper가 가장 적은 것을 확인할 수 있다.

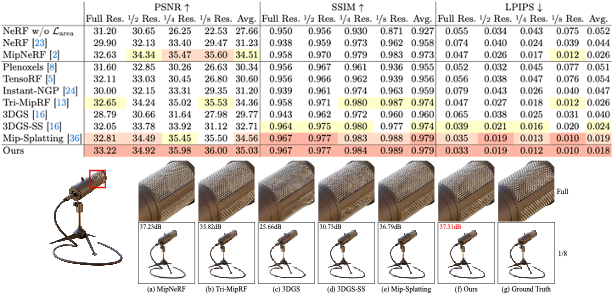
Blender Synthetic dataset 에서 다양한 method를 평가한 결과이다.

Analytic Splatting이 미세하게 가장 좋은 결과를 보이는 것을 알 수 있지만, 필자가 눈으로 보기에는 드라마틱한 시각적인 향상은 없다ㅓ.

실제 수치적으로도 Mip Splatting과 큰 차이가 없기도 하고 더 많은 연산을 요구하기 때문에 계산 비용이 증가하고, 속도를 느리게 한다.

하지만 3D 가우시안 Splatting에서 Gaussian 신호를 해석하고 적분을 로지스틱 함수로 근사해서 분석적이고 정확한 근사를 제안하였다는 점에서 의의가 있는 논문이라고 생각한다.