[Paper Review] CoIBA
[논문 리뷰] Comprehensive Information Bottleneck for Unveiling Universal Attribution to Interpret Vision Transformers
Comprehensive Information Bottleneck for Unveiling Universal Attribution to Interpret Vision Transformers
Jung-Ho Hong, Ho-Joong Kim, Kyu-Sung Jeon, Seong-Whan Lee
CVPR 2025
[Arxiv]
Background
ViT와 모델 해석의 필요성
ViT(Vision Transformer, ViT)는 입력 이미지를 patch(작은 영역)로 분할한 뒤 각 patch를 embedding하여 일련의 token으로 처리하는 신경망 모델이다.
ViT는 여러 layer의 self-attention 메커니즘을 통해 장기 의존성을 효과적으로 학습하며, ImageNet 등 다양한 시각 task에서 뛰어난 성능을 보인다.
그러나 수백만 개의 매개변수를 가진 복잡한 구조 탓에 블랙박스처럼 동작하여 내부 결정 과정을 이해하기 어렵다.
이러한 불투명성은 모델의 신뢰성을 낮추고, 예측 실패의 원인을 분석하거나 안전성이 중요한 분야(의료 영상, 자율주행 등)에서 ViT를 활용하는 데 걸림돌이 된다.
이에 따라 모델 해석과 설명 가능 인공지능(XAI)에 대한 요구가 커지고 있다.
특히, 입력 이미지의 어떤 부분이 모델 예측에 영향을 주었는지를 나타내는 특징 중요도 시각화(특성 기여도 map)가 널리 활용된다.
정보 병목 이론 (Information Bottleneck)
정보 병목 이론은 입력 변수 $X$에서 불필요한 정보를 버리고 목표 변수 $Y$와 관련된 정보만 함축하는 latent representation $Z$를 찾는 원리이다.
구체적으로, $Z$는 $X$로부터 추출된 Bottleneck representation이며, $Z$가 의미있는 정보만 남기도록 $X$와 $Z$ 사이의 상호정보(mutual information) $I(X;Z)$를 줄이는 한편, $Z$가 예측 대상 $Y$에 대한 정보를 충분히 담도록 $I(Z;Y)$를 늘리는 task를 푼다.
이 두 목표는 동시에 달성하기 어려우므로 다음과 같은 최적화 문제로 정식화된다.
\[\max_Z I(Z; Y)-\beta I(X; Z)\]여기서 $\beta$는 $Z$의 압축 정도(불필요한 정보 제거)를 조절하는 트레이드오프 계수이다.
상호정보 $I(U;V)$는 두 변수 $U, V$ 간의 공통된 정보의 양으로 정의되며, 확률분포 관점에서
\[I(U;V) = H(U) + H(V) - H(U, V) = H(U) - H(U\mid V)\]와 같이 표현된다 (여기서 $H(\cdot)$는 entropy, $H(U\mid V)$는 조건부 entropy).
상호정보는 KL divergence로도 나타낼 수 있는데, 분포 $P$와 $Q$ 사이의 KL divergence $D_{\mathrm{KL}}(P|Q)$는 두 분포 간 차이를 재는 척도이다.
예를 들어, 조건부 분포 $P(Z|X)$와 주변 분포 $P(Z)$를 이용하면
\[I(X;Z) = E_{X}\big[ D_{\mathrm{KL}}\left(P(Z\mid X)\|P(Z)\right) \big]\]으로 나타낼 수 있다.
정보 병목의 목표는 $Z$가 $Y$와 최대한 많은 정보를 공유하도록 ($I(Z;Y)$ 극대화) 하면서 $X$와 불필요한 정보는 공유하지 않도록 ($I(X;Z)$ 최소화) 학습시키는 것이다.
이 원리는 심층 신경망의 representation learning을 이끄는 이론적 기반으로도 사용되며, 모델의 내부 representation이 어떻게 목표 예측에 기여하는지 분석하는 데 응용되고 있다 .
IBA : 정보 병목을 이용한 특징 중요도 추정
정보 병목 기법을 활용한 특성 중요도 산출(IBA, Information Bottleneck Attribution)는 위 원리를 딥러닝 모델 설명에 적용한 방법이다.
IBA에서는 모델의 중간layer(예: ViT의 특정 layer 출력)을 $R_l$이라고 할 때, 해당 layer에 Bottleneck 변수 $Z_l$을 삽입하여 출력 활성값의 정보량을 조절한다.
IBA의 과정은 다음과 같다: 우선 $R_l$에 독립적인 noise $\epsilon_l$을 섞어 $Z_l$을 생성한다.
수식으로 $l$-번째 layer의 Bottleneck 출력은
\[Z_l = \lambda_l,R_l + (1 - \lambda_l)\epsilon_l\]로 정의된다. 여기서 $\lambda_l$은 $0\sim 1$ 사이의 댐핑 비율(damping ratio)로, learnable한 파라미터이다.
$\lambda_l=1$이면 $Z_l$에 noise이 섞이지 않고 원래 활성값 $R_l$를 그대로 통과시키며, $\lambda_l=0$이면 $R_l$를 완전히 차단하고 순수 noise $\epsilon_l$만 전달한다.
$\epsilon_l$은 $R_l$의 평균 $\mu_{R_l}$와 분산 $\sigma^2_{R_l}$을 갖는 가우시안 노이즈로 sampling하여, Bottleneck을 삽입해도 해당 layer의 통계적 분포를 유지하도록 설계된다.
이렇게 생성된 $Z_l$는 $R_l$에 포함된 정보를 부분적으로 압축한 representation으로 볼 수 있다.
IBA는 $\lambda_l$을 조정하여 $Z_l$가 예측에 필요한 정보만 남기도록 학습시킨다.
이를 위해 목표 함수로 상호정보의 차이를 최대화한다:
\[\max_{\lambda_l};; I(Z_l; Y);-; \beta,I(R_l; Z_l)\]- 첫 번째 항 $I(Z_l;Y)$는 Bottleneck 출력 $Z_l$과 레이블 $Y$ 간의 관련 정보를 의미
- 이는 $Z_l$가 예측에 얼마나 도움이 되는지를 나타낸다.
- 두 번째 항 $I(R_l;Z_l)$는 $Z_l$이 원래 활성값 $R_l$과 공유하는 정보로, $Z_l$에 남은 잔여 정보량
- $\beta$는 두 항 사이의 가중치로, 압축 정도를 결정하는 hyperparameter
이 최적화에서 $\lambda_l$를 크게 하면 $Z_l$가 $R_l$의 정보를 많이 포함하여 $I(R_l;Z_l)$가 커지지만, 너무 크게 하면 불필요한 정보까지 남아 $Z_l$와 $Y$의 관계 $I(Z_l;Y)$가 감소할 수 있다.
반대로 $\lambda_l$를 작게 하면 $Z_l$는 $R_l$와 공유 정보가 적어지지만 ($I(R_l;Z_l)$ 감소), 지나친 noise으로 인해 $Y$와 관련된 정보까지 잃어 $I(Z_l;Y)$가 줄어들 수 있다.
따라서 적절한 $\lambda_l$를 찾아 불필요한 부분은 노이즈로 대체하고 결정에 필수적인 부분만 유지하는 것이 IBA의 목표이다.
IBA를 통해 얻은 기여도 map은 $Z_l$에서 $\lambda_l$가 얼마나 1에 가까운지 에 따라 입력의 각 부분(픽셀 patch)의 중요도를 산출한다.
$\lambda_l$가 1에 가까울수록 해당 위치의 원본 특징 $R_l$가 유지되어 결정에 중요한 것으로 해석하며, 0에 가까울수록 불필요한 특징으로 간주된다.
이러한 방식으로 IBA는 ViT 내부 특정 한 layer에서 설명에 가장 유용한 정보를 추출하고, 이를 기반으로 입력 이미지의 중요한 영역을 설명한다.
Introduction
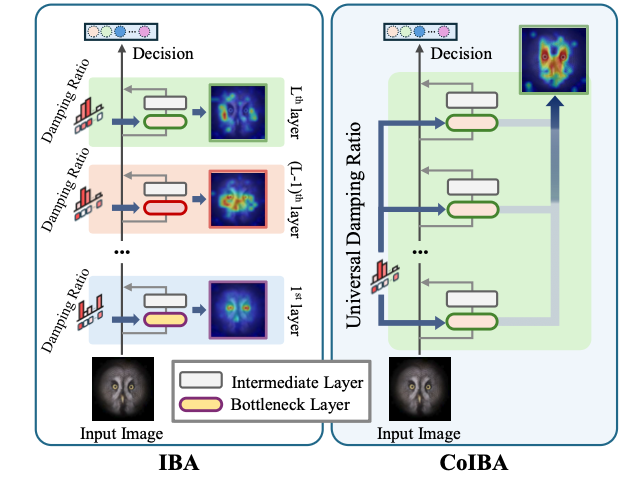
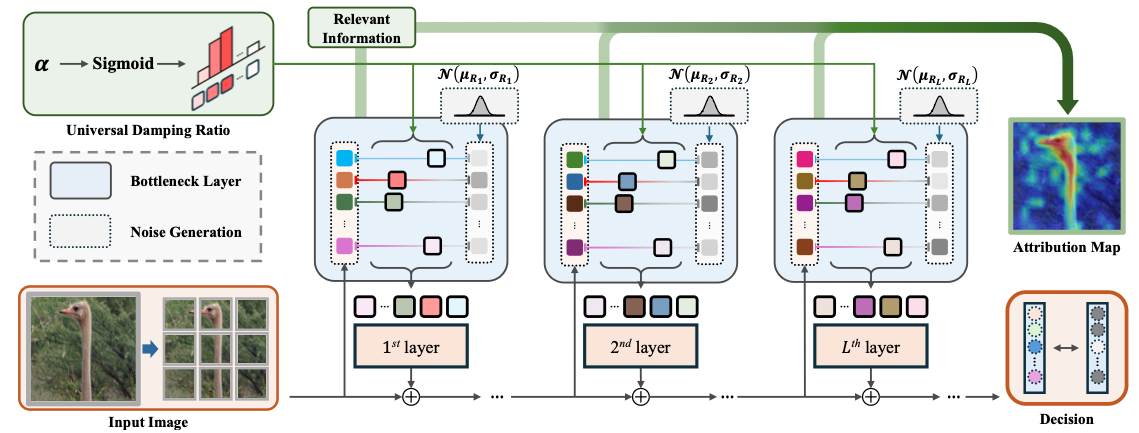
Comprehensive Information Bottleneck for Unveiling Universal Attribution (CoIBA)는 ViT의 의사결정 과정 전반에 걸친 근거를 밝히기 위해 다층에 정보 병목을 적용한 새로운 설명 기법이다.
이 논문은 기존 정보 병목 기반 방법(IBA)이 한 개의 layer에만 집중함으로써 발생하는 한계를 지적하고, 여러 layer에 걸친 종합적인 관련 정보를 추출함으로써 누락된 단서를 찾아내는 접근을 제안한다.
핵심 아이디어는 공통의 댐핑 비율을 여러 layer에 공유하여, 각 layer의 출력에서 중복되지 않는 유용 정보를 모두 모아 하나의 기여도 map으로 통합하는 것이다.
또한 서로 다른 layer들의 정보량을 균형 있게 고려하기 위해 변분(variational) 접근을 도입, 각 layer의 정보가 과도하게 압축되지 않도록 상호정보에 상한을 두었다.
이 방법을 통해 CoIBA는 이론적 보장 하에 “버려지는 활성값은 어떤 layer에서도 결정에 불필요한 정보”임을 확신하면서, 다층에 걸친 보편적 기여도를 산출한다.
다양한 실험 결과 CoIBA가 기존 기법 대비 높은 신뢰도의 설명을 제공함이 입증되었다 .
Goal
ViT 모델의 여러 계layer에 분산된 결정 근거를 모두 반영한 통합적인 특성 중요도 map을 생성하는 것
이를 통해 단일 layer 기반 설명의 누락된 부분을 보완하고, 더 신뢰할 수 있는 모델 해석을 실현하고자 한다 .
Motivation
기존 IBA는 한 layer의 정보만 활용해 설명을 제공하기 때문에, 결정 과정 전체의 증거를 놓칠 수 있다.
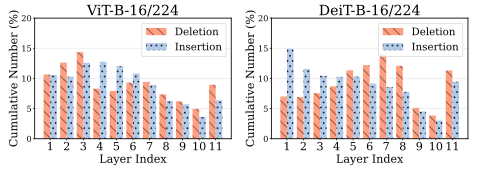
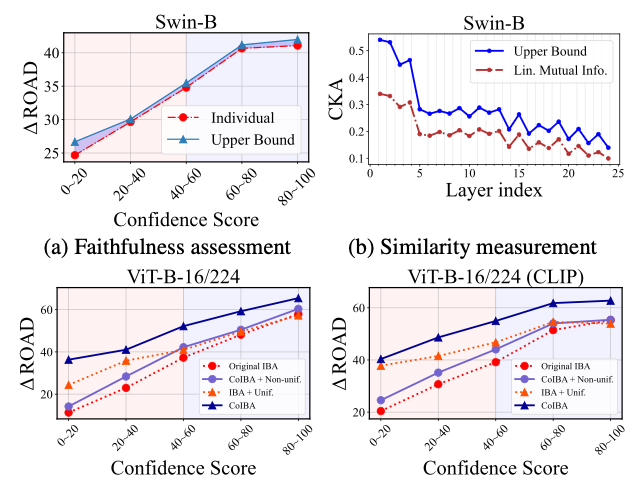
실제로 다양한 layer에서 얻은 기여도 map을 비교하면, 특정 한 layer이 항상 최적의 설명을 주지 못하며 (어떤 샘플에선 초기 layer, 다른 샘플에선 후반 layer이 더 중요한 정보 포함) 최적 layer이 샘플마다 다르게 분포한다.
위의 결과에서 각 샘플별 최고 성능을 내는 layer 번호가 고르게 분포하는데, 이는 설명을 위해 특별히 우수한 단일 layer이 존재하지 않는다는 사실을 보여준다.
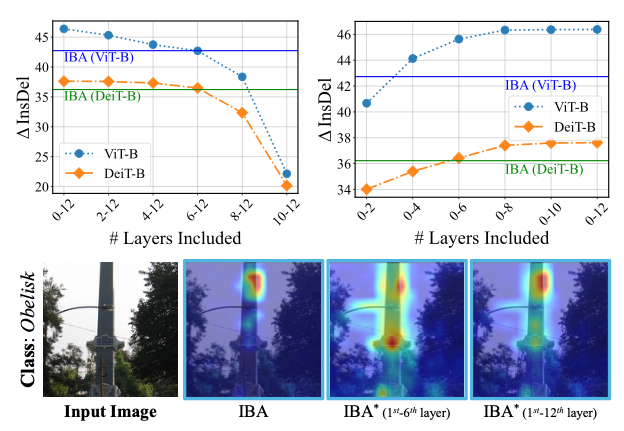
이러한 한계를 완화하기 위해 IBA를 여러 layer에 반복 적용하여 결과를 선형 결합하는 시도(IBA이라 명명)가 가능하나, 이는 연산 비용이 크고 향상 효과도 쉬운 사례에 국한되는 문제가 있다 .
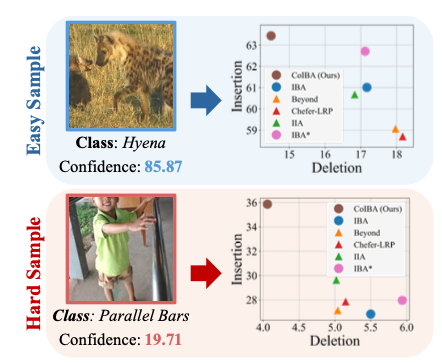
실제 IBA를 통해 얻은 성능 향상은 모델의 높은 신뢰 예측(easy)에서 주로 나타났으며, 낮은 신뢰 예측(hard)에서는 개선이 미미했다. 따라서 보다 효율적이면서 어려운 사례에도 강건한 다층 정보 통합 기법이 필요했다.
Contribution
CoIBA: 정보 병목을 다층에 도입하여 포괄적(feature-wise comprehensive)인 기여도 추정 기법을 제안
단일의 학습 파라미터(보편적 댐핑 비율)를 여러 layer에 걸쳐 공유
각 layer의 누락되었던 관련 정보를 서로 보완하여 최종 설명에 반영
이는 ViT 내부의 분산된 증거를 하나의 지도으로 통합하는 새로운 접근이다.
이론적 개선: 다층 정보 병목 적용 시 발생하는 layer별 상호정보 불균형 문제를 해결하기 위해 변분 상한(variational upper bound 방법을 도입
구체적으로, 첫 번째 layer의 상호정보로 다층의 총 상호정보를 상한으로 묶는 이론을 제시
이를 통해 다층 압축 항에 필요한 다수의 hyperparameter $\beta_l$를 단일 $\beta$로 단순화
이로써 모든 layer의 불필요한 정보는 제거되면서도, 각 layer의 유용한 정보는 공정하게 반영되도록 보장
향상된 설명 성능: CoIBA를 ViT (및 Swin Transformer 등) 다양한 모델과 데이터셋에 적용한 결과, 기존 기법 대비 높은 설명 충실도(faithfulness)를 보였다.
- Insertion/Deletion, ROAD, FunnyBirds 등 다각적인 평가에서 CoIBA의 기여도 map은 모델 예측에 더 큰 영향력을 지닌 것으로 나타남
- 특히 기존 IBA가 간과한 대비성(contrastivity) 측면에서 뛰어난 성능
- 더불어 어려운 입력 샘플(모델이 불확실한 예측)에 대해서도 일관된 품질을 유지함을 확인
Method
Background – IBA (기존 정보 병목 설명 기법)
다시한번 기존 IBA 방법을 자세히 살펴보자.
IBA는 앞서 배경에서 소개했듯, 한 개의 특정 중간 layer $l$에 Bottleneck을 삽입하여 해당 layer의 관련 정보(relevant information)를 추출한다.
$R_l$을 $l$번째 layer의 원본 활성값(representation), $Z_l$을 Bottleneck을 통과한 출력 representation이라 하면,
\[Z_l = \lambda_l R_l + (1 - \lambda_l),\epsilon_l \tag{1}\]로 $Z_l$을 정의한다. 여기서 $\lambda_l$ (0부터 1 사이)은 학습되는 댐핑 비율이고, $\epsilon_l$은 $R_l$과 동일한 분포를 갖도록 한 독립 가우시안 noise이다.
이 Bottleneck 변수 $Z_l$는 $R_l$의 정보를 부분적으로만 포함하므로, $\lambda_l$ 값을 조절하여 얼마나 정보를 남길지 결정할 수 있다.
IBA의 objective function는 $Z_l$이 레이블 $Y$와 최대한 많은 정보를 가지면서도 $R_l$과의 불필요한 공유정보는 최소화하도록 설정된다. 즉,
\[\max_{\lambda_l} I[Z_l; Y]-\beta,I[R_l; Z_l] \tag{2}\]를 만족하는 $\lambda_l$를 찾는다.
$I[Z_l;Y]$는 Bottleneck 출력과 정답 사이의 관련성(relevancy)을 나타내며, $I[R_l;Z_l]$는 Bottleneck이 통과시킨 잔여 정보량(compression)을 의미한다.
$\beta$는 두 항 사이의 가중치로 주어지는 트레이드오프 계수이다.
이 식을 최대화하면, $\lambda_l$가 커져 $Z_l$에 담긴 예측 관련 정보 $I[Z_l;Y]$가 증가하는 방향으로 학습되지만, 동시에 $\lambda_l$가 너무 크면 $R_l$의 불필요한 정보까지 $Z_l$에 남아 $I[R_l;Z_l]$이 커지므로 패널티를 받는다.
결과적으로 $\lambda_l$가 적절한 값으로 최적화되어 $Z_l$는 $Y$에 필요한 정보만 간직하게 된다.
이때 $I[Z_l;Y]$의 직접 계산은 어려우므로, 실험에서는 $Z_l$로 모델 출력 $\hat{Y}$를 다시 예측하는 크로스 entropy loss을 최소화하는 것으로 대체하여 $\lambda_l$를 학습시킨다.
이렇게 얻은 $\lambda_l$ (patch별 스칼라값들의 모음)는 입력 이미지의 각 patch 기여도를 의미하며, 이를 시각화하면 해당 레이블에 대한 중요도 map이 된다.
IBA는 ViT뿐 아니라 일반 CNN 등에도 적용될 수 있는 기법으로, 특정 layer 하나만을 사용해 부분적인 설명을 제공해왔다.
그러나 다음 절에서 보듯 이 방법은 결정 과정의 모든 단서를 포착하지 못하는 한계가 있다 .
Motivation
IBA가 한 layer의 정보만으로 기여도를 추론하다 보니, 결정 근거가 분산된 ViT의 특성상 일부 단서가 누락될 수 있다.
특정 한 layer만으로는 항상 충분한 설명을 제공할 수 없으며, 결정 과정의 증거들이 여러 layer에 걸쳐 흩어져 있음을 위 그래프에서 알 수 있다.
그렇다면 여러 layer의 정보를 결합하면 나은 설명을 얻을 수 있을 것이다.
이를 위해 저자들은 IBA를 전 layer에 순차적으로 적용한 후 각 layer의 기여도 map을 선형 결합하는 실험을 진행하였다.
이렇게 얻은 방법을 IBA*로 명명하고 성능을 비교한 결과, 단일 layer IBA 대비 성능 향상이 관찰되었다.
특히 삽입/삭제 점수에서 IBA*가 IBA보다 높게 나타나, 여러 layer의 관련 정보를 합치면 설명의 신뢰도가 향상됨을 보였다.
그러나 추가 분석에서 이 향상은 쉽게 예측할 수 있는 샘플(easy)에 국한되고, 모델이 자신 없어하는 어려운 샘플(hard)에서는 IBA도 IBA와 큰 차이가 없었다.
위는 예측 신뢰도 점수에 따라 IBA와 IBA*의 성능 차이를 분리해 보여주는데, 높은 신뢰구간(confidence)에서는 개선이 크지만 낮은 신뢰구간에서는 미미함을 확인할 수 있다.
이는 단순 합산 방식으로는 여전히 layer 간 정보 활용의 비효율이 존재함을 시사한다.
아울러 IBA는 모든 layer에 대해 $\lambda_l$를 개별 최적화하므로 계산 비용이 배로 증가하는 실용적 문제도 있다.
요컨대, 다층 정보를 효율적으로 통합하면서도 난이도에 상관없이 일관된 설명 성능을 내는 방법이 필요하다는 것이 CoIBA 개발의 동기가 되었다.
Comprehensive Information Bottleneck (CoIBA)
CoIBA는 ViT의 여러 중간 layer들에 동시에 Bottleneck을 삽입하여 정보 흐름을 제어하고, 각 layer에서 의미있는 정보를 모두 추출해내는 방법이다.
IBA가 한 위치에서 국소적으로 정보를 제한했다면, CoIBA는 다수의 지정한 layer들(targeted layers)에 IB를 적용함으로써 전체 의사결정 경로를 설명하고자 한다.
특히 보편적(universal) 댐핑 비율 $\lambda$를 도입한 것이 큰 차별점인데, 이는 여러 layer에 공통으로 적용되는 단일 제어변수이다. 각 layer마다 개별 $\lambda_l$를 쓰는 대신, 모든 Bottleneck에 동일한 $\lambda$를 사용함으로써 layer들 사이에 정보 공유가 가능해진다.
한 layer에서 너무 많이 압축되어 누락된 결정 단서도, 다른 layer에서 관련 정보를 전달받아 보완될 수 있다는 것이다. 결과적으로 CoIBA의 Bottleneck들은 연결된 형태로 동작하며, 어떤 layer에서도 중요 정보가 과도하게 버려지지 않도록 상호 보완적인 역할을 한다.
Formulating Information Restriction
CoIBA에서는 입력 이미지 $X$를 거쳐 일련의 중간 representation들이 생성되는 ViT의 계층 구조에 Bottleneck을 삽입한다.
예를 들어 $s$번째부터 $e$번째까지 총 $L = e-s+1$개의 layer를 선택했다면, 이들 각 layer 앞에 Bottleneck 연산이 들어간다.
순서를 따라 $Z_0, Z_1, …, Z_L$로 Bottleneck 변수를 정의하면, $Z_0$는 첫 Bottleneck이 삽입되는 layer 직전의 비Bottleneck representation이며 (즉 $Z_0 = R_s$로 놓음), $Z_L$은 마지막 Bottleneck 후의 출력이다.
각 Bottleneck layer에서, 이전 layer의 출력 $Z_{l-1}$을 입력으로 받아 현재 layer의 원래 활성값 $R_l$을 계산한다 (이를 $R’_l$이라 하자). 그리고 IBA와 마찬가지로 가우시안 noise $\epsilon_l$을 주입해 $Z_l$을 얻는다.
다만 공통 댐핑 비율 $\lambda$를 쓰므로, 모든 layer에서 동일한 $\lambda$로 $R’_l$을 감쇠시킨다:
\[Z_l = \lambda,R’_l + (1 - \lambda),\epsilon_l \tag{3}\]모든 $l$-번째 Bottleneck layer에 대해 $\lambda$는 동일하며, $\lambda$ 값 하나가 전체 Bottleneck들의 개방 정도를 제어한다.
여기서 $\lambda$는 $\mathbb{R}^{P\times 1}$ 벡터로 정의되며 ($P$: patch 개수), 각 입력 patch token별로 하나씩의 값을 갖는다.
즉 이미지의 patch마다 중요도가 다르게 적용될 수 있으나, 채널 차원(token의 embedding 차원)에는 일괄적으로 동일한 $\lambda$가 적용된다.
이렇게 함으로써 서로 다른 채널(feature)마다 상이한 계수를 두지 않고, token(공간 위치)별로 일관된 중요도 판단을 하도록 하였다.
저자들은 채널 전체에 균일한 감쇠를 주는 것이 오히려 token의 중요도 집중에 도움이 되어 설명 성능을 향상시킨다고 보고하였다.
참고로 $\lambda$는 sigmoid 함수로 매핑된 학습 파라미터 $\alpha$로 구현되는데, 초기값을 5로 설정하여 $\lambda \approx 0.99$로 시작함으로써 처음에는 정보 loss이 거의 없도록 하였다. 이후 학습을 통해 $\lambda$가 점진적으로 조정되며 각 patch의 중요도가 드러나게 된다.
Information Bottleneck Objective
다층 Bottleneck의 목표는 모든 Bottleneck layer에서 관련 정보를 추출하는 것이다.
이를 위해 CoIBA는 IBA의 식 (2)을 다층으로 확장한다.
여러 layer에 Bottleneck을 넣었으므로 압축 항은 각 layer별 $I[Z_{l-1}; Z_l]$의 합으로 표현된다.
최종 (마지막 Bottleneck 출력 $Z_L$와 레이블 $Y$ 간) 관련성 항은 $I[Z_L; Y]$로 그대로 쓴다. 따라서 CoIBA의 다층 정보 병목 최적화는 다음과 같다:
\[\underset{\lambda}{\max}\; I[Z_{L};Y]-\frac{1}{L}\left(\sum_{l=1}^{L}\beta_l,I[Z_{l-1};Z_l]\right). \tag{4}\]- $I[\cdot;\cdot]$: 상호정보
- $Z_l$: $l$번째 Bottleneck의 출력 representation
- $Z_0=R_1$: 첫 Bottleneck이 삽입된 layer의 원래 중간 representation
- $Y$: 정답(ground truth
- $\lambda$: 패치별 댐핑 비율(Bottleeneck이 원 신호를 얼마나 통과시킬지 제어)
- $\beta_l$: layer 별 압축 강도(trade-off 제어)
- $L$: Bottleneck을 넣은 layer 개수
해석하면, $I[Z_L;Y]$를 키워 예측에 필요한 정보를 최대 보존하고, ${I[Z_{l-1};Z_l]}$의 합을 줄여 연속된 내부 representation들 사이의 잉여 공유정보를 억제한다. 앞의 $1/L$은 Bottleneck을 몇 layer에 넣었는지에 따른 규모 효과를 정규화해, layer 수가 늘어나도 패널티가 과도해지지 않도록 한다.
실무 최적화에서 $I[Z_L;Y]$ 직접 계산은 어렵기 때문에, 분류 손실을 최소화하여 대체한다: \(\max I[Z_L;Y]\Longleftrightarrow\min \mathcal{L}_{ce}(f(Z_L),Y).\)
- $\mathcal{L}_{ce}$: 크로스트로피 손실
- $f(\cdot)$: Bottleneck 출력을 받아 예측을 만드는 모델(헤드)
이를 통해 $\lambda$ (공유 파라미터 벡터)가 학습되면, 최종적으로 각 patch의 값 $\lambda_i$ (0~1 사이)가 해당 patch의 중요도 점수가 된다.
이 점수들은 여러 layer의 정보를 종합하여 계산되므로, CoIBA의 기여도 map은 의사결정 전반에 대한 통합적인 설명을 제공한다.
각 layer마다 $\beta_l$ (양수의 hyperparameter)을 두어, layer별 압축-관련성 균형을 조절할 수 있게 하였다.
다만 $\beta_l$ 값 설정은 매우 까다로운 작업인데, 이상적인 $\beta_l$를 찾기 위해서는 각 layer의 중요도를 사전에 알아야 하는 모순이 있다.
layer이 깊어질수록 일반적으로 $I[Z_{l-1};Z_l]$가 작아질 것이나, 정확한 분포나 감소율을 예측하기 어렵기 때문에 $\beta_l$들을 적절히 정하는 것은 힘들다.
이 때문에 기존 접근으로 다층 IB를 적용하면 광범위한 험난한 탐색(heuristic search)을 해야 한다고 지적한다.
CoIBA에서는 이를 극복하기 위한 해결책을 다음 절(Variational Upper Bound)에서 제시한다.
KL
내부 상호정보는 KL 발산으로 쓴다:
\[I[Z_{l-1};Z_l]=\mathbb{E}_{Z_{l-1}}\left[D_{\mathrm{KL}}\big(P(Z_l\mid Z_{l-1})\|P(Z_l)\big) \right]. \tag{5}\]하지만 $P(Z_l)=\int_{Z_{l-1}} P(Z_l\mid Z_{l-1})P(Z_{l-1})\;dZ_{l-1}$ 은 적분 때문에 직접 추정이 난해하다.
그래서 가우시안 근사 사전 $Q(Z_l)$을 둔다:
\[Q(Z_l)=\mathcal{N}\big(\mu_{R_l},\sigma_{R_l}^2\big),\]- $\mu_{R_l},\sigma^2_{R_l}$: 보틀넥 없이 같은 layer 원표현 $R_l$의 평균/분산
이때 다음 upper bound를 얻는다:
\[I[Z_{l-1};Z_l]\le\mathbb{E}_{Z_{l-1}}\left[D_{\mathrm{KL}}\big(P(Z_l\mid Z_{l-1})\|Q(Z_l)\big)\right]. \tag{6}\]- 가우시안 $Q(Z_l)$을 쓰면 실제 $P(Z_l)$보다 과대평가(upper bound)가 된다.
- 따라서 우변을 최소화하면 실제 $I[Z_{l-1};Z_l]$도 함께 줄어드는 보수적(안전한) 압축이 달성된다.
- 구현 측면에서 우변은 모수화/샘플링이 가능하여 안정적으로 최적화된다.
왜 “연속된 $I[Z_{l-1};Z_l]$의 합”인가
Description
보틀넥이 layer 순서대로 삽입되므로, 정보가 $Z_0\to Z_1\to\cdots\to Z_L$로 전달될 때 각 단계의 공유정보가 누적된다. 합 $\sum_l I[Z_{l-1};Z_l]$에 패널티를 주면,
특정 한 layer에서만 정보가 과도하게 남거나(누수)
앞쪽에서 지워진 유용 정보가 뒤에서 왜곡되어 보상되는
현상을 억제하며, 전체 경로의 잉여 정보를 일관되게 줄인다. $\beta_l$은 layer별로 이 패널티 강도를 조절한다.
구현 관점 요약
- 관련성 극대화: $I[Z_L;Y]\uparrow \;\; \Rightarrow \; \mathcal{L}_{ce}(f(Z_L),Y)\downarrow$
- 압축 최소화: $\sum_l \beta_l,I[Z_{l-1}Z_l]\downarrow \;\;\Rightarrow$ KL-상계(식 3) 최소화
- 정규화: $\frac{1}{L}$ 로 layer 수 의존성 완화
- 초깃값과 안정성: $Z_0=R_1$로 두어 첫 보틀넥 이전 표현을 기준 삼고, $Q(Z_l)$을 $R_l$ 통계에 맞춘 가우시안으로 두어 분포 불일치를 줄인다.
한눈에 보는 직관
- $I[Z_L;Y]$는 “예측에 꼭 필요한 정보가 마지막 보틀넥을 통과했는가?”를 측정한다.
- $I[Z_{l-1};Z_l]$는 “연속된 두 보틀넥 사이에 얼마나 정보가 남아 돌고 있는가(중복/잡음 포함)?”를 본다.
- 결과적으로, 중요한 건 남기고, 중요하지 않은 건 단계별로 덜어내는 소프트-마스킹을 학습하게 된다(댐핑 비율 $\lambda$가 그 역할을 수행).
Variational Upper Bound (변분 상한 적용)
CoIBA의 핵심 개선 중 하나는 다층 Bottleneck의 압축 항을 하나의 상한으로 묶은 것이다.
저자들은 다음 두 가지 사실에 주목한다.
- Bottleneck을 거치든 안 거치든 모델 입력과 출력 간의 상호정보가 모든 내부 layer의 상호정보보다 크거나 같다.
- 이는 정보 경로상 추가 정보는 생기지 않기 때문
- 데이터 처리 부등식에 의해 $I[X;Z_l] \ge I[X;Z_{l+1}]$
- 뒤쪽 layer의 상호정보는 앞쪽 layer보다 작거나 같다
- 연속적인 noise 주입**은 내부 representation의 상호정보를 점층적으로 감소시키기 때문
- $I[Z_{l-1};Z_l] \ge I[Z_l;Z_{l+1}]$
이 두 가지를 결합하면, 첫 Bottleneck과 마지막 Bottleneck 사이의 모든 상호정보의 합이 첫 Bottleneck 입력이 가진 정보의 $L$배보다 클 수 없다는 상계를 얻을 수 있다 :
\[I[R_1; Z_1] \ge \frac{1}{L}\sum_{l=1}^{L} I[Z_{l-1}; Z_l] \tag{7}\]여기서 $R_1$은 선택한 Bottleneck 구간의 첫 layer 입력 (즉 $Z_0$)이고 $Z_1$은 그 Bottleneck 출력이다.
이 부등식은 “여러 layer에 분산된 불필요한 정보의 총량도 결국 첫 layer에서 기인한 것 이상이 될 수 없다”는 의미로 해석된다.
이를 이용하여 압축 항의 상한을 $;I[R_1;Z_1]$ (첫 layer의 상호정보)로 묶을 수 있다.
즉, 개별 $\beta_l$을 둘 필요 없이 단일 $\beta$로 첫 layer의 상호정보만 조절하면 나머지 layer들도 함께 제한할 수 있다는 것이다.
이렇게 하면 식 (4)는 다음과 같이 단순화된다 :
\[\max_{\lambda} I[Z_L; Y]- \beta I[R_1; Z_1] \tag{8}\]이 변형된 목적식에서는 $\beta$ 하나만 튜닝하면 되므로, 다층 정보 병목의 hyperparameter 부담이 크게 줄어든다.
또한 중요한 효과로, Bottleneck 압축을 첫 layer에 대해서만 계산하면 되므로 나머지 layer의 $I[Z_{l-1};Z_l]$를 일일이 평가할 필요가 없다.
첫 layer의 상호정보 $I[R_1;Z_1]$는 $R_1$ (non-perturbed 입력)과 $Z_1$ (첫 Bottleneck 출력) 간의 값으로, 해당 layer의 $R_1$과 가우시안 근사 $Q(Z_1)$를 써서 이전처럼 계산하면 된다.
이렇게 함으로써 계산량이 감소하고, 상호정보 추정의 일관성도 유지된다.
이론적 이득
식 (8)의 형태는 IBA의 식 (2)와 유사해 보이지만, 사실 큰 이점을 지닌다.
IBA는 특정 병목 삽입 계층에서 관련 정보를 획득한다.
따라서 계층별 기여도 지도를 얻으려면 반드시 계층을 반복적으로 실행해야 한다.
반면 CoIBA는 보편적인 감쇠 비율을 사용하여 각 병목 삽입 계층으로부터 계층별 관련 정보를 탐색한다.
IBA에서는 특정 layer 하나만 고려하므로, 만약 초기 layer에 Bottleneck을 넣으면 그 layer의 $I[R_l;Z_l]$를 크게 줄여야 해 $\beta$ 값에 따라 과도한 정보 loss이 발생할 수 있다.
반면 CoIBA의 식 (8)은 여러 layer의 합을 첫 layer으로 묶었기에, 앞쪽 layer에서의 정보 과소평가 문제가 완화된다.
이는 뒤쪽 layer들의 관련 정보가 앞쪽 layer으로 보정(compensation)되어 전달되기 때문이다.
결과적으로 CoIBA는 각 layer의 관련 정보가 공정하게 반영될 수 있는 토대를 마련한다.
다시 말해, $\beta$ 값 하나로 모든 layer의 불필요한 정보를 제약하면서도 필요한 정보는 각 layer에서 누락 없이 합산되도록 보장하는 것이다.
이러한 이론적 개선을 통해 CoIBA는 모든 타겟 layer에서 불필요한 활성값은 실제로 예측에 불필요함을 보장할 수 있다. 이는 곧 CoIBA 기여도 map의 신뢰성을 뒷받침하는 요소다.
Overview
요약하면, CoIBA의 방법론적 구성은 다음과 같다.
- 우선 ViT의 여러 layer에 Bottleneck을 삽입하고 하나의 $\lambda$로 정보를 제어
- 식 (8)의 목표를 최적화하여 $\lambda$ 값을 학습
- 학습 시 각 Bottleneck의 압축 항들은 첫 Bottleneck의 상호정보로 상한이 걸려 일괄 제어되며, 관련성 항은 마지막 출력과 레이블 간 cross-entropy로 대체되어 계산
- 학습된 $\lambda$ 벡터는 입력 patch들의 통합 중요도로 해석되어 기여도 map을 형성
- CoIBA는 정보 흐름을 제한하여 각 layer의 관련 정보만 남긴 뒤, 그것들을 종합
- 하나의 기여도 map으로 산출
Experiments
4.1. Setup (실험 설정)
모델 및 데이터셋
저자들은 다양한 ViT 계열 모델을 사용하여 CoIBA의 성능을 평가하였다.
- ViT 원본 모델들 (Ti/16, S/16, B/16, L/16, H/14 등 크기별)
- 파생인 DeiT-S/B, 최신 DeiT3-L 등
총 8종의 Transformer를 실험에 포함시켰다.
이들 중 일부는 ImageNet-21k로 pre-training되었고, 소형 모델들은 strong regularization 기법으로 학습된 버전(ViT, DeiT)도 포함되었다.
추가로 Swin Transformer(Swin-B, Swin2-B)도 실험에 추가하여, CoIBA가 다중 스케일 특성을 지닌 ViT에도 적용 가능함을 보였다.
실험 데이터셋으로는 ImageNet-1k (IN-1k) 검증 세트를 주로 사용하고, 모델 일반화 성능을 살펴보기 위해 ImageNet-A (IN-A) 및 ImageNet-R (IN-R) 어려운 샘플 집합도 사용하였다.
IN-A와 IN-R은 각각 이상치나 스타일 전환 등 분포가 달라 모델이 오분류하기 쉬운 이미지들로 구성되어, 난이도별 분석에 활용되었다 .
비교군
CoIBA의 성능을 평가하기 위해 다양한 ViT 설명 기법들과 비교하였다.
- Propagation-based 방식
- Chefer-LRP (ViT 전용 LRP)
- Generic Attention 모델 (다목적 Transformer 설명)
- IIA (Iterated Integrated Attentions)
- ViT-CX (token 연결 구조 고려)
- Beyond (token 중요도 재해석)
- Information-based 방식
- 기존 IBA
- 저자들이 구현한 IBA* (동일 조건에서 다층 반복 IBA)
각 방법은 저자들이 공개한 코드 및 설정을 따랐으며, 특히 IBA는 $\beta=10$으로 두고 ViT-B 모델 기준 6번째 layer에 Bottleneck을 넣어 수행하였다.
반면 CoIBA는 $\beta=1$로 설정하고, ViT-B의 경우 4번째부터 12번째까지 (즉 마지막 클래스 token 직전까지) 모든 layer에 Bottleneck을 삽입하여 사용하였다.
최적화는 learning rate 1, 배치사이즈 10, Adam optimizer 등으로 설정하여, 각 입력에 대한 $\lambda$를 학습한다.
(CoIBA는 테스트 시 매 입력 이미지마다 $\lambda$를 최적화하여 해당 이미지의 기여도 map을 산출하는 방식이다. 이는 IBA와 동일한 프로토콜이다.)
Swin Transformer의 경우 구조적 차이로 인해, 방법론 수정 없이 적용 가능한 일부 기법(Generic, ViT-CX, IBA, Beyond, CoIBA)만 비교에 포함하였다.
4.2. FunnyBirds Assessment
FunnyBirds 실험 은 기존 이미지에 인공적 새(bird) patch를 삽입하여 해당 위치가 타겟 클래스에 얼마나 중요한지를 평가하는 프레임워크다.
각 이미지에는 사람에 의해 레이블된 ground truth box가 있는데, 이는 모델이 집중해야 할 영역이다.
이 데이터셋을 통해 생성된 기여도 map의 정확성을 3가지 측면에서 평가한다
- 완전성(completeness) – 중요한 영역을 충분히 포착했는가
- 정확성(correctness) – 강조한 픽셀이 실제 타겟과 관련있는가
- 대비성(contrastivity) – 타겟 클래스에 특화된 중요한 부분을 잘 구별했는가
를 측정한다.
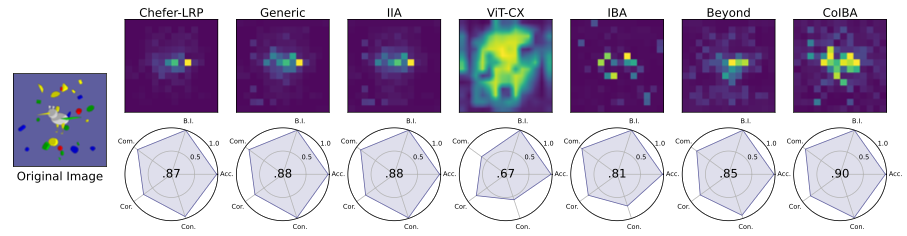
위는 FunnyBirds 실험에 대한 정량 및 정성 평가 결과를 보여준다.
CoIBA로 생성한 기여도 map은 모든 기준에서 기존 기법들을 능가하였으며, 특히 propagation 계열(Chefer-LRP, Generic, IIA 등)뿐 아니라 정보이론 계열(IBA 등) 모두보다 우수한 점수를 기록했다.
흥미로운 점은 CoIBA가 기존 IBA 대비 대비성을 크게 향상시켰다는 것이다.
IBA는 타겟 클래스와 상관없는 영역도 어느 정도 강조하는 경향이 있었는데, CoIBA는 다층 정보 활용 덕분에 타겟에 특화된 단서를 부각하여 불필요한 배경 강조를 줄였다고 서술한다.
이러한 결과는 CoIBA가 보다 인간이 이해하기 쉬운, 명확한 근거를 제공함을 의미한다.
(Fig. 6 중앙의 Radar Chart 형태 그래프에서 CoIBA는 모든 축에서 높은 수치를 보여, 종합 스코어 면에서도 탁월함을 입증한다.)
4.3. Insertion/Deletion
삽입/삭제 평가는 기여도 map의 정확성(correctness)을 확인하는 대표적인 방법이다.
- 삭제(deletion)
- 기여도 map에서 중요하다고 표시된 픽셀들을 순차적으로 masking하여 모델 예측 확률이 얼마나 떨어지는지 관측
- 삽입(insertion)
- 중요 픽셀들만 점진적으로 원본 이미지에 남겨두고 나머지는 masking하여 예측 확률이 얼마나 회복되는지 측정
두 경우 모두 AUC (Area Under Curve) 점수를 사용하며, 삽입은 클수록, 삭제는 작을수록 기여도 map이 정확하게 핵심 픽셀들을 짚었다는 뜻이 된다.
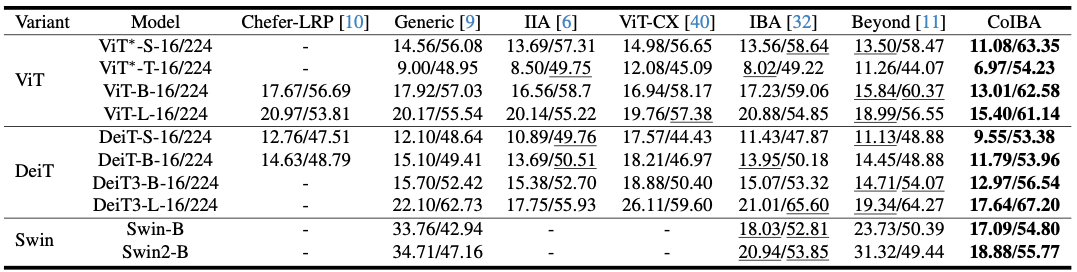
위는 여러 모델에 대해 CoIBA와 기존 기법들의 삽입(↑)/삭제(↓) 점수를 비교한 결과이다.
각 셀의 왼쪽 값이 삭제 후 남은 모델 accuracy(낮을수록 좋음), 오른쪽 값이 삽입 후 모델 accuracy(높을수록 좋음)를 의미한다.
전반적으로 CoIBA는 모든 모델에서 가장 우수한 삽입/삭제 점수를 기록하였다.
표에서 밑줄이 기존 기법들 중 SOTA인데, CoIBA의 점수는 이를 뛰어넘는다
예를 들어 ViT-B/16의 경우 CoIBA 적용 시 삭제 후 accuracy가 13.01%로 가장 낮고, 삽입 후 accuracy는 62.58%로 가장 높아, 가장 중요한 픽셀들을 정확히 찾아냈음을 보여준다.
DeiT-B, ViT-L 등 다른 모델들도 유사한 경향을 보이며, 특히 대형 모델일수록 CoIBA의 상대적 개선이 두드러진다
이는 모델이 깊고 복잡할수록 다층 설명의 이득이 크다는 의미
이 실험은 CoIBA의 기여도 map이 실제로 모델의 예측 결정에 영향력이 큰 부분들을 정확히 식별하고 있음을 뒷받침한다.
4.4. Remove and Debias (ROAD)
기여도 map 평가 시 단순 삭제의 한계를 보완한 지표이다.
삭제 평가는 중요한 픽셀을 지울 경우 모델 출력 변화량을 보지만, mask의 형태가 모델에 새로운 힌트를 주는 문제(예: 특정 모양으로 가려진 공백이 힌트가 될 수 있음)가 있다.
ROAD는 이러한 클래스 정보 누설(leakage)를 막고자, 중요 영역을 제거할 때 대조 클래스에 속하는 patch로 교체하거나 입력 분포를 보존하는 방식으로 디바이싱한다.
이때 MoRF(Most Relevant First)와 LeRF(Least Relevant First) 두 가지 관점을 모두 본다.
- MoRF는 가장 중요한 부분부터 제거하면서 모델 성능 하락을 측정
- LeRF는 가장 덜 중요한 부분부터 제거하면서 성능을 측정
좋은 기여도 map일수록 MoRF 시 성능이 크게 떨어지고 (중요한 걸 지웠으니 모델이 망가짐), LeRF 시 성능이 천천히 떨어진다 (중요하지 않은 걸 지웠으니 영향 적음).
각 셀의 왼쪽이 MoRF (↓ 낮을수록 좋음), 오른쪽이 LeRF (↑ 높을수록 좋음) 점수이다.
결과를 보면, 모든 경우에서 CoIBA의 ROAD 성능이 가장 우수하다.
예를 들어 ViT-B/16에서 CoIBA는 MoRF 16.63% (가장 낮음), LeRF 73.68% (가장 높음)으로, 다른 방법들을 크게 앞선다.
DeiT-B, ViT-L 등에서도 CoIBA는 MoRF를 최소화하고 LeRF를 최대화하여, 중요 픽셀과 비중요 픽셀을 가장 잘 구별함을 보여준다.
ROAD 실험은 CoIBA 기여도 map이 클래스에 특화된 정보를 잘 포착하고, 중요하지 않은 배경은 덜 부각시키는 균형 잡힌 설명을 제공함을 시사한다.
4.5. Difficulty-aware Correctness Assessment
CoIBA의 성능이 입력 난이도(모델 확신도)에 따라 일관된지를 분석하기 위해, 저자들은 난이도별 평가를 수행하였다.
먼저 각 데이터셋 (IN-1k, IN-A, IN-R)의 모든 샘플에 대해 모델의 예측 신뢰도(softmax score) 분포를 구하고, 이를 구간별(예: 020%, 2040%, …, 80~100%)로 나누었다. 그런
다음 앞선 Insertion/Deletion 및 ROAD 지표에서, 해당 난이도 구간별로 CoIBA와 타 기법들의 성능을 비교했다.
이는 이러한 난이도별 성능을 시각화한 그래프로, 좌측 (a)는 IN-1k, (b)는 IN-A, (c)는 IN-R에 대한 결과이다.
그래프에서 가로축은 신뢰도 구간, 세로축은 지표 점수 변화를 나타낸다. 빨간 실선이 CoIBA이고, 나머지 기법들은 점선 등으로 표시되었다.
결과를 보면, 모든 난이도 구간에서 CoIBA가 가장 우수한 성능을 유지하는 것을 알 수 있다.
특히 IN-A나 IN-R과 같이 어려운 샘플이 많은 세트의 경우, CoIBA와 다른 기법 간 격차가 더욱 벌어졌다.
이는 CoIBA가 난이도가 높아도 정보 결합을 통해 더 나은 설명을 만들어내는 강인함을 보여준다.
저자들은 IN-A, IN-R 결과가 CoIBA의 우수한 어려운 샘플 처리 능력을 뒷받침한다고 언급했다.
요컨대, CoIBA는 쉽든 어렵든 일관되게 높은 설명 정확성을 유지하여, 특정 조건에서만 좋은 것이 아닌 전반적으로 신뢰할 수 있는 기법임을 입증하였다.
4.6. Discussion
Ablation on Bottleneck-inserted Layers
저자들은 CoIBA에서 몇 개 layer을 포함시켜야 최적인지를 실험적으로 검증했다.
ViT-B 모델을 대상으로, Bottleneck을 다양한 범위의 layer에 삽입하면서 Insertion/Deletion 성능을 비교하였다.
예를 들어 2-12layer, 4-12layer, 6-12layer, 8-12layer 등 출발 layer(s)과 도착 layer(e)을 달리하며 CoIBA를 적용하고 결과를 측정했다.
(a), (b)를 보면 포함 layer 수가 늘어날수록 성능이 꾸준히 향상되었다.
특히 8-12 layer (뒷부분 5개 layer)만 사용할 때보다 4-12 layer (초기 4 layer부터 전부) 사용할 때 Insertion 점수가 더 높고 Deletion 점수가 더 낮아져, 초반 layer 정보까지 통합하는 편이 설명 성능에 이롭다는 결론을 얻었다.
더 나아가 CoIBA는 동일 조건에서 IBA*보다 큰 차이로 우수했는데, 한 번의 최적화로도 IBA*의 다중 반복을 뛰어넘는 성능을 달성했음을 보여준다.
이는 CoIBA의 효율적 설계(공유 $\lambda$ 및 변분 상한)가 실제로 효과적임을 검증하는 증거다.
결과적으로 다층을 적극 활용할수록 그리고 CoIBA의 통합 방식으로 활용할 때 설명 성능이 향상됨을 알 수 있었다.
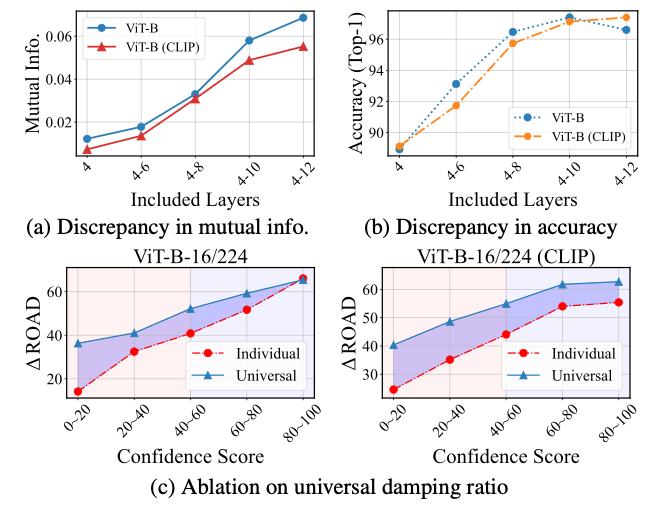
Effectiveness of Universal Damping Ratio
CoIBA의 중요한 설계 요소인 보편적 $\lambda$ 적용이 성능에 미치는 영향을 분석하였다.
동일한 다층 설정에서, 각 layer별로 $\lambda_l$를 따로 두는 경우와 단일 $\lambda$를 공유하는 경우를 비교한 것이다.
위 (c)에 그 결과가 제시되어 있는데, 공유 $\lambda$를 쓴 경우가 개별 $\lambda$ 대비 Insertion/Deletion 성능이 더 높았다.
또한 (a)에서 $\lambda$ 공유 시 초기 layer의 mutual info 감소량이 적어 (과잉 압축 보완) 뒤로 갈수록 더 많은 관련 정보가 증폭되는 경향을 보였고, (b)에서도 최종 예측 accuracy가 더 높게 나타났다.
이는 보편적 댐핑 비율이 초기layer 정보 loss을 보충하고 관련 정보 전달을 증폭시키는 역할을 함을 의미한다.
결과적으로 개별 $\lambda$ 대비 공유 $\lambda$ 체계가 CoIBA의 설명 accuracy를 향상시키며, 설계 의도가 옳았음을 확인하였다 .
Effectiveness of Variational Upper Bound
마지막으로, 제안한 Variational Upper Bound (Eq. (8))이 실제 성능에 미치는 영향을 검증하였다.
이를 위해 $\beta_l$를 사용한 기존 다층 IB 방식(Eq. (4))과, $\beta$ 하나로 단순화한 CoIBA 방식(Eq. (8))을 비교하였다.
(a)에 따르면, CoIBA의 상한 적용 방식이 난이도 구간을 막론하고 삽입/삭제 accuracy를 높이는 데 더 효과적이었다.
특히 어려운 샘플 구간에서 그 격차가 커져, 변분 상한이 난해한 상황에서도 올바른 중요도 식별에 도움을 줌을 보였다.
또한 각 layer의 관련 정보가 공정히 반영되고 있는지도 분석했는데, 이를 위해 IBA* 로 얻은 layer별 기여도와 CoIBA의 기여도를 공간적 유사도 측면에서 비교하였다.
중심축 커널 정렬(CKA) 방법으로 측정한 결과, CoIBA (Eq. (8))가 layer별 정보를 단순 합산한 경우(Eq. (4))보다 IBA*의 개별 layer 중요도와 높은 유사도를 보였다.
이는 CoIBA의 기여도 map이 각 layer의 정보를 골고루 반영하고 있음을 의미한다.
결국 변분 상한을 도입한 최적화는 설명 accuracy 향상과 layer간 기여 균형 두 측면에서 모두 유의미한 개선을 제공하였다.
Conclusion
이 논문에서는 Comprehensive Information Bottleneck for Universal Attribution (CoIBA)를 제안하여, ViT의 다층에 분산된 결정 근거를 모두 밝혀내는 새로운 설명 기법을 선보였다.
CoIBA는 여러 중간 layer에 정보 병목을 적용하면서 하나의 댐핑 비율을 공유함으로써, 기존 IBA가 놓쳤던 누락된 관련성까지 포착하는 통합적 기여도 map을 생성한다.
또한 변분적 상한 제약을 통해 layer별 정보량을 공정히 반영하도록 이론적으로 보장하였으며, 이를 통해 “각 layer에서 버려진 활성값은 결정에 정말 불필요한 것”임을 확신할 수 있게 만들었다.
다양한 ViT 계열 모델과 난이도 높은 데이터셋에 대한 실험에서 CoIBA는 기존의 propagation 기반, gradient 기반, IB 기반 등 여러 설명 방법들을 크게 앞서는 높은 설명 충실도를 보여주었다.
특히 CoIBA가 생성한 기여도 map은 모델의 예측에 실질적으로 영향력이 큰 입력 부분을 정확히 짚어낼 뿐 아니라, 타겟 클래스에 특화된 단서를 강조함으로써 사용자 입장에서 해석이 용이한 명확한 설명을 제공한다는 점을 확인하였다.
나아가 어려운 샘플에 대해서도 일관된 성능을 유지하여, 실제 응용 환경에서 신뢰할 수 있는 설명 방법임을 입증하였다.
Limitation
CoIBA는 기존 방식의 한계를 넘어 다층 종합 설명을 구현했지만, 여전히 몇 가지 제약과 한계가 존재한다.
- 계산 비용 측면에서 CoIBA는 IBA와 마찬가지로 각 입력마다 최적화 과정을 거쳐야 하므로, LRP처럼 한 번의 전향패스로 설명이 나오는 방법들보다 느리다.
- 다층에 Bottleneck을 적용하지만, 다행히 공유 파라미터로 최적화 변수를 줄여 IBA* 대비 효율은 개선했으나 근본적으로 추가 연산이 필요한 것은 피할 수 없다.
- noise 주입에 의존하는 방식이므로 설명 결과에 약간의 랜덤성이 개입할 수 있다.
- 이를 완화하기 위해 한 장의 이미지에 대해 여러 번 실행한 후 평균을 내는 등의 방법을 사용할 수도 있지만, 그만큼 시간이 더 든다.
- CoIBA는 분류 태스크의 시각적 기여도 map에 초점을 맞추고 있어, 이를 넘는 추론 과정 설명(예: 텍스트 설명이나 개념 단위 설명 등)에는 직접적인 기여를 하지 못한다.
- 또한 ViT 구조에 특화되어 제안되었지만, CNN 등의 다른 구조에 적용한 결과는 부록에 언급만 되어 있을 뿐 충분히 다루어지지 않았다.
- 다층 정보를 활용함에도 모델의 완벽한 투명성을 보장하는 것은 아니며, CoIBA가 제시하는 것은 여전히 포스트 hoc 기여도 map이기에 일반적인 한계 (기여도 map의 편향 등 )는 남아 있다.
이러한 부분들은 향후 연구에서 CoIBA를 더 빠르고 견고하게 개선하거나, 다른 구조 및 설명 형태로 확장하는 방향으로 보완될 수 있을 것이다.