[Paper Review] DDPM

Posted Jan 15, 2024 Updated Jun 11, 2024

By HahnGyuTak 18 min read

Denosing Diffusion Probability Model(DDPM) 논문 리뷰

Introduction

Diffusion 모델은 variational inference을 사용해 훈련된 Markov Chain이다. 일정 시간 뒤에 데이터와 일치하는 sample을 생성하기 위해 데이터에 노이즈를 점차적으로 추가하는 Markov Chain을 Reverse하는 과정을 학습한다. Gaussian Noise로 가정할 경우, Reverse process 역시 conditional Gaussian으로 설정할 수 있으며, Neural Network를 파라미터화 할 수 있다.

Background

Foward Process

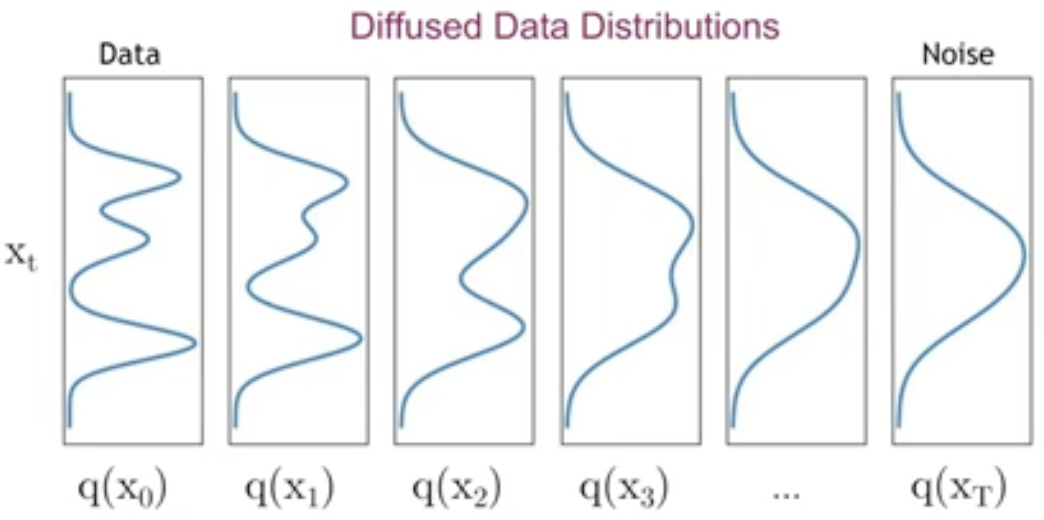
Diffusion모델이 다른 latent variable 모델과 구별되는 점은 foward process라 불리는 $q(x_{1:T}|x_0)$이다. 이 과정에서는 이미지를 Gaussian Noise를 점차 입혀서 $x_{0}$ 부터 $x_{t}$까지 만든다. $q(x_{1:T}|x_0)$ 는 Gaussian Noise를 variance schedule인 $\beta_1$ ~ $\beta_T$로 scaling하여여 점진적으로 추가하는 Markov chain으로 고정된다. $q(x_{1:T}|x_0) = \prod_{t=1}^{T}q(x_t|x_{t-1})$

$q(x_t|x_{t-1})$는 이전 time step인 $x_{t-1}$에 따라 Markov chain에 의해 결정될 $x_t$의 확률분포를 의미한다. Gaussian 분포로 가정하였기 때문에, $x_t$를 알기 위해서는 mean $\mu_t$와 std $\sigma_t$를 알아야 하며 $q(x_{t}|x_{t-1}) = N(x_{t}; \mu_t, \sigma_tI)$ 로 표현할 수 있다.

여기서, $x_t$의 mean과 std는 $x_{t-1}$로 다음과 같이 나타낼 수 있다.

$\mu_t = \sqrt{1-\beta_t}x_{t-1}$ , $\sigma_t = \beta_{t}$

즉 $q(x_t|x_{t-1})$는 다음과 같이 표현된다.

\[q(x_{t}|x_{t-1}) = N(x_{t}; \sqrt{1-\beta_{t}}x_{t-1}, \beta_{t}I)\]

여기서 noise를 $\sqrt{1-\beta_t}$로 scaling하는 이유는 variance가 발산하는 것을 방지하기 위해서이다.
파라미터화 하여 $\beta_t$를 학습할 수도 있지만 실험적으로 $\beta_t$를 상수로 고정하는 것이 성능이 좋다고 말한다. $\beta_t$는 0.0001에서 0.02까지 linear하게 증가하도록 설정하였다.

Reverse Process

Diffusion 모델은 denoising이 목적이다. $x_t$를 통해 $x_{t-1}$을 예측할 수 있다면, $x_0$또한 예측이 가능하다. Diffusion모델에서 reverse process는 결합확률분포인 $p_\theta(x_{0:T})$이다. 이는 $p(x_T) = N(x_T;0, I)$에서 시작하는 Gaussian으로 학습되는 Markov chain으로 정의된다. $p_\theta(x_{0:T}) := p(x_T)\prod_{t=1}^{T}p_\theta(x_{t-1}|x_t)$

여기서 $p_\theta(x_{t-1}|x_t)$는 $x_t$에 대한 $x_{t-1}$의 확률 분포를 의미하며 다음과 같이 구할 수 있다.

\[p_\theta(x_{t-1}|x_t):= N(x_{t-1};\mu_\theta(x_t, t), \Sigma_{\theta}(x_t, t))\] \[\left.\begin{matrix} p(x_T) = N(x_T; 0,I) \\ p(x_{t-1}|x_t) = N(x_{t-1}; \mu_{\theta}(x_t,t), \sigma_t^2I) \end{matrix}\right\} \;\; \mapsto \;\; p_{\theta}(x_{0:T}) = p(x_T)\prod_{t=1}^T{p_{\theta}(x_{t-1} | x_t})\]

학습은 Negative log likelihood를 minimize하는 방향으로 진행된다.

\[E_{q(x_0)}[- \log{p_\theta(x_0)} ]\leq E_{q}\left [-\log{\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}}\right ] = E_{q}\left [-log\;p(x_T) - \sum_{t\geq 1} \log{\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t}|x_{t-1})}}\right ] =:L \tag{3}\]

여기서 Negative log likelihood란 모델이 생성한 확률분포가 실제 데이터의 확률분포와 얼마나 일치하는지 측정하는 손실함수이다. variational bound는 KL Divergence를 활용하여 모델이 생성한 분포와 실제 데이터의 분포 간의 차이를 최소화하는 것에 기반한다.

Foward process에서 $\beta_t$는 하이퍼파라미터로 값을 유지하거나, reparameterization을 통해 학습할 수 있다. $\beta_t$가 작을 때, Foward($q$)와 Reverse($p$) Process는 같은 함수 형태를 띄기 때문에 Reverse Process($p$)의 표현은 부분적으로 $p_\theta (x_{t-1} | x_t)$의 Gaussian 조건부 선택에 의해 보장받는다.

reparameterization이란 주로 sampling 연산을 미분할 수 없어서 역전파를 사용하지 못하는 문제를 해결하기 위해 사용한다. sampling 과정을 바로 미분할 수 없으니, sampling 연산 과정의 파라미터를 바꿔서 미분이 가능하도록 변환하는 기법이다. ~~reparameterization에 대해 필자는 이 블로그를 통해 공부하였다. 참고가 되었음을 바라며 링크를 첨부한다. 링크~~

위 문단을 조금 더 풀어 설명하자면, $\beta_t$값이 작아질수록 두 process 과정은 비슷해진다. $p_\theta (x_{t-1} | x_t)$라는 조건부 확률은 파라미터 $\theta$에 의해 결정되며 Gaussian 분포를 따른다.

DDPM Loss function

Foward process는 다음과 같이 표현할 수 있다. $\alpha_t := 1-\beta_t$, $\overline{\alpha}_t := \prod_{t}^{s=1}\alpha_s$ 일때,

\[q(x_{t}|x_{0}) = N(x_{t}; \sqrt{\overline{\alpha}_{t}}x_{0}, (1-\overline{\alpha}_{t})I) \tag{4}\]

가우시안 nosie를 순차적으로 적용하기 때문에 원하는 타임 step으로 바로 이동할 수도 있지 않을까? → DDPM

$t$번의 sampling을 통해 step을 하나하나 거치며 noise를 추가하여 $x_t$를 만들수 있지만 DDPM은 한번에 $x_t$를 얻는다.

sampling을 통해 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{(1-\bar{\alpha}_t)}\epsilon$ 이라는 식을 얻을 수 있다. 즉 원하는 step으로 바로 건너뛰어 $x_t$를 얻을 수 있다는 것이다.

stochastic gradient descent(확률적 경사하강법)을 이용해 최적화하면 효율적인 학습이 가능하다.

$L$ Eq 3.에서 ELBO(Evidence of Lower Bound)로 우항을 정리하고 풀면 다음과 같이 쓸 수 있다. (Eq. 5)

\[L = E_q \left [ \underbrace{D_{KL}(q(x_T|x_0) || p(x_T)}_{L_T} + \sum_{t > 1}\underbrace{D_{KL}(q(x_{t-1}|x_t, x_0)||p_\theta(x_{t-1}|x_t))}_{L_{t-1}} \underbrace{- \log{p_\theta(x_0|x_1)}}_{L_0} \right] \tag {5}\]

수식 (5)는 추후 자주 언급되니 기억해놓도록 하자.

수식(5)에서 사용한 KL divergence는 Gaussian 간의 비교이다. 그러므로 몬테-카를로 추정 대신, 닫힌 수식 형태를 이용한 라오-블랙웰 정리를 이용해 계산할 수 있다.

닫힌 형식이란, 다른 수학적 표현이나 무한 합이나 적분 없이 특정한 형태로 명확하게 나타낼 수 있거나 특정 값이 직접 계산되어 나오는 형태을 말한다.

몬테 카를로 추정 (Monte-carlo estimation)
Random Sampling을 반복하여 함수의 값을 수리적으로 근사하는 알고리즘이다. 계산하려는 값이 닫힌 형식으로 표현되지 않거나 복잡한 경우에 근사적으로 계산하기 위해 사용된다.

라오-블랙웰 정리 (Rao Blackwell Theorem)
어떤 추정량이 있을 때, 충분 통계량에 대한 조건부 기댓값을 취함으로써 더 좋은 추정량을 만들 수 있음을 뜻한다.
$S(X)$ : 추정량, $T(X)$ : 충분통계량, $S^*(X) = \mathbb{E}\left [S(X) | T(X) \right ]$라고 할때, 다음이 성립한다.
\[\mathbb{E}\left [S^*(X) \right ] = \mathbb{E}\left [S(X) \right ]\\ Var\left [S^*(X) \right ] \leq Var\left [S(X) \right ]\]

$L_T$의 경우 $ p(x_T)$는 가우시안으로 가정하고, $q$ 역시 $x_T$는 가우시안 노이즈이기 때문에 두 분포는 거의 일치한다. 즉 $L_T$는 항상 0에 가까운 상수이다.

$L_{t-1}$의 경우, KL Divergence의 $q(x_{t-1}|x_t, x_0)$와 $p_\theta(x_{t-1}|x_t)$는 Normal distributions이다.

\[q(x_{t-1}|x_t, x_0) = N(x_{t-1}; \widetilde{\mu}_t(x_t, x_0), \widetilde{\beta}_tI) \tag{6}\]

이때 $\widetilde{\mu}_t(x_t, x_0)$는 다음과 같다.

\[\widetilde{\mu}_t(x_t, x_0) := \frac{\sqrt{\overline{\alpha}_{t-1}}\beta_t}{1 - \overline{\alpha}_t}x_0 + \frac{\sqrt{\alpha_t}(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}x_t, \;\;\;\;\; \widetilde{\beta}_t := \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\beta_t \tag{7}\]

Diffusion models and Denoising Autoencoders

여기는 위 Eq 5.의 loss식에 부분부분을 살펴보는 부분이다.

1. Foward process and $L_T$

논문에서는 Train이 진행 중일때 foward process의 $\beta _t$를 무시하고 상수로 고정하였다. 원래 $\beta _t$는 reprarameterization으로 학습 가능한 값이었지만, 그대신 상수로 고정(0.0001 ~ 0.02)하고 무시한다. 즉 learnable한 파라미터가 없다.

2. Reverse process and $L_{1:T-1}$

첫번째로, $p_\theta(x_{t-1}|x_t):= N(x_{t-1};\mu_\theta(x_t, t), \Sigma_{\theta}(x_t, t))$에서 $ \Sigma_{\theta}(x_t, t)) = \sigma ^2I$를 Train이 진행되지않을때의 종속변수로 정의한다. 실험적으로, $\sigma _{t} ^2 = \beta _t$와 $\sigma _{t} ^2 = \widetilde{ \beta} _t = \frac{1- \overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\beta_t$는 비슷한 결과를 보인다.

$\sigma _{t} ^2 = \beta _t$는 $x_0 \sim N(0, I)$에서 최적이며, $\sigma _{t} ^2 = \widetilde{ \beta} _t = \frac{1- \overline{\alpha}_{t-1}}{1-\overline{\alpha}_t}\beta_t$는 한 점 $x_0$에서 최적이다.

두번째로, 평균인 $\mu_\theta(x_t, t)$를 나타내기위해 우리는 $L_t$ 분석에 기반한 특정 파라미터화 방법을 제안한다. $p_\theta(x_{t-1}|x_t):= N(x_{t-1};\mu_\theta(x_t, t), \sigma _t ^2 I)$에서 우리는 다음과 같이 쓸 수 있다.

\[L_{t-1} = \mathbb{E}_q \left [\frac{1}{2\sigma_t^2} \left || \widetilde{\mu}_t(x_t, x_0) - \mu_\theta(x_t, t)\right ||^2 \right] + C \tag{8}\]

$C$는 $\theta$와 상관없는 변수이다. 위 식에서 $\mu_\theta$의 가장 간단한 parameterization은 $\widetilde{\mu}_t$를 예측하는 모델임을 알 수 있다. 여기서 $\widetilde{\mu}_t$는 foward process의 사후 확률 평균이다.

식 (4)를 $x_t(x_0, \epsilon) = \sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon \;… \; (\epsilon \sim N(0, I))$로 reparameterizing하고 식 (7)을 적용하여 식 (8)을 확장할 수 있다.

\[\begin{align} L_{t-1} - C &= \mathbb{E}_{x_0, \epsilon} \left [\frac{1}{2\sigma_t^2} \left |\left | \widetilde{\mu}_t\left ( x_t(x_0, \epsilon), \frac{1}{\sqrt{\overline{\alpha}_t}}(x_t(x_0, \epsilon) - \sqrt{1-\overline{\alpha}_t}\epsilon) \right ) -\mu_\theta(x_t(x_0, \epsilon), t) \right|\right|^2 \right ] \tag{9} \nonumber \\ &=\mathbb{E}_{x_0, \epsilon} \left [\frac{1}{2\sigma_t^2} \left |\left | \frac{1}{\sqrt{\alpha_t}} \left ( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon \right) - \mu_\theta(x_t(x_0, \epsilon), t) \right | \right |^2 \right ] \tag{10} \end{align}\]

식(10)은 $\mu_\theta$가 주어진 $x_t$로 $\frac{1}{\sqrt{\alpha_t}} \left ( x_t- \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon \right)$를 예측해야함을 나타낸다. $x_t$는 모델의 Input으로 사용가능하다.

Eq 10. 유도과정
Eq 8.에서 Eq 9.가 되는 과정은 $x_t(x_0, \epsilon) = \sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon$를 $x_0$에 따른 식으로 변환하여 대입하고 C를 이항한 것이다.
\[x_0 = \frac{x_t - \sqrt{1-\overline{\alpha}_t}\epsilon}{\sqrt{\overline{\alpha}_t}} = \frac{x_t - \sqrt{1-\overline{\alpha}_t}\epsilon}{\sqrt{\alpha} \sqrt{\overline{\alpha}_{t-1}}}\]
Eq 8.에서 Eq 10.으로의 유도 과정은 결국 $\widetilde{\mu}_t(x_t, x_0)$를 $\frac{1}{\sqrt{\alpha_t}} \left ( x_t(x_0, \epsilon) - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon \right)$으로 바꾸는 과정이다.
Eq 7.에 앞에서 구한 $x_0$ 식을 대입한다.
\[\begin{align} \widetilde{\mu}_t(x_t, x_0) &= \frac{\sqrt{\overline{\alpha}_{t-1}}\beta_t}{1 - \overline{\alpha}_t}x_0 + \frac{\sqrt{\alpha_t}(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}x_t, \nonumber \\ &= \frac{\sqrt{\overline{\alpha}_{t-1}}\beta_t}{1 - \overline{\alpha}_t} * \frac{x_t - \sqrt{1-\overline{\alpha}_t}\epsilon}{\sqrt{\alpha} \sqrt{\overline{\alpha}_{t-1}}} + \frac{\sqrt{\alpha_t}(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}x_t, \nonumber\\ &= x_t \left( \frac{\beta_t}{\sqrt{\alpha_t}(1 - \overline{\alpha}_t)} + \frac{\alpha_t(1 - \overline{\alpha}_{t-1})}{\sqrt{\alpha_t}(1 - \overline{\alpha}_t)}\right) - \frac{\beta_t \sqrt{1-\overline{\alpha}_t}}{\sqrt{\alpha_t}(1 -\overline{\alpha}_t)}\epsilon \nonumber\\ &= \frac{1}{\sqrt{\alpha_t}}\left \{x_t\left( \frac{\beta_t + \alpha_t - \overline{\alpha}_t}{1 - \overline{\alpha}_t} \right) - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}} \epsilon \right \} \nonumber \end{align}\]
마지막에서 $\beta_t = 1 - \alpha_t$이므로 Eq 10.이 유도된다.

\[\mu_\theta(x_t, t) = \widetilde{\mu}_t \left( x_t, \frac{1}{\sqrt{\overline{\alpha}_t}}(x_t - \sqrt{1 - \overline{\alpha}_t}\epsilon_\theta x_t) \right) = \frac{1}{\sqrt{\alpha_t}} \left ( x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta(x_t, t) \right) \tag{11}\]

$\epsilon_\theta$는 $x_t$로 $\epsilon$을 예측하기 위한 함수 근사치이다. $x_{t-1} \sim p_\theta(x_{t-1} | x_t)$를 sampling하는 것은 $z \sim N(0, I)$일 때 $x_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left ( x_t- \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta(x_t, t) \right)$를 계산하는 것을 의미한다.

식(11)로 parameterization하였을때, 식(10)은 다음과 같이 간단히 된다.

\[\mathbb{E}_{x_0, \epsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\overline{\alpha}_t)} \left|\left| \epsilon - \epsilon_\theta(\sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon, t) \right|\right|^2 \right] \tag{12}\]

유도과정
\[\begin{align} L_{t-1} - C &=\mathbb{E}_{x_0, \epsilon} \left [\frac{1}{2\sigma_t^2} \left |\left | \frac{1}{\sqrt{\alpha_t}} \left ( x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon \right) - \mu_\theta(x_t, t) \right | \right |^2 \right ] \nonumber \\ &= \mathbb{E}_{x_0, \epsilon} \left [\frac{1}{2\sigma_t^2} \left |\left | \frac{1}{\sqrt{\alpha_t}} \left ( x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon \right) - \frac{1}{\sqrt{\alpha_t}} \left ( x_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta(x_t, t) \right) \right | \right |^2 \right ]\nonumber\\ &= \mathbb{E}_{x_0, \epsilon} \left [\frac{1}{2\sigma_t^2} \left |\left | \frac{1}{\sqrt{\alpha_t}} \frac{\beta_t}{\sqrt{1-\overline{\alpha}_t}}\left ( \epsilon -\epsilon_\theta(x_t, t) \right) \right | \right |^2 \right ]\nonumber \\ &= \mathbb{E}_{x_0, \epsilon} \left [\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\overline{\alpha}_t)} \left |\left |\left ( \epsilon -\epsilon_\theta(x_t, t) \right) \right | \right |^2 \right ]\nonumber \\ \end{align}\]
여기서 앞에서 식 (4)를 $x_t(x_0, \epsilon) = \sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon \;… \; (\epsilon \sim N(0, I))$로 reparameterizing하였고, 이를 대입하면 식 (12)가 나온다.

요약하면, reverse process의 평균 함수 근사치인 $\mu_\theta$를 학습하여 $\widetilde{\mu}_t$를 예측하거나, parameterization을 수정하여 $\epsilon$을 예측하도록 학습할 수 있다는 것이다. $\epsilon$ predict parameterization은 Langevin dynamics과 유사하며, Denoising Score matching 목적이 비슷한 Diffusion 모델의 Variational Bound를 단순화한다.

3. Data scaling, Reverse process decoder, and $L_0$

Discrete log likelihood를 얻기 위해, Reverse process의 마지막 부분을 Gaussian $N(x_0; \mu_\theta (x_1, 1), \sigma_1^2 I)$에서 파생된 Independent discrete Decoder로 설정한다.

\[\begin{align} p_\theta(x_0|x_1) &= \prod_{i=1}^{D} \int_{\delta_-(x_0^i)}^{\delta_+(x_0^i)} N(x;\mu_\theta^i(x_1,1),\sigma_1^2)dx \nonumber\\ \delta_+(x) &= \begin{cases} \infty & \text{ if } x=1 \\ x+\frac{1}{255} & \text{ if } x<1 \end{cases} \;\;\;\;\;\; \delta_-(x) = \begin{cases} -\infty & \text{ if } x=-1 \\ x-\frac{1}{255} & \text{ if } x>-1 \end{cases} \tag{13} \end{align}\]

여기서 $D$는 데이터 차원 수이다.

4. Simplified training objective

Algorithm 1 Training (noise를 더해가는 과정)

step $t$에서 noise가 얼마나 추가되었는지를 학습하고 예측한다.

repeat
    $x_0 \; \sim \; q(x_0)$
    $t \; \sim \; Uniform({ 1, …, T})$
    $\epsilon \; \sim \; N(0, I)$
    Take gradient descent step on
\[\bigtriangledown _\theta \left |\left | \epsilon - \epsilon_\theta \left (\sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon, t\right) \right|\right|^2\]
until converged

Algorithm 2 Sampling (Train 후, Gaussian noise에서 순차적으로 denoising하는 과정)

Makorv chain으로 parameterization 됨

$x_T \; \sim \; N(0, I)$
for $t = T, \cdots , 1$ do
$z \sim N(0, I)$ if $ t > 1$, else $z = 0$
$x_{t-1} = \frac{1}{\sqrt{\alpha_t}}\left (x_t - \frac{1 - \alpha_t}{\sqrt{1-\overline{\alpha}_t}}\epsilon_\theta (x_t, t) \right) + \sigma_t z$
end for
return $x_0$

Sampling 과정인 Algorithm 2는 데이터 밀도의 학습된 기울기인 $\epsilon_\theta$를 사용한 Langevin 역학과 유사하다._
Langevin dynamics (랑주뱅 역학)
물리학에서 분자 시스템의 움직임을 수학적으로 모델링한 것이다. 확률적 미분 방정식을 사용해 자유도를 생략하면서 단순화된 모델을 사용하는 것이 특징이다.

위 Loss term에서 중요한 부분은 Variational bound인 $L_{t-1}$ $L_0$이다. 논문에서는 Loss term을 다음과 같이 단순화시켰다.

\[L_{simple}(\theta) = \mathbb{E}_{t, x_0, \epsilon}\left[\left|\left| \epsilon - \epsilon_\theta(\sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\epsilon, t)\right|\right|^2 \right] \tag{14}\]

$t$는 1에서 $T$사이의 값이며, $t=1$인 경우에는 $L_0$에 해당하며, $\sigma_1^2$를 무시하고 근사화된 Eq 13.의 적분이다. $t > 1$인 경우에는 Eq 12.에서 가중치가 없는 버전에 해당한다. 이는 NCSN Denoting score matching 모델에서 사용하는 loss 가중치와 유사하다. Foward process에서 분산 $\beta_t$는 고정되어있어 $L_T$는 나타내지 않는다. 위 Algorithm 1은 단순화된 Object function을 가진 전체 Train 과정을 표시한다.

위 식은 ㄴ$t$ 작을 때 loss term의 중요도를 낮춘다. 이 term은 매우 적은 양의 noise가 있는 데이터를 denoising하도록 train하므로, $t$가 큰 경우에서 어려운 denoising 과정에 집중할 수 있도록 하기 위함이다.

Experiments

$T$는 1000으로, backbone 모델은 U-net을 사용하였다.

Paper Review, Computer Vision, Generative model

AI generative Diffusion

This post is licensed under CC BY 4.0 by the author.