[Paper Review] Escaping Plato's Cave: Towards the Alignment of 3D and Text Latent Spaces

[논문 리뷰] Escaping Plato’s Cave: Towards the Alignment of 3D and Text Latent Spaces

Escaping Plato’s Cave: Towards the Alignment of 3D and Text Latent Spaces

Souhail Hadgi, Luca Moschella, Andrea Santilli, Diego Gomez, Qixing Huang, Emanuele Rodolà, Simone Melzi, Maks Ovsjanikov

CVPR 2025

arXiv

다양한 Text, 3D Encoder들의 alignment 여부를 분석하고, 향상된 Alignment method를 제안한 논문.

Introduction

CLIP은 Text-Image 간의 alignment를 목적으로 학습되었지만, 최근 연구에서는 unimodal Text Encoder와 Vision Encoder의 latent space 구조는 유사한 proximity 구조를 갖고 있으며, 소수의 pair만으로도 정렬이 가능하다는 것이 관찰된다. 이러한 결과는 다양한 모달리티가 실제 세계의 공통된 구조를 반영하는 latent representation으로 수렴하게 된다는 해석으로 이어지며, 이를 플라톤 표현 가설(Platonic Representation Hypothesis)이라고 부른다. 이 가설은 각기 다른 표현들이 현실의 projection이라는 관점에서 이해된다.

하지만, 실제 세계는 3차원이기 때문에, 2D Vision 또는 Text Encoder에서 학습된 구조가 3D Encoder에서의 특징과 어떻게 연결되는지에 대한 질문이 제기된다. 이 문제에는 다음과 같은 어려움이 존재한다:

1. 대규모 3D 데이터셋은 최근에야 등장
2. 기존 대부분의 3D 파운데이션 모델은 2D 또는 Text Encoder을 고정시킨 채로 훈련되며, 이는 post-training alignment의 가능성을 제한
3. 3D 데이터에 대한 보편적인 아키텍처와 Train objective가 정립되어 있지 않으며, 자주 사용되는 구조들은 일반화 성능이 낮다.

이 논문은 이러한 맥락 속에서 3D와 Text representation 간의 관계를 처음으로 본격적으로 분석한다. 다양한 3D 및 Text Encoder 간의 post-training alignment 방법을 공식화하고, 그 정확성과 효용성을 실험적으로 비교 분석한다.

논문에서 밝힌 주된 관찰은 다음과 같다.

1. Vision-Text unimodal latent space alignment 분석을 3D unimodal Encoder와 Text로 확장하여 이러한 Latent space 간의 제한된 유사성과 현재 alignment 접근 방식의 낮은 효율성을 조명
2. Canonical Correlation Analysis (CCA)와 기존 align 기법들(예: Affine 변환, Local CKA)을 결합하여 Text-3D의 cross-modal alignment을 위한 효율적인 접근 방식을 제안
3. Feature space와 그의 subspace간의 관계를 분석하여 geometric(기하학적) & semantic(의미적) representation을 구분

---

Method

1. Preliminaries

Centered Kernel Alignment (CKA)

CKA는 최근의 여러 연구에서 널리 사용되는 신경망 feature representation 간 유사성을 비교하는 측정 지표다.

• 두 특징 행렬 $X \in \mathbb{R}^{n \times p}$, $Y \in \mathbb{R}^{n \times q}$가 주어진다.

• 각각에 대해 커널 함수 $k, l$을 적용하여 커널 행렬을 만든다:

  $K = k(X, X) \in \mathbb{R}^{n \times n}, \quad L = l(Y, Y) \in \mathbb{R}^{n \times n}$

CKA는 다음과 같이 정의된다:

\[\text{CKA}(K, L) = \frac{\text{HSIC}(K, L)}{\sqrt{\text{HSIC}(K, K) \cdot \text{HSIC}(L, L)}}\]

여기서 HSIC (Hilbert-Schmidt Independence Criterion)는 다음과 같이 계산된다:

\[\text{HSIC}(K, L) = \frac{1}{(n-1)^2} \cdot \text{tr}(KHLH)\]

• $H = I - \frac{1}{n}11^\top$ 는 centering matrix이다.

이 식은 입력 데이터를 평균 0으로 중심화한 후의 커널 간의 상호의존성을 나타낸다.

Canonical Correlation Analysis (CCA)

CCA는 두 데이터셋 간에서 선형 변환을 찾아, 투영된 결과들 사이의 상관관계를 최대화하는 통계적 방법이다.

• 두 데이터셋 $X \in \mathbb{R}^{n \times d_1}, Y \in \mathbb{R}^{n \times d_2}$가 있다고 하자. (각각 평균 0으로 정규화됨)
• CCA는 두 개의 projection matrix $W_X \in \mathbb{R}^{d_1 \times k}$, $W_Y \in \mathbb{R}^{d_2 \times k}$를 찾아낸다.
• 각각의 데이터를 k-차원 공간으로 projection한 결과 $XW_X, YW_Y$가 서로 가장 높은 상관관계를 갖도록 한다.

이 문제는 다음과 같이 최적화된다:

\[\max_{W_X, W_Y} \ \text{corr}(XW_X, YW_Y)\]

• 여기서 $\text{corr}(\cdot, \cdot)$는 두 투영된 변수 간의 상관계수를 의미한다.

이 과정을 통해 서로 다른 representation space 사이의 공통된 latent representation 방향을 찾아낼 수 있다.

“3D 공간에서 의미 있는 방향 하나”와 “텍스트 공간에서 의미 있는 방향 하나”를 찾아서, 이 둘의 상관관계가 가장 크도록 projection 해주는 방법

⟶ 결국, 모든 정보가 아닌, 진짜 의미 있는 축들만 추출해서 정렬 성능을 극대화

---

2. Alignment approaches

논문에서는 Affine 변환과 CKA 기반 alignment 방식을 함께 검토하며, 이들이 3D-Text latent space alignment에 있어 갖는 한계를 분석하고 이를 보완할 수 있는 방법을 제안한다.

Latent Space Translation via Affine Transformation

latent space $\mathcal{X}$를 다른 space $\mathcal{Y}$에 매핑하는 affine 변환 $T (\mathbf{x}) = R\mathbf{x} + b, \;\; \forall\mathbf{x} \in \mathcal{X}$를 추정할 수 있다. 이때 $R$은 affine 변환 matrix, $b$는 bias vector이다.

두 latent space의 ground-truth 쌍(anchor)을 통해 $T$를 학습하며, $b$가 0인 경우 MSE loss를 통해 $R$를 구할 수 있다.

Local CKA-based retrieval and matching

두 feature 집합 사이에서 유사도를 측정하는 CKA는 ground-truth가 잘 정렬되었을 때 최대가 된다. 즉 unseen 데이터를 anchor 세트에 포함시켜, matching을 수행할 수 있다. 정렬된 feature 집합 $X_A$, $Y_A$가 있을 때 query pair $(\mathbf{x}_q, \mathbf{y}_q)$에 대한 local CKA는 다음과 같다.

\[\text{localCKA}(\mathbf{x}_q, \mathbf{y}_q) = \text{CKA}(K_{[X_A, \mathbf{x}_q]}, K_{[Y_A, \mathbf{y}_q]})\]

• 여기서 $[X, \mathbf{x}]$는 행렬 $X$에 벡터 $\mathbf{x}$를 열 방향으로 붙인 것을 의미한다.

query 쌍들에 대해 모든 가능한 조합을 입력하여 CKA를 계산하면, anchor 쌍은 가장 높은 local CKA 점수를 가지게 된다.

---

3. Proposed method

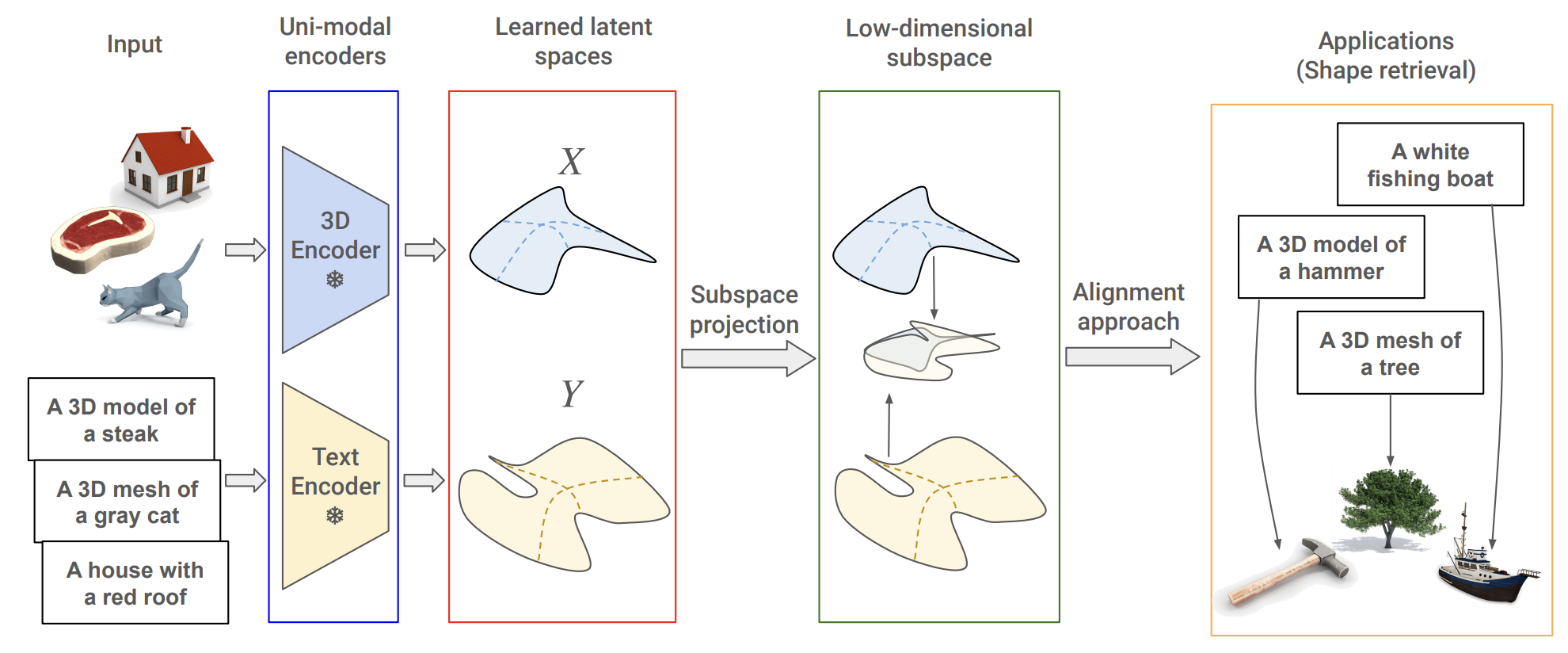
목표는 pretrain된 3D & Text Encoder의 latent space를 align하는 것이다.

$n$개의 (caption, point cloud) pair가 주어졌을 때, 이를 각각 임베딩하여 $X \in \mathbb{R}^{n\times p}$, $Y \in \mathbb{R}^{n\times q}$로 만든다. 여기서 anchor pair를 선택한다. ( $X_A \in \mathbb{R}^{n_A \times p}$, $Y_A \in \mathbb{R}^{n_A \times q}$)

Common Subspace Projection

본 논문에서는 3D(point cloud)와 Text의 전체 latent space를 직접 align하는 것보다, 서로 잘 정렬되는 저차원 subspace에서 정렬하는 것이 효과적이라고 밝힌다.

이를 위해 anchor 쌍 $X_A, Y_A$에 대해 CCA를 적용하여, 서로 대응되는 공통된 k-차원 subspace를 찾는다.

이때 $k < p, q$이며, $W_X \in \mathbb{R}^{p \times k}, W_Y \in \mathbb{R}^{q \times k}$는 각각의 projection 행렬이며 모든 sample을 projection하여 차원을 축소시킨다.

\[X^r = X W_{X_A}, \quad Y^r = Y W_{Y_A}\]

특히 anchor 쌍은 $X_A^r, Y_A^r \in \mathbb{R}^{n_A \times k}$로 표현된다. 이렇게 projection을 통해 여러 모달리티 간에 상관관계가 높은 feature를 분리하여 align을 개선한다.

Alignment of Projected Latent Spaces

projection되어 축소된 latent space에서 앞서 설명한 align 방식인 affine 또는 local CKA를 적용한다.

• Affine 변환

  • projection된 anchor 쌍 $X_A^r, Y_A^r$ 를 사용하여 파라미터 $R$과 $b$를 optimization한다. \(T(X^r) = RX^r + b\)

• local CKA

  • query 쌍 $(\mathbf{x}^r_q, \mathbf{y}^r_q)$에 대해, anchor 쌍을 사용하여 CKA를 계산한다. \(\text{localCKA}(\mathbf{x}_q^r, \mathbf{y}_q^r) = \text{CKA}(K_{[X_A^r, \mathbf{x}_q^r]}, K_{[Y_A^r, \mathbf{y}_q^r]})\)

Experimental setup

1. Pre-training Dataset

ShapeNet

기존의 3D point cloud 기반 연구들은 주로 ShapeNet을 기반으로 이루어져 왔다.

• ShapeNet은 총 51,300개의 주석이 달린 3D 객체들로 구성되며, 55개 category를 포함한다.
• category가 제한적이라는 단점이 존재한다.

Objaverse

• Objaverse는 80만 개 이상의 다양한 실제 기반 3D 객체를 포함하고 있어, unimodal 및 multimodal 학습 모두에 적합하다.
• Objaverse를 기반으로 순수 단일모달(unimodal) 방식으로 사전학습을 수행한 연구는 아직 부족한 상황이다.

2. Encoders

본 논문은 다양한 3D 인코더와 텍스트 인코더 조합을 실험하여 모델 복잡도에 따른 align 성능 차이를 분석한다.

Multi-modal 3D Encoder

Objaverse의 3D-이미지-텍스트 triplet으로 pretrained OpenShape 모델을 사용한다. contrastive loss로 학습되며 3D Encoder를 CLIP Encoder와 align한다.

OpenShape의 파이프라인에는 이미지에 Blip을 적용하여 생성된 caption과 이를 GPT-4로 개선한다.

다양한 architecture를 평가하기 위해 2가지 3D Encoder를 포함한다.

• PointBERT (Transformer 기반 3D 인코더)
• MinkowskiNet (SparseConv) (sparse convolution 기반 인코더)

Uni-modal 3D Encoder

masked point reconstruction과 unimodal contrastive loss를 사용하여 Objaverse 데이터셋으로 PointBERT를 pretrain한다.

추가로 pretrain된 두 모델인 MinkowskiNet과 더 단순한 PointNet을 실험한다.

이들은 모두 입력 형태 변형에 기반한 shape-level contrastive 학습으로 사전학습되며, 모든 3D Encoder의 latent space 차원은 512로 고정된다.

Text Encoder

OpenShape에서 사용된 것과 동일한 OpenCLIP의 ViT-bigG-14 텍스트 인코더를 사용한다.

unimodal 텍스트 인코더로는 다음을 추가로 실험한다:

• BERT**

• RoBERTa

이를 통해 Multi-modal vs Uni-modal이 align 성능에 미치는 영향을 분석한다.

3. Downstream task

평가에는 Objaverse-LVIS라는 test subset을 사용한다.

• 총 1,156개의 실제 객체 category로 구성되며, 사람이 검증한 데이터셋이다.
• 이 데이터는 사전학습 단계에서는 사용되지 않는다.
• Cap3D를 사용해 각 3D 객체에 대해 향상된 캡션이 생성된다.

수행되는 주요 과제는 두 가지이다:

1. Matching Task

   • 텍스트 캡션과 3D 객체 간의 매칭 정확도를 평가한다.

   • linear sum assignment을 사용하여 쌍을 완성한다.

     linear sum assignment은 최적 할당 문제를 해결하는 알고리즘이다.

     특히, n개의 항목을 n개의 항목에 일대일로 대응시키는 과정에서, 전체 cost의 합이 최소가 되도록 매칭을 찾는다.

     논문에서는 n개의 3D 객체 쿼리와 텍스트 캡션 쿼리로 각 쌍마다 유사도(또는 거리, loss)를 계산하여 cost matrix을 만든다

2. Retrieval Task

   • 주어진 텍스트 쿼리에 대해 정확한 3D 객체를 찾아야 한다.
   • 텍스트 → 3D 또는 3D → 텍스트 검색이 가능하다.

이 두 과제는 기존 Vision-Language 연구들에서도 cross modal 성능 평가 기준으로 널리 사용되어 왔다.

Result

1. Are 3D and Text Latent Space similar ?

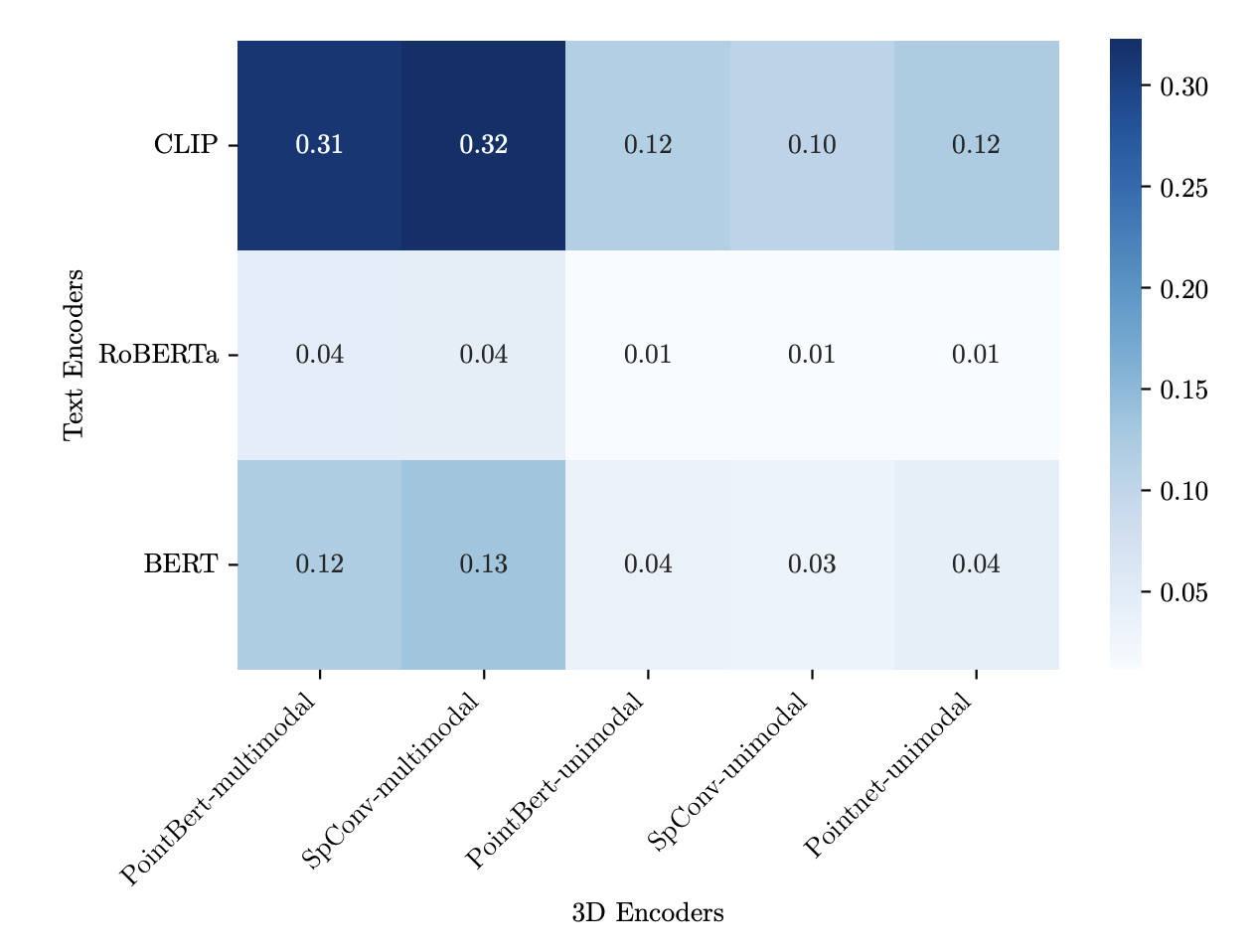
align 되지않은 3D-Text feature space 간의 유사성을 평가하기 위해 unimodal 및 multimodal Encoder에 대해 linear CKA 점수를 계산한다.

기존 연구에 따르면, Vision-Text 인코더(CLP 등)는 CKA 유사도가 30~48% 정도로 높다.

반면, 3D-Text 쌍에서는 CKA 최대값이 0.12에 불과하다.

PointBERT (unimodal) – CLIP 조합 → 0.12

이는 3D Encoder는 텍스트 Encoder와 구조적으로 상당히 다르다는 점을 보여준다.

• 멀티모달 훈련이 없을 경우, 3D 인코더는 텍스트와 의미적으로 거의 정렬되지 않는다.
• CLIP과 같이 멀티모달로 훈련된 인코더와는 정렬도가 높다.

또한 3D Encoder와 Text Encoder를 align할 때,

• 3D Encoder - CLIP Text Ecoder
  • PointBERT-CLIP : 0.12
• 3D Encoder - unimodal Text Encoder
  • PointBERT-RoBERTa : 0.04

위 결과를 보면 pretrain 중 align이 없음에도 불구하고 CLIP Text Encoder에 내장된 시각적 이해가 Image-Text 영역을 넘어 3D representation을 포함하도록 확장된다는 것을 시사한다.

2. Latent Space Alignment results

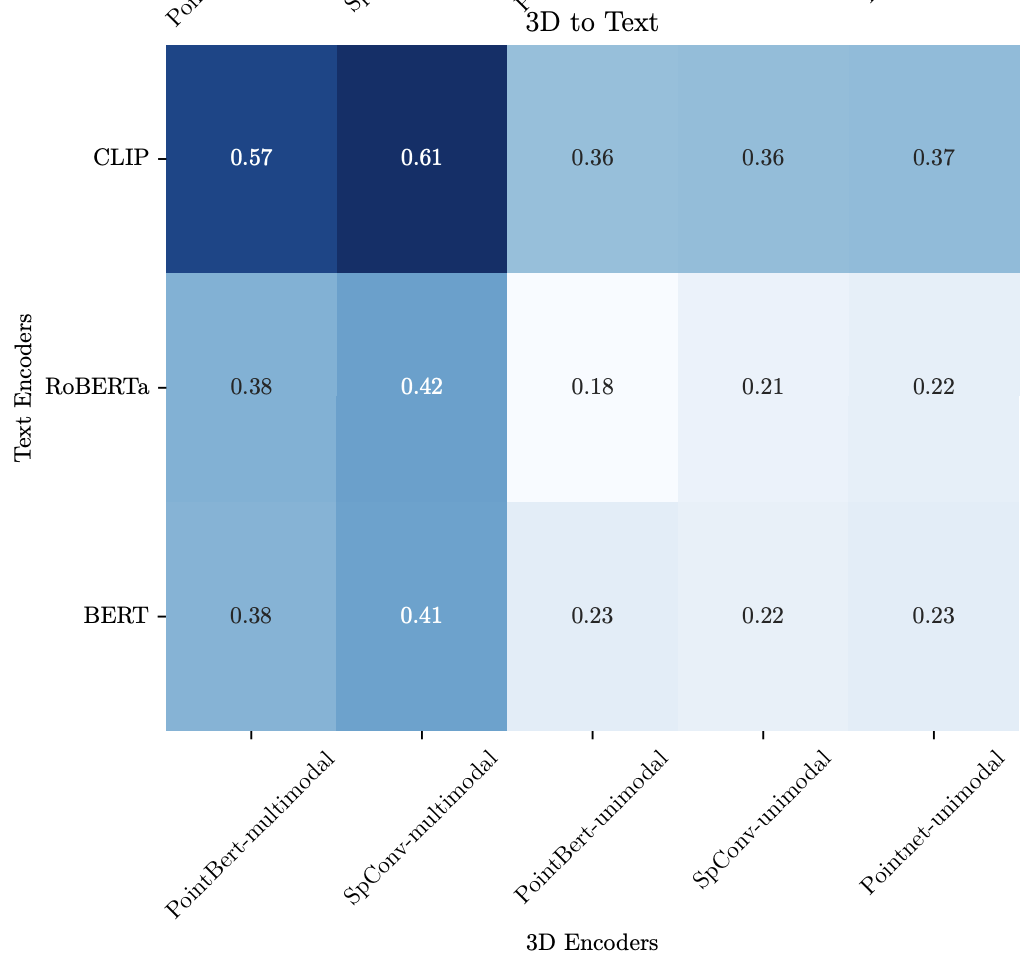
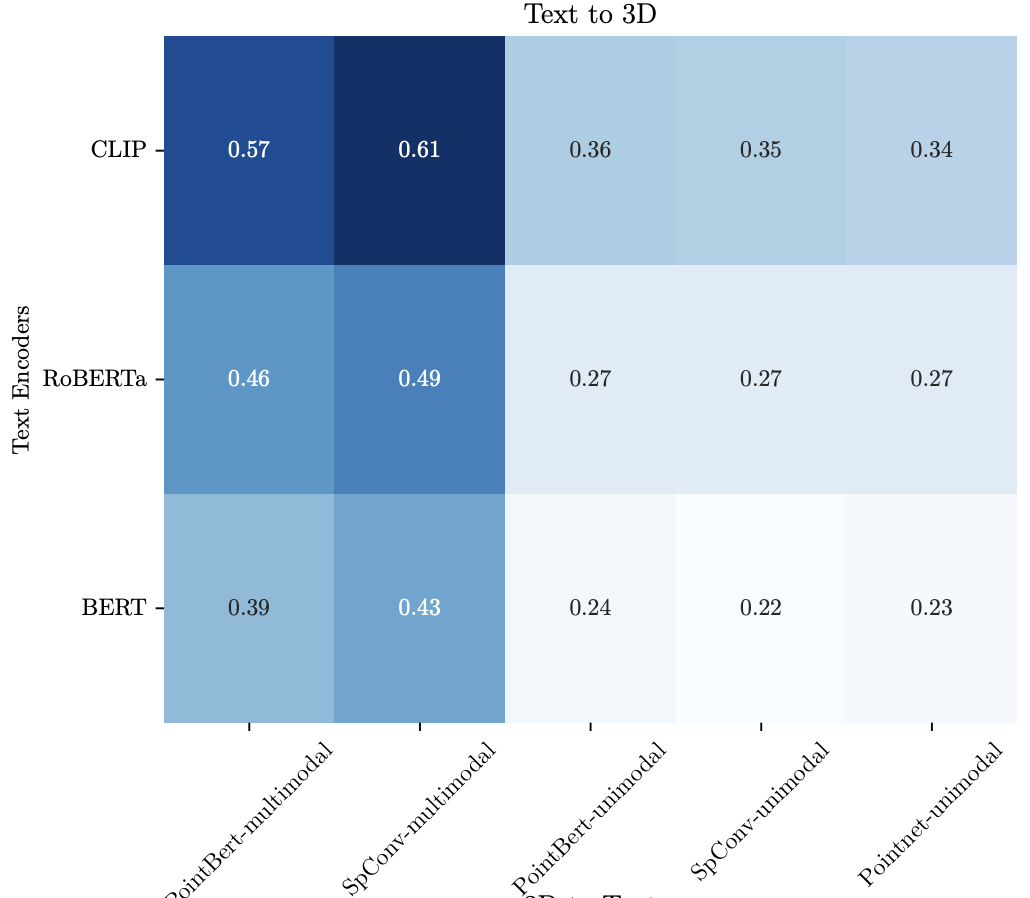
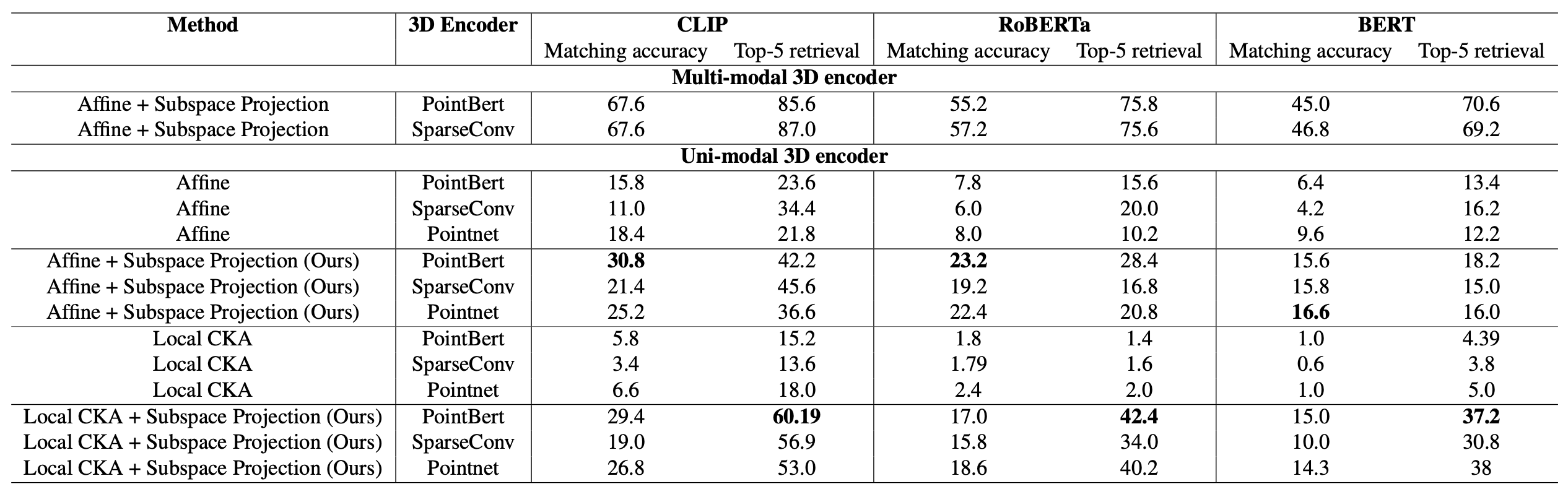
Matching & Retrieval task을 사용하여 앞에서 설명한 alignment 접근법의 성능을 평가하고 3D 및 Text Encoder alignment에 대해 분석한다.

subpace 차원을 $d = 50$으로 고정하고 anchor 수를 30, 000으로 설정한다. downstream task의 경우, 500개의 query를 sampling하고 3가지 seed로 실험한다.

Affine 변환 결과는 Text → 3D 정렬 방향 기준으로 보고하지만, 3D → Text 방향도 유사한 성능을 보인다 (아래 그림 참고).

Existing Approaches Enable Limited Alignment

먼저, 기존 문헌에서 효과를 보였던 Affine 변환 방식과 Local CKA 방식을 3D-텍스트 align에 적용해본다.

위 표에서 볼 수 있듯이, 이들 방식은 정렬 이전 baseline 대비 약간의 성능 향상만을 보여준다.

unimodal 3D Encoder는 Matching 및 Retrieval task 성능이 거의 0에 수렴하며, 정렬 이후에도 소폭 개선되는 수준이다.

이 결과는 unimodal 3D 인코더는 Vision-Text Alignment 성능에 도달하기엔 매우 제한적이라는 것을 보여준다.

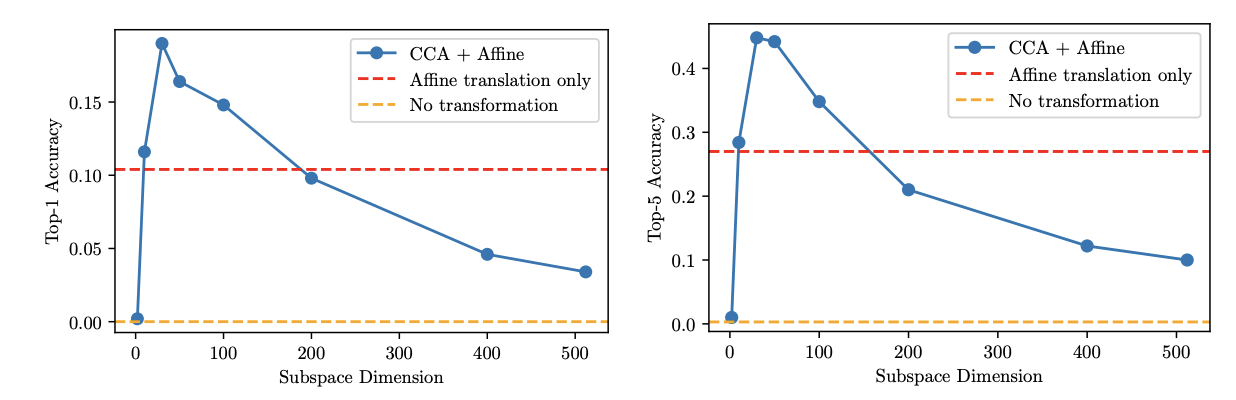
Importance of subspace projection (Ours)

위 실험결과를 바탕으로 본 논문에서는 CCA 기반으로 저차원 subspace을 먼저 추출한 뒤 alignment를 수행한다. validation set에서 subspace 차원에 따른 영향을 분석한 결과를 아래 그림에 나타낸다.

• Affine 정렬만 적용할 경우, 고차원 공간에서 더 나은 성능을 보이지만,
• Subspace projection을 적용한 경우, 차원이 낮을수록 더 나은 성능을 보인다.

이는 3D와 Text representation이 특정 저차원 space에서 더 잘 정렬된다는 가설을 뒷받침한다.

3D encoder complexity’s low impact on alignment.

예상대로 multimodal 3D 인코더가 모든 지표에서 가장 높은 성능을 기록하며, 상한선 역할을 한다.

그러나 흥미롭게도, unimodal 3D 인코더 중에서는 PointBERT가 SparseConv보다 더 좋은 성능을 보인다. 더 단순한 구조인 PointNet조차도 유사한 성능을 보인다.

이 결과는, 모델 복잡도만으로 정렬 성능이 결정되지 않는다는 것을 시사한다.

• 이는 Vision-Text alignment 분야에서는 복잡한 모델이 더 좋은 성능을 내는 경향이 있었던 것과 대조된다.
• 따라서, 3D-Text alignment에서는 모델 단순성이 오히려 정렬 해석력이나 표현 일관성을 높일 수도 있다.

Different alignment techniques have different strengths.

• Affine 변환 방식은 matching task에 특히 효과적이다.
• Local CKA 방식은 top-5 retrieval 정확도에서 더 뛰어난 성능을 보인다.

이는 각 기법이 서로 다른 방식으로 latent representation을 형성한다는 것을 의미하며, 향후에는 Hybrid alignment 방식이 유망한 방향이 될 수 있다.

Scaling of our approach.

Subspace 차원의 영향

위 그림에서는 subspace의 차원 수 d를 바꾸어가며 matching/retrieval 성능을 분석한다.

• 그 결과, subspace 정렬 방법은 차원이 낮을수록 성능이 더 우수하게 나타난다.
  • 예: d = 50일 때 가장 높은 성능을 달성함.
• 반면, Affine 변환만 사용하는 방식은 차원이 높을수록 오히려 성능이 더 좋다.

이는 3D와 텍스트 간의 유의미한 정렬은 저차원 부분공간에 집중되어 있다는 사실을 다시 한 번 확인시켜준다.

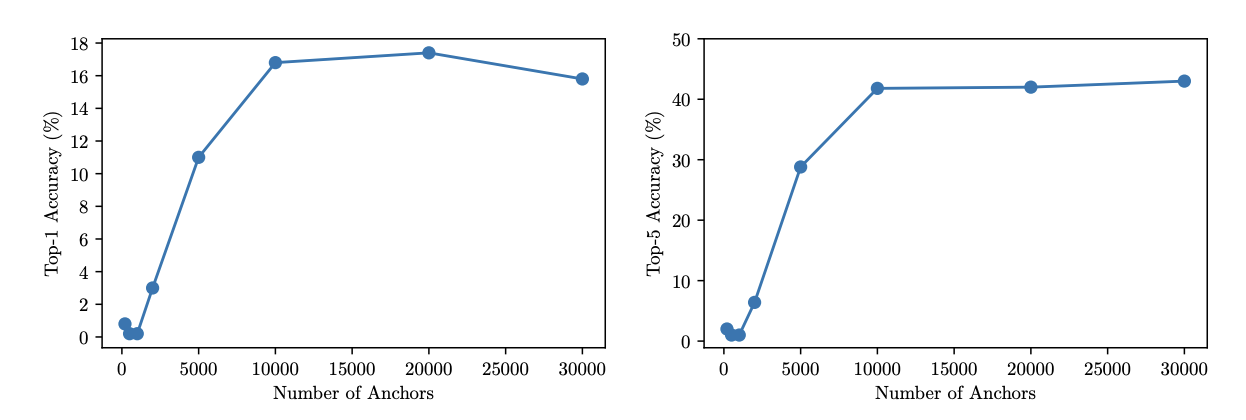
Anchor 수의 영향

아래 그림에서는 anchor 수를 변화시켜가며 성능 변화를 측정한다.

• anchor 수가 적을 때는 성능이 낮지만, 1만 개 이상부터 급격한 향상이 나타난다.
• 3만 개 이상부터는 성능이 정체되기 시작한다.

이는 subspace projection이 anchor 수에 민감하며, 어느 정도의 데이터를 확보해야 좋은 정렬이 가능함을 시사한다.

3. Geometries vs. semantics.

이 절에서는 정렬된 subspace가 갖는 semetic 특성을 분석한다.

즉, projection 공간이 geometry에 더 민감한지, 혹은 semantics에 더 집중하는지를 평가한다.

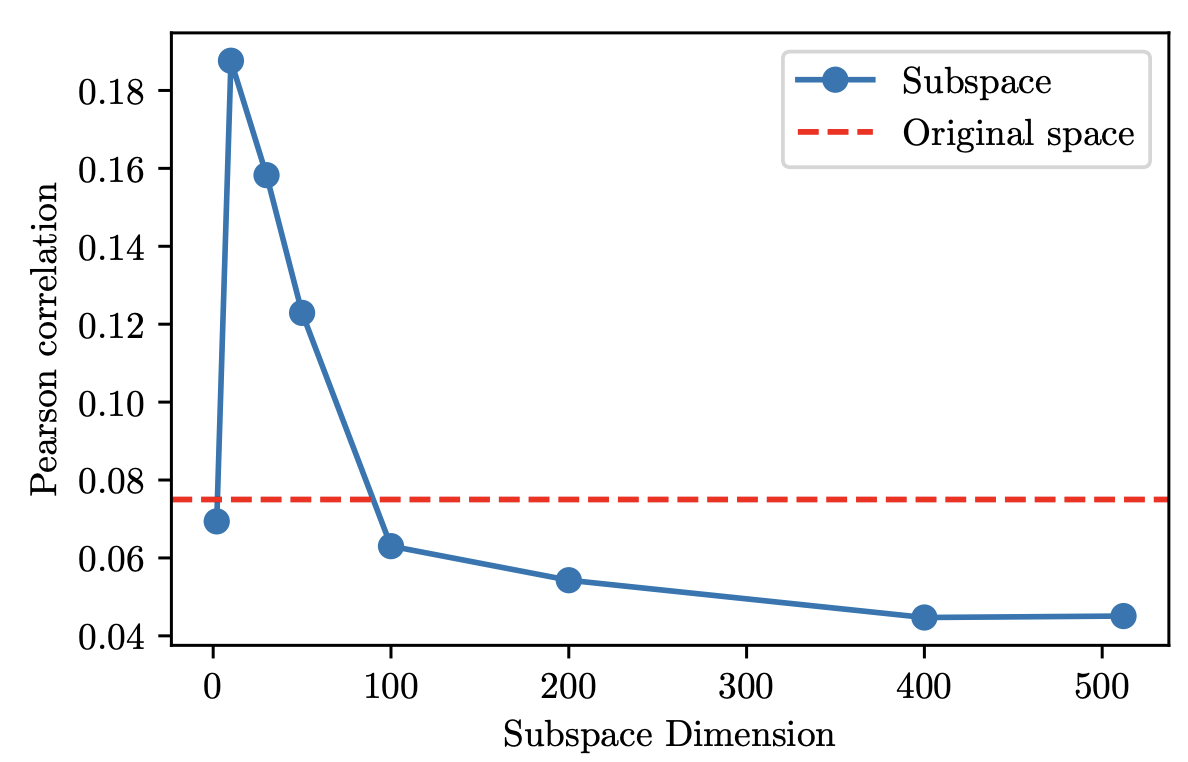
Geometric Awareness of 3D Latent subspace

정렬된 Te 임xt베딩과 Chamfer distance 간의 Pearson 상관계수를 계산한다. 그 결과, 정렬 전에는 거의 상관이 없었지만, 정렬 후에는 강한 음의 상관관계가 생긴다.

이는 Text representation이 정렬 후 3D의 기하학적 구조와 더 잘 대응되도록 변화했다는 것을 의미한다.

Semetic Understanding of Text Latent subspace

3D Point Cloud representation도 정렬 후에 의미적으로 유사한 텍스트와 더 잘 연결된다.

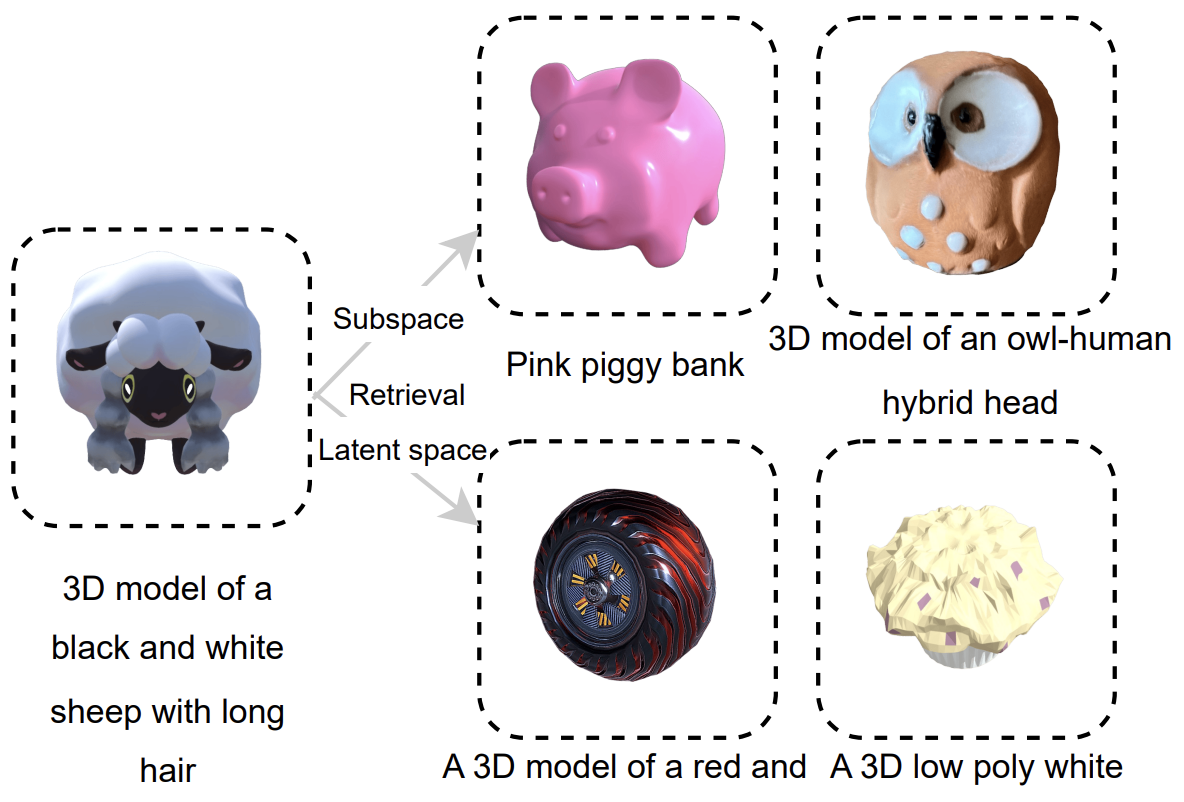
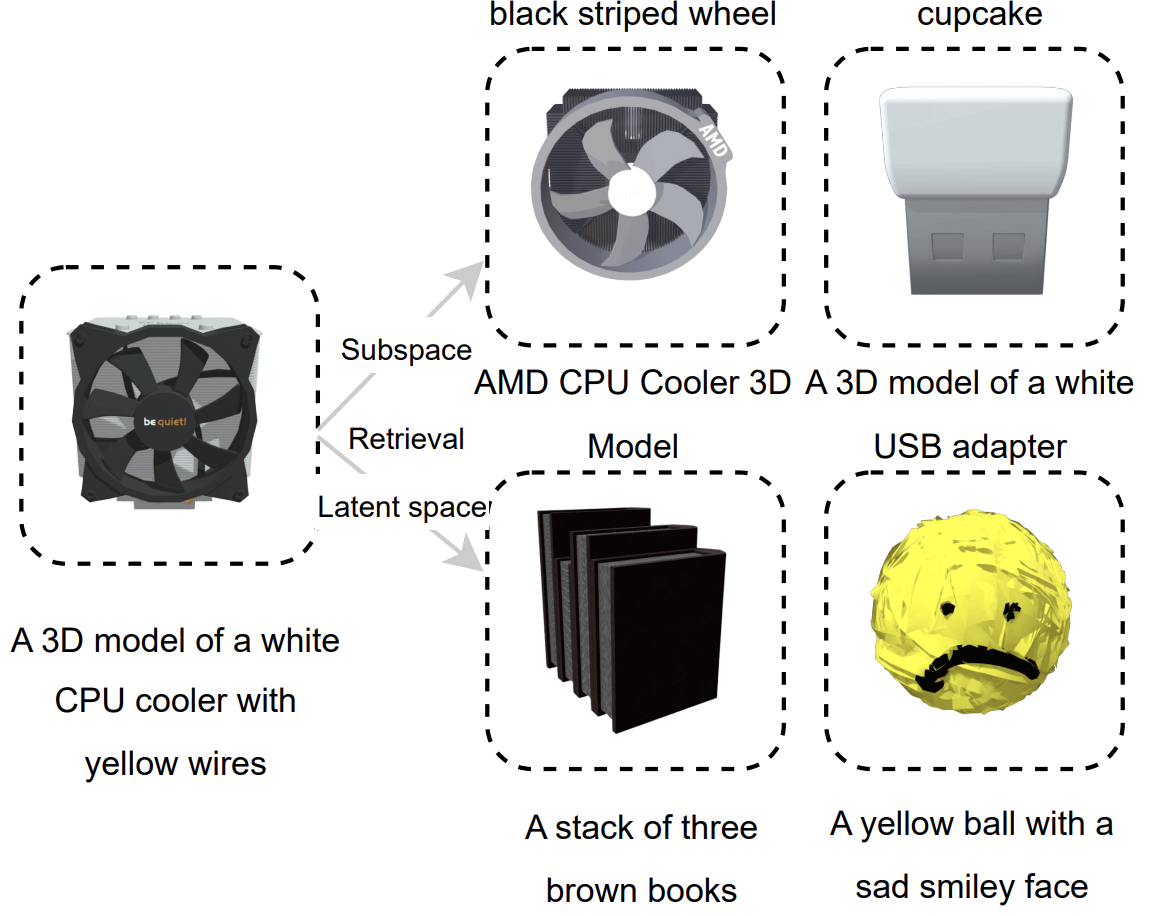
어떤 query shapes가 주어졌을 때, 아래 그림처럼

• subspace는 semetic하게 유사한 shape을 검색
• 원래 latent space는 geometric하게 유사한 shape을 검색

Conclusion

정렬되지 않은 상태의 latent representation만으로는 3D와 Text Encoder 간에 유사성을 거의 찾을 수 없다.

본 논문은, 저차원 subspace 정렬을 수행하면 의미 있는 연결이 가능해진다는 점을 보여준다.

이를 위해:

1. Canonical Correlation Analysis (CCA)를 사용하여 3D와 텍스트 간의 공통 subspace를 추출
2. 해당 공간에서 Affine 변환 또는 Local CKA를 통한 정렬 수행

그 결과:

• 정렬 전보다 최대 4배 향상된 성능을 달성하며, 모델 구조와 복잡성에 상관없이 일관된 성능 향상을 보인다.
• 정렬된 subspace는 geometric & memetic 정보가 상호 보완적으로 작용하는 representation space을 형성한다.

이 연구는 pretrained models간의 사후 정렬(post-hoc alignment)이 멀티모달 통합의 효과적인 경로가 될 수 있음을 시사한다.

Limitations

• 제한된 수의 3D 및 Text Encoder를 사용

• 정렬 가능한 표현이 주로 저차원 subspace에 존재

  → 복잡한 개념이나, 다중 객체 및 관계 정보가 필요한 장면(scene) 수준의 정렬에는 한계

~