[Paper Review] Flow Matching in Latent Space

[논문 리뷰] Flow Matching in Latent Space

Flow Matching in Latent Space

Quan Dao, Hao Phung

CVPR 2023

[Arxiv] [Github]

Flow Matching은 Diffusion에 비해 상대적으로 훈련하기 쉬우면서도 강력한 성능을 보여주는 생성 모델 알고리즘이다. 이 논문은 Flow matching 기법을 latent space에서 적용하는 방법을 제안한다.

Introduction

생성형 AI 분야에서 이전에는 고화질 이미지 생성을 위해 GAN이 널리 사용되었으며, 최근에는 Diffusion 모델이 주목받고 있다. 그러나 Diffusion 모델은 완벽하지 않으며 sampling 시간이 길다는 단점이 있다. 이를 해결하기 위해 sampling 효율을 향상시키려는 연구가 진행되고 있다.

Flow Matching은 source 분포(noise)에서 target 분포(생성된 sample)로의 경로를 따라가는 미분 방정식을 학습하는 것이다. ODE(상미분방정식) 기반인 Flow Matching은 SDE(확률미분방정식) 기반 Diffusion 모델에 비해 훈련이 더 쉽고 Sampling 속도가 빠르다는 이점이 있다. 이 논문에서는 Flow matching에 Diffusion에 적용했던 다음과 같은 기법을 적용한다.

1. 픽셀 space에서 수행했던 Flow matching을 latent space에서 적용
2. class labels, segmentation masks, 이미지 등 다양한 조건부 입력을 지원
3. 재구성된 latent flow 분포와 실제 데이터 분포 사이의 Wasserstein-2 거리가 Latent Flow matching objective에 의해 상한이 정해져 있음을 보여준다.

Background

Continuous Normalizing Flow

CNF란 단순한 분포(예:Noise)를 복잡한 분포(예:고양이 이미지)의 데이터로 변환하는 수학적 도구이다.

이렇게 데이터 분포가 어떻게 변화하는지를 나타내는 것이 확률 밀도 경로(Probability Density Path) $p_t(x)$이며 $\int p_t(x)dx = 1$이다. 각 시간 t마다 각 데이터가 target 분포로 어디로, 얼마나 빠르게 이동해야 하는지 나타내는 지도, 함수가 Vector field $v_t$이고, 이 $v_t$를 따라 이동한 $t$ 까지의 경로를 flow $\phi$ 라고 한다.(ODE로 정의) 즉, 초기 data point $x$라 할때, $\phi_0(x) = x$ 이다.

\[\frac{d}{dt}\phi_t(x) = v_t(\phi_t(x))\]

여기서 Vector field $v_t$를 신경망 $v_t(x:\theta)$로 모델링한 것이 CNF이며 연속적인 $t$변화에 따른 데이터 변환을 모델링한다. CNF는 push-forward 방정식을 통해 단순한 $p_0$에서 복잡한 $p_1$로 변환하는데 사용된다.

\[p_t = [\phi_t]*p_0\]

하지만 CNF 학습 프레임워크는 매 iter마다 ODE를 풀어야하기 때문에 cost가 많이 든다.

CNF에서 연속적인 시간에 따른 흐름을 계산하기 위해서 ODE을 직접 풀기는 어렵다. 모델이 아주 작은 timestep별로 변화를 계산하면서 근사하는 방식을 사용하는데, 각 학습의 단계마다 이를 수행해야 하고 정확한 결과를 위해 아주 작은 시간 간격으로 계산해야 하므로 cost가 많이 드는 것이다.

Flow Matching(FM) & Conditional FM

앞선 CNF처럼 학습 중에 ODE를 푸는게 아니라, Regression기반 Objective function을 사용하여 target vector field $u_t$와 매칭한다.

\[\mathcal{L}_\text{FM}(\theta) = \mathbb{E}_{t,p_t(x)} \left\|v_t(x)-u_t(x) \right\|^2\]

이 loss가 0이 되면 CNF 모델 $p_t(x)$가 만들어지지만, $u_t$와 $p_t$에 대한 정보가 없기 때문에 condition을 추가하여 계산을 단순화한다.

Conditional FM

\[\mathcal{L}_\text{CFM}(\theta) = \mathbb{E}_{t,q(x_1),p_t(x|x_1)} \left\|v_t(x)-u_t(x|x_1) \right\|^2, \;\; t \sim \mathcal{U}[0,1],\;\;x_1\sim q(x_1), \;\;x\sim p_t(x|x_1)\]

FM과 달리 CFM은 표본 $x_1$별로 정의되어있기 때문에 Gaussian 조건부 확률 경로 $p_t(x|x_1)$를 정의한다.

\[p_t(x|x_1) = \mathcal{N}(x|\mu_t(x_1), \sigma_t(x_1)^2I)\]

이 $p_t$를 생성하기 위해 조건부 벡터 필드가 필요하지만 무수히 많은 벡터 필드 중 가장 간단한 형태를 사용한다. 이때의 Flow를 $\psi$라 하면 다음과 같다.

\[\psi_t(x) = \sigma_t(x_1)x + \mu_t(x_1)\] \[\frac{d}{dt}\psi_t(x) = u_t(\psi_t(x)|x_1)\]

$\psi_t$는 위 식으로도 알 수 있듯이 affine(선형) 변환이며, target vector field를 계산할 수 있어서 위 $\mathcal{L}_\text{CFM}$에 대입할 수 있다.

Diffusion model

CNF에서는 ODE로 데이터 분포를 정의하는 반면, Diffusion model은 stochastic한 과정으로, Score-based model을 기반으로 한다. 이는 SDE를 사용하여 noise 분포에서부터 denoising하여 확률 경로를 찾는다. Stochastic하기 때문에 sample을 생성하기 위해 수많은 과정을 거쳐야하며 계산 cost가 많이 든다. 이러한 단점 때문에 AutoEncoder의 latent space(LDM)를 활용하기도 하고, deterministic한 sampler(DDIM)를 사용하여 계산의 효율성을 높인다.

Flow Matching과 Diffusion의 차이점은 다음과 같다.

1. FM은 Linear interpolation, Diffusion은 noise scheduler에 의존한다.
2. Sampling에서 Diffusion은 stochastic하게 움직이지만, FM은 deterministic한 경로로 작동하여 무작위성이 적다.

이 논문에서는 Latent representation을 FM에 사용하는것이 자기들이 처음이라고 말한다.

Detail

데이터 분포 $x_0 \sim p_0$와 noise 분포 $x_1 \sim p_1$에서, Flow Matching의 목표는 두 분포 사이의 변화를 설명하는 결합$\pi(p_0, p_1)$을 추정하는 것이다. 이는 다음과 같은 미분 방정식을 풀어서 달성할 수 있다:

\[\text{d}x_t = v(x_t, t)dt, \tag{1}\]

여기서 시간 $t \in [0, 1]$ 동안, 속도 $v : \mathbb{R}^d \times [0, 1] \rightarrow \mathbb{R}^d$는 $p_0$에서 $p_1$로의 flow를 이끈다. 이 $v$는 FM loss에서 $\theta$로 parameterize된 vector field가 되며 $\theta$는 다음과 같이 추청할 수 있다.

\[\hat{\theta} = \arg\min_\theta \mathbb{E}_{t,x_t} \left[ \|v(x_t, t) - v_\theta(x_t, t)\|^2_2 \right]. \tag{2}\]

이 추정을 통해, 우리는 역 샘플링을 수행할 수 있다. 즉, $x_0$은 $x_1 \sim p_1$에 접근할 수 있으며, 적분을 풀어 $x_0$를 구할 수 있다. (1)번 ODE는 Lagrangian flow로 불리며, 이는 point clouds의 동역학을 설명한다. 우리는 유사한 Eulerian 형식의 연속 방정식을 가지고 있으며, 이는 측정의 동역학을 설명한다:

\[\partial_t pt = -\text{div}(v(x, t)p_t), \tag{3}\]

여기서 $\text{div}$는 발산 연산자이다. 위 방정식 (2)은 $v(x, t)$에 대한 다양한 옵션을 포함할 수 있으며, 이는 Flow Matching의 유연성을 강조한다. 다음에서는 $v(x, t)$의 두 가지 널리 사용되는 변형에 대해 소개한다.

Probability flow ODE

Probability flow ODE에서 $v$는 다음과 같은 형태를 가진다.

\[v_t(x_t, t) = f(x_t, t) - \frac{g^2_t}{2} \nabla \log p_t, \;\; \tag{4}\]

여기서 $\nabla \log p_t$는 Score function, $f(x_t, t)$와 $g_t$는 각각 Diffusion process, 즉 SDE의 드리프트 및 diffusion 계수이다.

\[\textbf{SDE} \;\;\;\;\text{d}x_t = f(x_t, t)\text{d}t + g_t\text{d}w \tag{5}\]

여기서 $w$는 브라운 운동dl다. 그러면 Flow Matching은 Score matching loss로 다시 표현될 수 있다. 일반적인 경로 $x_t$는 분산 보존(VP) 경로이다:

\[x_t \stackrel{\text{def}}{=} \alpha_t x_0 + (1 - \alpha^2_t)^{1/2} x_1, \text{ where } \alpha_t = e^{-\frac{1}{2} \int_0^t \beta(s)ds}. \tag{6}\]

앞선 연구에서는 (4)의 ODE sampler와 경로 (6)를 사용하면 Diffusion SDE 식 (5)와 비교하여 샘플링 비용을 줄일 수 있음을 보여준다.

Constant velocity ODE

또다른 연구에서는 VP Probability flow ODE에서 (6)의 비선형 보간을 사용하는 것이 생성 궤적의 곡률을 불필요하게 증가시킬 수 있다고 지적했으며 이는 훈련 및 샘플링 효율을 감소시킬 수 있다. 대신, 그들은 Constant velocity(상수 속도) ODE를 사용하는 것을 제안하며, 이는 x0과 x1 사이의 선형 보간을 의미한다. 이는 속도가 흐름을 따라 $v_t = x_1 - x_0$ 방향으로 이끈다는 것을 의미하고, Flow Matching 손실은 다음과 같이 된다:

\[\hat{\theta} = \arg\min_\theta \mathbb{E}_{t,x_t} \left[ \|x_1 - x_0 - v\theta(x_t, t)\|^2_2 \right].\]

따라서 논문에서는 위와같은 프레임워크를 사용하여 train하고, (1)의 ODE를 사용하여 샘플링을 개발한다.

Method

이 섹션에서는 먼저 제안한 프레임워크의 train 및 sampling를 소개한 다음, class conditional generation을 위한 classifier-free 속도 필드를 제시한다.

vector field == velocity field

1. Training and sampling procedure

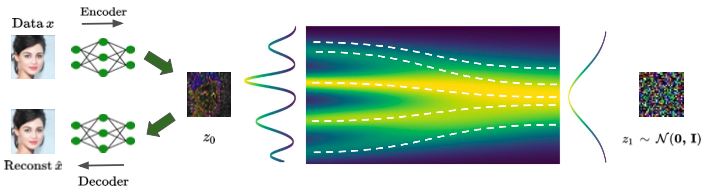
입력 샘플 $x_0 \sim p_0$이 주어지면, 이를 VAE로 인코딩하여 latent vector $z_0 = E(x_0) \in \mathbb{R}^{d/h}$를 생성한다. 여기서 $h$는 VAE의 downsampling ratio이다. 이 latent space에서의 목표는 noise $z_1 \sim \mathcal{N}(0, I)$에서 latent vector의 source 분포 $z_0$로의 확률 경로를 추정하는 것이다.

속도 $v$의 최적화는 latent space에서 Constant velocity의 vanilla flow matching objective을 사용하며, condition $c$를 포함시켜 conditional latent flow matching을 학습한다.

\[\hat{\theta} = \arg\min_\theta \mathbb{E}{t,zt} \left[ \|z_1 - z_0 - v\theta(zt, c, t)\|^2_2 \right].\]

마지막으로, 샘플 $\hat{z}$ 는 pertained VAE decoder $D$로 디코딩되어 출력 이미지 ${\hat{x}} = D({\hat{z}})$를 생성한다.

2. Conditional generation with classifier-free guidance for velocity field

GAN과 Diffusion에서 처럼 Flow matching의 ODE sampler에 class label $c$를 통합한다.

Diffusion Models Beat GANs on Image Synthesis에서는 guidance를 주기 위해 pretrained Classifier $p(c|x)$를 사용했다. 하지만 pipeline이 복잡해지고, 이 Classifier는 $x_t$가 noise가 있는 상황에서 학습되어야 하기 때문에 pretrained Classifier를 원활하게 통합하는 것이 어렵다. 따라서 Classifier-Free Diffusion Guidance처럼 Classifier-free 속도 field를 위한 공식을 제안한다.

먼저, SDE 방정식 (5)를 Fokker-Planck 방정식으로 다시 쓸 수 있다:

\[\partial_t \tilde{p}_t = -\text{div}(f(x_t, t)\tilde{p}_t) + \frac{g_t^2}{2} \Delta \tilde{p}_t,\]

여기서 $\tilde{p}_t \stackrel{\text{def}}{=} p_t(x_t|x_0, c)$는 label $c$의 조건부 확률이다. 이를 연속 방정식의 형태 (3) 로 변환할 수 있다.

\[\partial_t \tilde{p}_t = -\text{div} \left[ \left(f(x_t, t)p_t - \frac{g_t^2}{2} \frac{\nabla \tilde{p}_t}{\tilde{p}_t} \right) \tilde{p}_t \right] = -\text{div} \left[ \left(f(x_t, t) - \frac{g_t^2}{2} \nabla \log \tilde{p}_t \right) \tilde{p}_t \right].\]

이는 수정된 속도 벡터가 다음과 같은 형태를 가짐을 암시한다.

\[\tilde{v}(x_t, t) = f(x_t, t) - \frac{g_t^2}{2} \nabla \log \tilde{p}_t = f(x_t, t) - \frac{g_t^2}{2} (\nabla \log p_t + \nabla_x \log p(c|x_t)), \tag{12}\]

여기서 $\tilde{p}_t=p_t(x_t|x_0, c) = Zp_t(x_t|x_0)p(c|x_t)$라고 할 수 있으며, $Z$는 log-likelihood의 gradient를 취한 후 무시할 수 있는 정규화 상수이다.

VP ODE와 마찬가지로 상수 속도 경로 $x_t = (1− t)x_0 + tx_1$는 $N(x_t; (1− t)x_0, t^2I)$를 따르며, 다음을 얻는다:

\[\nabla_x \log p_t = -\frac{(x_t - (1− t)x_0)}{t^2}, \quad f(x_t, t) = -\frac{x_t}{1− t}, \quad \frac{g_t^2}{2} = \frac{t}{1− t}.\]

이를 (12)에 대입하면, Classifier에 의해 안내된 속도 필드는 Diffusion Models Beat GANs on Image Synthesis과 유사하게 된다:

\[\tilde{v}(x_t, c, t) = v_\theta(x_t, t) - \gamma \left(\frac{t}{1− t}\right) \nabla_x \log p(c|x_t), \tag{14}\]

여기서 $\gamma > 0$은 gradient 강도를 조절한다. 최종적으로, Classifier-free를 위해, 먼저 입력으로 condition $c$를 추가하고, $v_\theta(x_t, c, t)$로 표기한다. 그런 다음 Bayes rule을 사용하여 (14)의 $\nabla_x \log p(c|x_t)$ 를 $\nabla_x \log p(x_t|x_0, c) - \nabla_x \log p(x_t|x_0)$로 분해하면 다음과 같다:

\[\begin{align} \tilde{v}(x_t, c, t) &= v_\theta(x_t, t) - \gamma \left(\frac{t}{1− t}\right) \nabla_x \log p(c|x_t) \\ &= v_\theta(x_t, t) - \gamma \left(\frac{t}{1− t}\right) (\nabla_x \log p(x_t|x_0, c) - \nabla_x \log p(x_t|x_0)). \tag{15} \end{align}\]

수식 (4)를 사용하여 $-v_t(x_t, c, t) + f(x_t, t) = \frac{g_t^2}{2} \nabla \log p_t(x_t|c)$을 얻으며, $x_t$가 고정되고 $f, g$가 정의된 함수이기 때문에 다음을 얻는다:

\[\begin{align} \frac{g_t^2}{2} (\nabla \log pt(x_t|c) - \nabla \log p_t(x_t|c = \emptyset)) &= -v_t(x_t, c, t) + f(x_t, t) + v_t(x_t, c = \emptyset, t) - f(x_t, t) \\ &= -v_t(x_t, c, t) + v_t(x_t, c = \emptyset, t). \tag{16} \end{align}\]

이를 (15)에 대입하면, 다음을 근사할 수 있다:

\[\tilde{v}_\theta(x_t, c, t) \approx v\theta(x_t, t) + \gamma(v_\theta(x_t, c, t) - v_\theta(x_t, t)) = \gamma v_\theta(x_t, c, t) + (1− \gamma)v_\theta(x_t, c = \emptyset, t),\]

여기서 $v_\theta(x_t, t) = v_\theta(x_t, c = \emptyset, t)$는 $c$가 없는 uncondition으로 훈련된 것을 나타낸다. 이를 통해 하나의 신경망 내에서 unconditional 모델과 conditional 모델을 함께 훈련할 수 있다.