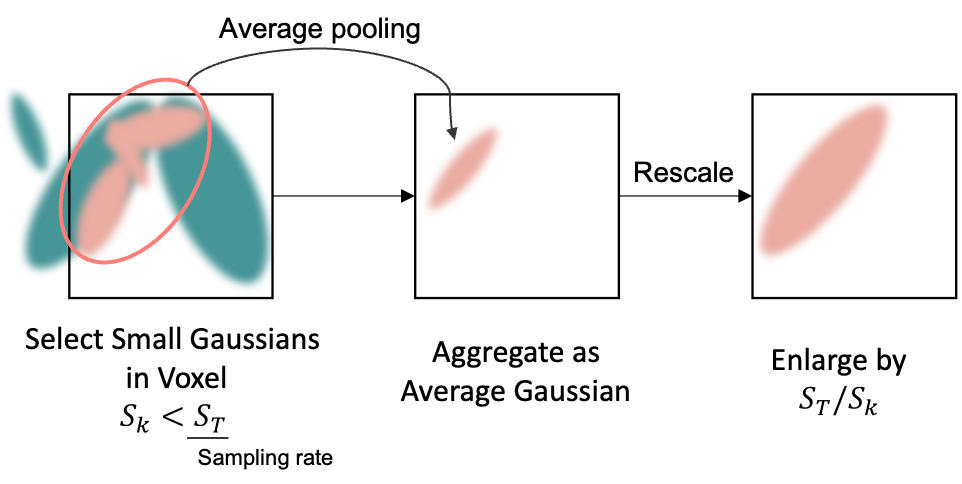[Paper Review] Multi-Scale 3D Gaussian Splatting

[논문 리뷰] Multi-Scale 3D Gaussian Splatting for Anti-Aliased Rendering

Multi-Scale 3D Gaussian Splatting for Anti-Aliased Rendering

Zhiwen Yan, Weng Fei Low, Yu Chen, Gim Hee Lee

CVPR 2024.

[Arxiv] [Project Page] [Github]

Introduction

3D Gaussian Splatting은 새로운 시점에서의 이미지 합성을 위한 효율적인 방법으로 최근 주목받고 있지만, 이 rasterization 알고리즘은 낮은 해상도에서나 멀리 떨어진 위치에서 동일한 장면을 렌더링할 때 심각한 Aliasing artifact와 속도 저하의 문제를 겪게 된다.

Aliasing artifact

Aliasing artifact란 sampling rate가 continuous 신호를 정확하게 포착하지 못해 정보의 손실이 일어나는 현상이다.

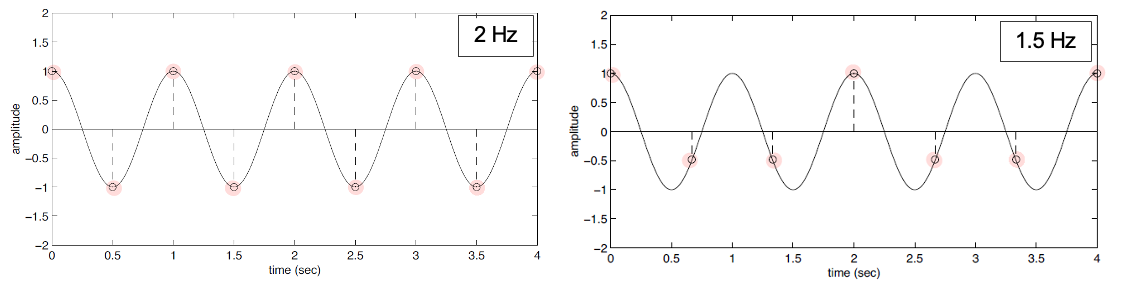
Nyquist 이론은 이러한 aliasing을 방지하는 것으로, 원래 주파수의 2배 이상으로 sampling을 해야 Aliasing 이 발생하지 않는다는 것을 말한다.

위 그림을 보면, 원래 continous한 신호의 주파수는 1Hz이며, 2Hz이상의 sampling rate로 sampling을 진행하였을 때 원래의 정보를 잃어버리지 않는 것을 볼 수 있다.

3D Gaussian의 rasterization에서는 3D Gaussian의 집합을 2D 이미지로 투영할 때, 2D이미지의 pixel이 sampling rate가 된다.

Gaussian들 표현해야할 Pixel수가 적으면(= 해상도가 낮아지면) 수많은 Gaussian을 충분히 표현하지 못한다.

또한, 또한 3D Gaussian Splatting은 $16 \times 16$ 픽셀 크기의 tile 단위로 병렬 처리를 수행하는데,

해상도가 낮아지면 tile 수는 감소하고, 해당 tile이 포함하는 Gaussian 수는 많아지기 때문에 Rendering 시간이 오히려 증가한다.

Method

Multi-Scale Gaussian Splatting에서는 크게 2가지 method를 제안한다.

1. 기존의 Gaussian을 크게 만드는 것

2. Rendering과정에서 2D 해상도에 따라 Gaussian을 선택적으로 투영하는 것

$1\times$, $4\times$, $16\times$, $64\times$로 downsampling된 4가지 level의 해상도로 method를 수행한다.

작고 세밀한 레벨의 Gaussian들은 훈련 동안 큰 Gaussian을 생성하기 위해 집계됩니다. 각 3D Gaussian $\mathcal{G}_{k}^{l}$은 하나의 레벨 $l$에 속하며, 렌더링 시 그것의 Pixel Coverage에 따라 독립적으로 포함되거나 제외됩니다.

Pixel Coverage

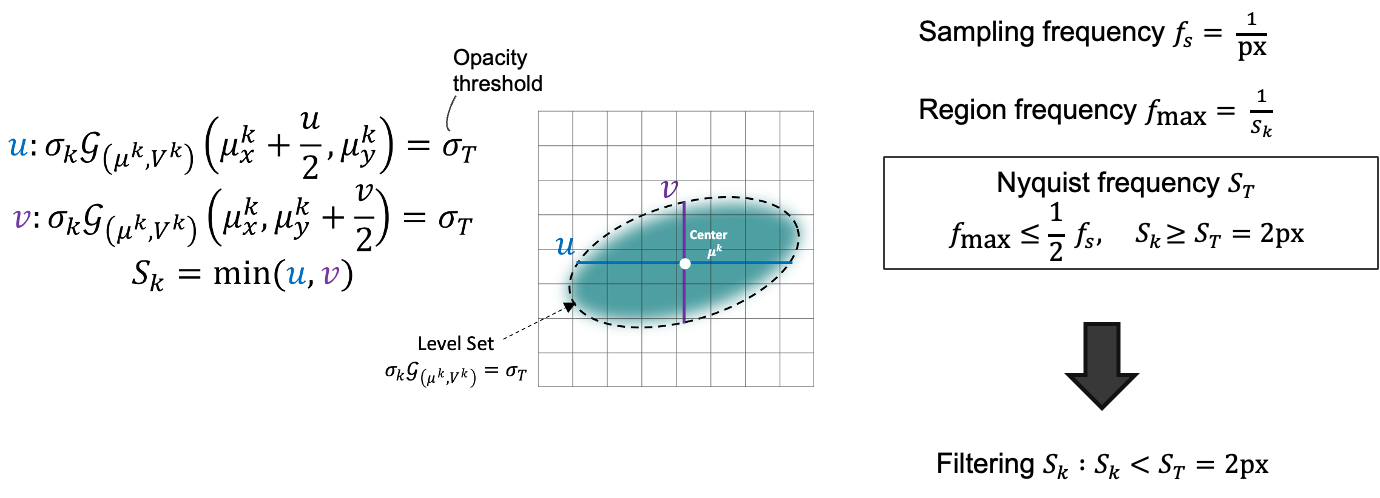
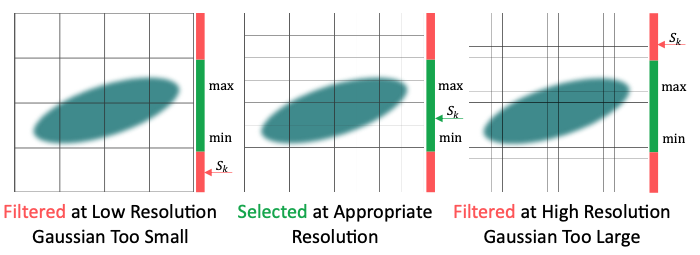
Gaussian의 “Pixel Coverage”는 window space에 splatting되었을 때, Gaussian의 크기가 현재 렌더링 해상도의 픽셀 크기와 비교하여 반영된 것을 나타낸다.

스플래팅된 2D Gaussian $\mathcal{G}_{(\mu^k, V^k)}$의 Pixel Coverage $S_k$는 그것의 수평/수직 축의 길이 중 작은 것으로, 불투명도 임계값 $\sigma_T = \frac{1}{255}$까지 측정되며, 이는 그림에서 보여진다.

변수 설명:

​ • $\mu^k_x, \mu^k_y$ : Gaussian 중심 위치

​ • $u, v$ : 각각 Gaussian이 확장되는 수평 및 수직 방향의 반경

​ • $\sigma_T$ : 임계 불투명도 값

​ • $\sigma_k$ : Gaussian의 불투명도 값

​ • $G(\mu_k, v_k)$ : 중심이 $\mu_k$이고 공분산 행렬이 $v_k$인 2D Gaussian 함수

식의 의미:

​ $\sigma_k G(\mu_k, v_k)(\mu_x^k + \frac{u}{2}, \mu_y^k) = \sigma_T$, $\sigma_k G(\mu_k, v_k)(\mu_x^k, \mu_y^k + \frac{v}{2}) = \sigma_T$

이 부분은 Gaussian 함수에서 $u$와 $v$ 방향으로 $\frac{u}{2}$, $\frac{v}{2}$만큼 이동했을 때 불투명도 값이 $\sigma_T$에 도달하는 지점을 찾는 것이다. 이를 통해 Gaussian이 Window 상에서 얼마나 넓게 퍼져 있는지를 수치적으로 측정할 수 있습니다.

즉 $S$가 크면 해당 픽셀은 이 Gaussian이 많이 차지한다는 뜻이고, 이는 해당 Gaussian이 나타내는것은 Detail이 없는 저주파 영역이라는 것이다.

Pixel Coverage $S_K$가 Nyquist frequncy인 $S_T$ 보다 작으면 해당 영역은 픽셀이 표현하기에는 Detail이 많은 고주파 영역이고, 이는 Aliasing이 일어난다는 것이다.

따라서 Pixel Coverage $S_k < S_T = 2\mathrm{px}$인 Gaussian은 렌더링 중에 필터링되어야 한다.

하지만, 3D Gaussian 표현은 다른 주파수의 신호를 다른 Gaussian에 인코딩하지 않기 때문에, 작은 Gaussian을 단순히 필터링하는 것은 장면에서 구멍이나 누락된 부분을 초래할 수 있다.

이 문제를 해결하기 위해, 작은 Gaussian을 집계하여 저주파 신호를 인코딩하는 큰 Gaussian을 형성할 것을 제안한다.

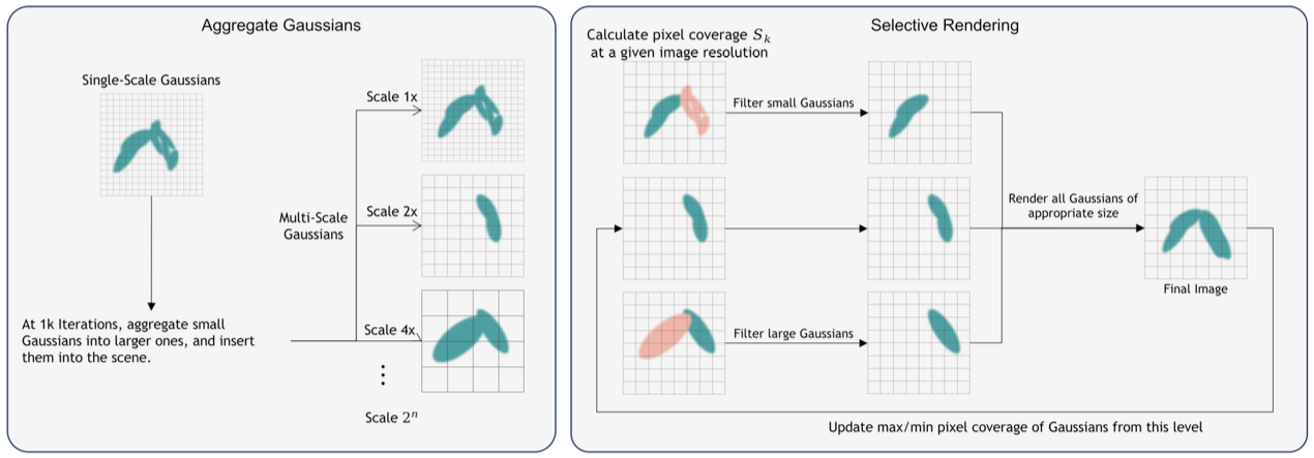
Aggregate to Insert Large Gaussians

train 시작 시 input Point Cloud에서 초기화된 모든 3D Gaussian들은 가장 세밀한 레벨 $l=1$에 속한다. 처음 1,000 iteration의 워밍업 단계 후에, 너무 작은 세밀한 레벨의 Gaussian을 집계하여 더 큰 레벨의 Gaussian을 도입한다.

1. 모든 레벨 ${l_m \mid 2 \le l_m \le l_{max}}$에 대해, 우리는 모든 train 이미지의 $4^{l_m-1}$ 배 다운샘플된 해상도에서 $[1,l_m-1]$의 모든 3D Gaussian을 렌더링한다. 
1. 해상도에 따른 $S_T$보다 최소 Pixel Coverage $S_k$가 작은 모든 3D Gaussian들이 선택된다.

1. 선택된 3D Gaussian은 그들의 위치에 기반하여 $(400/l_m)^3$ 해상도의 Voxel grid에 집합되며, 각 Voxel 내 모든 Gaussian의 속성은 새로운 Gaussian을 생성하기 위해 Average Pooling을 사용하여 합쳐진다.

2. 각 Voxel 내 Gaussian들의 평균 Pixel Coverage $S_{avg}$에 기반하여 생성된 각 새로운 Gaussian은 $S_T/S_{avg}$ 만큼 확대되며 레벨 $l_m$에 속한다.

위의 절차는 작은 Gaussian들이 생성하는 문제를 방지하고, 렌더링 과정에서 더 큰 Gaussian들이 필요한 곳에 효율적으로 대응할 수 있도록 한다. 이 접근 방식은 장면의 다양한 해상도에서의 세밀한 조절을 가능하게 하며, 더 큰 Gaussian들을 적절하게 활용하여 전체적인 품질을 향상시키는 데 기여한다.

Selective Rendering

큰 Gaussian이 추가된 후, 모델은 원본 이미지와 downsampling 이미지 모두를 사용하여 훈련됩니다. 각 Gaussian의 최대 픽셀 커버리지 $S_k^{max}$와 최소 픽셀 커버리지 $S_k^{min}$는 Selective Rendering을 위해 저장됩니다. 렌더링 downsampling scale이 Gaussian $\mathcal{G}_k$이 생성될 때의 downsampling scale과 같다면, 그것의 $S_k^{max}$와 $S_k^{min}$ 값은 새로운 픽셀 커버리지 $S_k$로 업데이트된다:

\[\begin{aligned} S_k^{max} &= \max(\lambda_1 S_k^{max}, S_k), \\ S_k^{min} &= \min(\lambda_2 S_k^{min}, S_k), \end{aligned}\]

여기서 $\lambda_1$과 $\lambda_2$는 각각 $0.95$와 $1.05$의 경험적 값인 감쇠 계수이다.

렌더링은 어떤 해상도나 카메라 거리에서도 진행될 수 있으며, Gaussian은 화면상에서의 픽셀 커버리지 $S_k$가 다음 조건을 만족할 때 렌더링을 위해 선택된다: \(\left(\frac{S_k}{S_k^{max}} \leq S_{rel}^{max}\right) \land \left(\frac{S_k}{S_k^{min}} \geq S_{rel}^{min} \lor S_k \geq S_T\right),\)

여기서 $S_{rel}^{max}$와 $S_{rel}^{min}$은 각각 최대 및 최소 상대 픽셀 커버리지로, $1.5$와 $0.5$의 경험적 값이다. Gaussian의 픽셀 커버리지가 $S_k^{max}$보다 훨씬 크면 렌더링에서 필터링된다. 마찬가지로, 그것이 $S_k^{min}$보다 훨씬 작고 $S_T$보다 작으면 렌더링에서 필터링된다.

절대 $S_T$ 임계값은 화면 크기가 충분히 작지 않으면 Aliasing 문제를 일으키지 않는 하위 스케일의 큰 Gaussian을 보존하는 데 사용된다. (아래 알고리즘 2)

가장 높은 해상도에서 최대 훈련 해상도를 초과하고 최소 훈련 해상도 아래에서 렌더링하는 경우, 가장 세밀한 레벨의 Gaussian들이 너무 크거나 가장 조잡한 레벨의 Gaussian들이 너무 작더라도 필터링되지 않는다.

각 Gaussian의 픽셀 커버리지 범위는 모델이 다양한 세부 수준의 Multi-Scale Gaussian을 유지할 수 있게 한다. 다양한 해상도와 거리에서 렌더링을 위한 적절한 Gaussian 하위 집합이 선택됩니다. 고해상도에서는 고주파 정보를 인코딩하는 더 많은 작은 Gaussian이 렌더링되고, 저해상도에서는 Aliasing 효과를 줄이고 속도를 높이기 위해 저주파 정보를 인코딩하는 더 적고 큰 Gaussian이 렌더링된다.

Evaluation

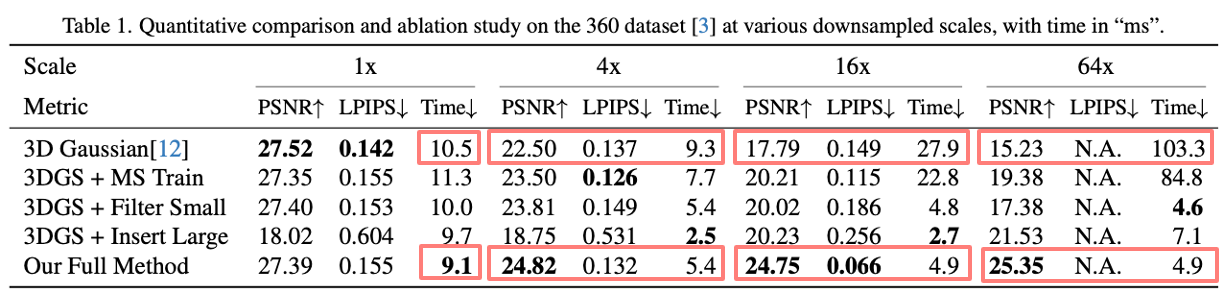
고해상도에서는 원래 Gaussian 스플래팅의 품질이 더 좋지만, 해상도가 내려갈수록 정량적 지표의 차이는 더 벌어지며 이 논문의 이미지 품질이 더 좋아진다.

또한 렌더링 시간 역시 해상도가 낮아질수록 오래걸리는 오리지널에 비해 이 방법은 시간이 단축되고있음을 알 수 있다.

하지만 저해상도에서 렌더링할 때 일부 가우시안만 사용하더라도, Splatting은 모든 가우시안을 해야하기 때문에 선형적으로 시간이 단축되지 않는 이유는 이때문이다.