[Paper Review] Stable Diffusion 3

[논문 리뷰] Scaling Rectified Flow Transformers for High-Resolution Image Synthesis

Visual Representation Alignment for MLLMs

Patrick Esser, et al

ICML 2024

[arXiv] [Github] [Hugging Face]

Background

Rectified Flow (RF)

Rectified Flow는 데이터 분포에서 noise 분포까지 직선 경로(straight line)로 연결하는 생성 모델 정식이다.

일반적인 확산(diffusion) 모델이 데이터에 점진적으로 noise를 추가하는 곡선 경로(확률적 과정)를 따른다면, Rectified Flow는 처음부터 끝까지 직선 경로를 가정하여 forward 과정을 정의한다.

이를 통해 이론적으로 단일 step으로도 데이터 → noise 변환을 시뮬레이션할 수 있는 장점이 있지만, 아직까지 실용적 표준으로 확립되지는 못했다.

최근 중소규모 실험에서 Rectified Flow의 이점(특히 class-conditional 생성에서의 효율성)이 일부 확인되었으나 , 대규모 텍스트-이미지 합성에서는 널리 활용되지 않았다.

본 논문은 이러한 Rectified Flow를 대규모 텍스트-투-이미지 생성에 적용하여 성능을 끌어올리고자 한다.

Classifier-Free Guidance (CFG)

Classifier-Free Guidance는 이미지 생성 품질을 향상시키기 위해 조건부 diffusion model에서 활용되는 기법으로, 조건(prompt)을 사용한 예측과 무조건(unconditional) 예측을 혼합하여 생성 방향을 조절한다.

특히 텍스트-투-이미지 diffusion model에서, 주어진 프롬프트에 대한 정확한 묘사를 얻기 위해 모델의 출력 $\epsilon_\theta(x \mid \text{prompt})$와 프롬프트를 빈 문자열 등으로 대치한 출력 $\epsilon_\theta(x \mid \varnothing)$를 결합한다.

일반적으로 최종 sampling 단계에서 모델 입력에 $w$라는 guidance 스케일을 적용하여 두 출력을 $(1+w)\epsilon_\theta(x \mid \text{prompt}) - w,\epsilon_\theta(x \mid \varnothing)$ 형태로 가중 합함으로써, 프롬프트 준수도를 높이면서도 다양성 감소를 완화한다.

SD3 모델의 실험에서도 1.0, 2.5, 5.0 등 다양한 guidance 스케일을 적용하여 생성 성능을 비교하고 있다 .

EDM (Elucidated Diffusion Model)

EDM은 Karras 등 이 제안한 diffusion model 일정(schedule)로, 로그 신호대잡음비(log-SNR) 관점에서 최적화된 noise 스케줄을 도입한 기법이다.

기존 DDPM의 선형 schedule이나 Cosine schedule과 달리, EDM은 $\sigma(t)$ (noise 표준편차)를 데이터-noise quantile 함수로 정의하여 각 시점마다 효과적인 학습 신호 균형을 맞춘다.

이를 통해 훈련 시 특정 구간의 중요도를 높이고, 개선된 F-예측 loss 함수와 함께 sampling 효율 및 이미지 품질을 향상시킨 것으로 알려져 있다 (예: StyleGAN-형 가우시안 분산 사용).

본 논문에서는 EDM을 diffusion model의 한 변형으로 간주하여 Rectified Flow와 성능을 비교하고, 또한 EDM의 로그-SNR 가중치를 Rectified Flow에 접목한 변형도 실험적으로 평가한다 .

Introduction

이 논문은 Rectified Flow와 Transformer 기반 듀얼 스트림 아키텍처를 결합하여, 대용량의 고해상도 텍스트-투-이미지 생성에서 SOTA의 성능을 달성한 연구이다.

이들은 noise 스케줄링 기법 개선과 모달리티별 분리된 Transformer 설계를 통해, 적은 sampling step으로도 고품질 이미지를 생성하고 텍스트 이해력과 이미지 디테일을 향상시켰다.

그 결과 8억 파라미터 규모 모델로 공개 diffusion model 중 최고 성능을 보였으며, 일부 평가는 폐쇄형 모델(DALL-E 3 등)을도 능가하는 수준에 이르렀다 .

Goal

Rectified Flow의 이론적 장점을 현실의 고해상도 텍스트-이미지 생성에 접목하여, 적은 추론 단계로도 고품질 이미지를 생성하고 diffusion model의 한계를 극복하는 것이다.

나아가 대규모 모델 스케일 업을 통해 개방형 모델로서 최고 수준의 성능에 도달하는 것을 목표로 한다 .

Motivation

기존 diffusion model은 뛰어난 이미지 생성능력을 보였지만 다수의 확률적 step을 거쳐야 하는 느린 sampling이 단점이고, 이를 개선하려는 다양한 시도가 있었다.

Rectified Flow는 직선 경로를 이용함으로써 이론적으로 sampling 효율을 높일 수 있으나, 아직 대규모에서 그 잠재력이 입증되지 않았다.

또한, 텍스트-투-이미지 모델의 Cross-Attention 방식은 텍스트 정보를 일방향으로만 활용하여 세부 이해력이나 텍스트 이미지 합성 능력(예: 글자 생성)에 한계가 있었다. 따라서 sampling 효율과 텍스트 표현력을 동시에 개선하고자 본 연구가 기획되었다.

Contributions

본 논문의 핵심 기여는 다음 세 가지로 요약된다 :

1. 대규모 확산 vs. 흐름 모델 비교 연구: 다양한 확산 및 Rectified Flow forward 과정의 조합들을 대규모로 실험하여 최적 설정을 규명하였다. 이를 위해 새로운 noise sampling 기법들을 Rectified Flow 훈련에 도입하여 기존 기법 대비 성능을 향상시켰다 .
2. 새로운 멀티모달 Transformer 아키텍처 - MM-DiT: 텍스트와 이미지 두 가지 token 스트림 각각에 전용 가중치를 부여하고, Transformer 내에서 양방향 정보 교환이 가능하도록 한 대규모 텍스트-투-이미지 Transformer를 제안
3. 스케일링 분석: 제안한 모델을 최대 8억 파라미터까지 스케일 업하여 검증 loss의 예측가능한 감소 경향을 보이고, 검증 loss 감소가 자동 및 인간 평가 지표상의 향상으로 강하게 연결됨을 보였다. 가장 큰 모델의 경우 SDXL(Open), DALL-E3(Closed) 등 최신 모델들을 정량지표와 사용자 선호도 면에서 능가하는 결과를 달성하였다.

Simulation-Free Flow Training

확률적 경로 시뮬레이션에 의존하지 않는 흐름 생성 모델을 학습하기 위해, 저자들은 Flow Matching 이론을 바탕으로 조건부 흐름 정합 loss(Conditional Flow Matching, CFM)을 유도한다. 우선 모델은 noise 분포 $p_1(\mathbf{x})$에서 데이터 분포 $p_0(\mathbf{x})$로의 매핑을 시간 지속적인 미분방정식(ODE)으로 정의한다. ODE의 형식은 다음과 같다:

\[dy_t = v_\theta(y_t, t)\,dt \tag{1}\]

• $t$: 연속 시간 변수 ($0 \le t \le 1$; $t=0$은 데이터 분포, $t=1$은 noise 분포를 의미)
• $v_{\theta}$: 시간 $t$에서 위치에 대한 속도 벡터 필드, 신경망 파라미터 $\theta$로 구현

기본적인 Continuous Normalizing Flow(CNF) 접근은:

• $t=1$에서$ y_1 \sim p_1$에서 시작해서,
• ODE를 수치적으로 쭉 적분해서 $t=0$에서 $y_0$를 얻는 방식이다.

문제는, CNF를 그대로 학습하려면:

• ODE solver를 학습 중에도 계속 돌려야 하고,
• 그 solver를 통해 backprop(미분)까지 해야 해서 대형 모델에는 너무 무겁다

대신 본 논문에서는 보다 효율적으로 벡터장 $v_{\theta}$ 자체를 회귀 학습하는 접근을 택한다. (Flow matching)

이를 위해 우선 forward 방향의 확률 경로 $p_t(\mathbf{x})$를 설정하는데, 데이터($p_0$)에서 noise($p_1$)로의 확률 분포의 연속적인 변화로 정의된다.

Forward 과정의 한 예로, Rectified Flow에서는 다음과 같은 직선 보간 경로를 사용한다:

\[z_t = a_t x_0 + b_t \epsilon \quad \text{where}\; \epsilon \sim \mathcal{N}(0, I)\]

• $a_0=1$, $b_0=0$이면 $t=0$에서 $z_0$ = $x_0$ (데이터).
• $a_1=0$, $b_1=1$이면 $t=1$에서 $z_1 = \epsilon$ (noise).
• 즉, $t$가 $ 0→1$로 가며 데이터에서 noise로 “연결”

\[p_t(z_t) = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)}[ p_t(z_t | \epsilon) ]\]

즉, 조건부 분포 $p_t(· | \epsilon)$를 $\epsilon$에 대해 평균 내서 주변화하면, 우리가 원하는 중간 시점의 분포 $p_t$를 얻는다.

위와 같이 forward 경로를 정의하면 $t=0$에서는 $\mathbf{x}(0)$ 그대로, $t=1$에서는 $\mathbf{z}$로 도달하게 되어 $p_t$가 양 끝단에서 $p_0$, $p_1$과 일치한다.

이제 이러한 경로에 대응하는 이론적 속도 필드 $u_t$를 정의한다.

\[ψ_t(\cdot|\epsilon) = a_t x_0 + b_t \epsilon\\ u_t(z|\epsilon) := ψ^′_t(ψ^{-1}_t(z|\epsilon) | \epsilon)\]

우리가 원하는 건 “주변 분포 $p_t(·)$를 생성하는 벡터장”임

조건부($\epsilon$이 고정된) 경로는 $ψ_t$로 명확히 정의되어 있고, 그때의 속도는 시간 미분 $ψ^′_t$로 표현된다.

이를 $z$ 좌표계에서 쓰려면 $x_0$ 대신 $z$를 넣어야 하므로, $x_0 = ψ_t^{-1}(z|\epsilon)$를 대입해 $u_t(z|\epsilon)$로 변환

이렇게 정의된 $u_t(z|\epsilon)$는 “조건부 확률 경로 $p_t(·|\epsilon)$”를 정확히 생성하는 벡터장이다.

이후에 주변 벡터장 $u_t(z)$를 얻기 위해 $\epsilon$에 대해 적절히 평균을 내는 식(논문에는 식 (6)로 이어짐)을 사용.

그 $u_t(z)$가 실제로 우리가 학습하고 싶은 대상이며, 이를 신경망 $v_\theta(z, t)$로 근사

조건부 벡터장 $u_t(z|\epsilon)$를 사용하여, 경로 $p_t$를 생성하는 벡터장 $u_t$를 구성할 수 있다.

\[u_t(z) = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)}\big[ u_t(z|ε) · \frac {p_t(z|\epsilon)}{p_t(z)} \big] \tag{6}\]

$z_t$는 사실 “랜덤한 $\epsilon$를 뽑고, 그 $\epsilon$에 맞는 ODE $z′=u_t(·|\epsilon)$를 따라감”의 혼합

즉, $p_t(z)$는 “여러 조건부 경로들의 혼합”

혼합 분포의 시간 변화는 각 구성요소의 시간 변화의 가중 합으로 표현된다.

이때 가중치는 “그 시점 $t$에서, 점 $z$가 $\epsilon$-조건부 구성요소에서 나왔을 확률” 즉 $ \frac {p_t(z|\epsilon)}{p_t(z)}$이다.

따라서 $z$에서의 평균 속도(=주변 벡터장)는 “각 조건부 속도 $u_t(z|\epsilon)$를, 그 조건부가 $z$에 기여하는 비율만큼 가중해 평균”한 값이어야 주변 분포 $p_t$가 올바르게 변한다.

베이즈 정리 $p(\epsilon|z,t) = \frac{p_t(z|\epsilon)p(\epsilon)}{p_t(z)}$를 쓰면 \(\begin{align} u_t(z) &= ∫ u_t(z|\epsilon) p(\epsilon|z,t) d\epsilon \notag \\ &= ∫ u_t(z|\epsilon) \frac{p_t(z|\epsilon) p(\epsilon)} {p_t(z)} d\epsilon \notag \\ &= E_{\epsilon \sim \mathcal{N}(0,I)}\big[ u_t(z|ε) · \frac {p_t(z|\epsilon)}{p_t(z)}].\notag \end{align}\)

Flow Matching loss은 모델의 예측 $v_{\theta}$가 이 이상적 속도 $u_t$와 일치하도록 만드는 것으로, 수식으로 표현하면 다음과 같다:

\[\mathcal{L}_{\text{FM}} = \mathbb{E}_{t, p_t(z)}\|v_{\theta}(z, t)-u_t(z|\epsilon)\|^2_2 \tag{7}\]

하지만 식 (7)의 $u_t$는 각 시점의 전체 분포에 대한 정보를 필요로 하므로 직접 계산이 불가능하다.

이를 해결하기 위해 Conditional Flow Matching 기법을 도입한다.

아이디어는 다음과 같다:

• 초기 데이터 샘플 $\mathbf{x}(0)$과 최종 noise 샘플 $\mathbf{z}$를 먼저 sampling
• 이를 조건으로 중간 시점 $t$의 표본 $\mathbf{x}(t)$를 생성
• $u_t$ 대신 쉽게 계산되는 조건부 목표 속도 $u(\mathbf{x}(0), \mathbf{z}, t)$를 얻을 수 있다. 이에 대한 loss은 다음과 같이 쓸 수 있다:

\[\mathcal{L}_{\text{CFM}} = \mathbb{E}_{t,p_t(z|\epsilon),p(\epsilon)}\|v_{\theta}(z, t)-u(z,\epsilon)\|^2_2 \tag{8}\]

FM → CFM

\[\begin{align} \mathcal{L}_{FM}(Θ) &= \mathbb{E}_{t,p_t(z)}||v_Θ(z, t) − u_t(z)||^2_2 \tag{30} \\ &= \mathbb{E}_{t,p_t(z)}||v_Θ(z, t)||^2_2 − 2 \mathbb{E}_{t,p_t(z)}⟨v_Θ(z, t) | u_t(z)⟩ + c \tag{31} \\ &= \mathbb{E}_{t,p_t(z)}||v_Θ(z, t)||^2_2 − 2 \mathbb{E}_{t,p_t(z|ϵ),p(ϵ)}⟨v_Θ(z, t) | u_t(z|ϵ)⟩ + c \tag{32}\\ &= \mathbb{E}_{t,p_t(z|ϵ),p(ϵ)}||v_Θ(z, t) − u_t(z|ϵ)||^2_2 + c^′ \tag{33} \\ &= \mathcal{L}_{CFM}(Θ) + c^′ \tag{} \end{align}\]

• (30) → (31) : 제곱 전개, $||u_t(z)||^2_2$은 파라미터 $\theta$와 무관하므로 상수 취급

• (31) → (32) :

  • 기댓값을 적분 형태로

    \[\mathbb{E}_{t,p_t(z|ϵ),p(ϵ)}⟨v_Θ(z, t) | u_t(z|ϵ)⟩ = ∬p_t(z∣ϵ)p(ϵ)⟨v_Θ(z,t)∣u_t(z∣ϵ)⟩dϵdz\]

  • $\frac{p_t(z)}{p_t(z)}$ 곱하기

    \[= ∫p_t(z)⟨v_Θ(z,t)∣∫\frac{p_t(z∣ϵ)}{p_t(z)}p(ϵ)u_t(z∣ϵ)dϵ⟩dz\]

  • (6)에 따라 $u_t(z) = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)}\big[ u_t(z|ε) · \frac {p_t(z|\epsilon)}{p_t(z)} \big] = \int u_t(z|\epsilon)\frac {p_t(z|\epsilon)p(\epsilon)}{p_t(z)}d\epsilon$ 대입

    \[= ∫p_t(z)⟨v_Θ(z,t)∣u_t(z)⟩dz =\mathbb{E}_{t,p_t(z)}⟨v_Θ(z, t) | u_t(z)⟩\]

  • 즉

    \[\mathbb{E}_{t,p_t(z)}⟨v_Θ(z, t) | u_t(z)⟩ = \mathbb{E}_{t,p_t(z|ϵ),p(ϵ)}⟨v_Θ(z, t) | u_t(z|ϵ)⟩\]

    이므로 (31) → (32)

이 과정은 “우리가 알 수 없는 전체 데이터 분포의 벡터장($u_t(z)$)을 직접 학습하는 것”과 “우리가 생성한 데이터-noise 경로($u_t(z|\epsilon)$)를 학습하는 것”이 최적화 관점에서 동일하다는 것을 보여준다.

이제 $z_t = a_tx_0 + b_t \epsilon$ 에서 $x_0 = \frac{z_t - b_t\epsilon}{a_t}$ 를 얻는다. 또한 $z_t$를 미분하면 $\frac{d}{dt}z_t = a^′_t x_0 + b^′_t \epsilon$ 이다.

동시에 CFM 에서는 $\frac{d}{dt}z_t = u_t(z_t \mid \epsilon)$이므로

\[\begin{align} u_t(z_t \| \epsilon) &= a^′_t x_0 + b^′_t \epsilon \notag \\ &= a^′_t \frac{z_t - b_t\epsilon}{a_t} + b^′_t \notag \\ &= \frac{a_t’}{a_t} z_t - \epsilon b_t\left(\frac{a^′_t}{a_t} - \frac{b^′_t}{b_t}\right)\tag{9} \end{align}\]

SNR(signal-to-noise ratio) $\lambda_t := \log \frac{a_t^2}{b_t^2}$ 를 미분하면 $\lambda_t’ = 2\left(\frac{a_t’}{a_t} - \frac{b_t’}{b_t}\right)$ 이고 이를 대입하면

\[u_t(z_t \mid \epsilon) = \frac{a_t’}{a_t} z_t - \frac{b_t}{2}\,\lambda_t’ \epsilon \tag{10}\]

를 얻는다. 이를 다시 CFM loss함수 (8)에 넣으면

\[\begin{align} \mathcal{L}_{\text{CFM}} &= \mathbb{E}_{t,p_t(z|\epsilon),p(\epsilon)}\|v_{\theta}(z, t)-u(z,\epsilon)\|^2_2 \tag{8} \\ &= \mathbb{E}_{t,p_t(z\mid\epsilon),p(\epsilon)}\Big\| v_\theta(z_t,t) -\frac{a_t’}{a_t} z_t + \frac{b_t}{2}\lambda_t’ \epsilon \Big\|^2_2 \tag{11} \end{align}\]

여기서 noise 예측 모델 $\epsilon_\theta$를 $\frac{-2}{\lambda_t’ b_t} \Big(v_\theta(z_t, t) - \frac{a_t’}{a_t} z_t\Big)$ 로 정의하면,

\[\mathcal{L}_{\text{CFM}} = \mathbb{E}_{t,p_t(z\mid\epsilon),p(\epsilon)} \Big( -\frac{b_t}{2}\lambda_t’ \Big)^2 \big\|\epsilon_\theta(z_t,t) - \epsilon\big\|^2 \tag{12}\]

가 된다.

모양이 Diffusion 모델에서 보던 noise 예측 MSE와 매우 유사한 것을 볼 수 있다.

즉 이 식을 다시 쓰면

\[\mathcal{L}_w(x_0) = -\frac{1}{2}\mathbb{E}_{t \sim \mathcal{U}(t),\epsilon \sim \mathcal{N}(0, I)}\big[w_t\,\lambda_t’ \Vert \epsilon_\theta(z_t,t) - \epsilon \Vert^2\big]\]

가 된다. (CFM에서는 $w_t = -\frac{1}{2}\lambda_t’ b_t^2$)

$w_t$, 즉 timestep $t$에 따른 가중치를 변경하더라도 최적화 해는 동일하다.

이 말은 즉,

SD3 입장에서,

Flow Matching / Rectified Flow / Diffusion을 전부 “noise 예측 MSE” 하나의 공통 언어로 다뤄서, 어떤 선택이 성능/안정성/샘플링 효율에 좋은지 비교·튜닝할 수 있게 된다.

이 모든 학습 과정에서 ODE 시뮬레이션을 돌릴 필요가 없다는 점이 바로 “Simulation-Free Training”이라는 이름의 핵심이다.

1. $x_0 \sim p_0, \epsilon \sim \mathcal{N}(0,I), t \sim \text{some distribution}$ 에서 샘플링
2. $z_t = a_t x_0 + b_t \epsilon$를 한 번에 계산
3. analytic하게 정의된 $u_t(z_t\mid\epsilon) $(그리고 그로부터 noise 타겟 $\epsilon$)을 써서
4. 단순 MSE loss로 네트워크를 학습한다.

즉, 학습 단계에서는 “forward SDE/ODE 시뮬레이션”이 전혀 필요 없다.

이 점이 기존 diffusion(CNFs를 시뮬레이션하거나, SDE를 샘플링해야 했던 방식)과의 가장 큰 차이이고, SD3가 거대한 Rectified Flow Transformer를 현실적으로 학습할 수 있게 해주는 수학적 기반이다.

정리하면, 이 섹션에서는

1. 생성 모델을 ODE(velocity field)로 보는 관점에서 출발해서,
2. Flow Matching / Conditional Flow Matching 이론을 가져와
3. Gaussian path $z_t = a_t x_0 + b_t \epsilon$위에서 conditional vector field $u_t(z_t \mid \epsilon) $를 analytic하게 구하고,
4. 이걸 SNR 기반 noise 예측 loss로 재파라미터라이즈해서,
5. Diffusion / Rectified Flow / 기타 flow 모델 objective를 하나의 $\mathcal{L}_w$ 형태로 통일한다.

이를 기반으로 뒤에 나오는

• Flow trajectories : 어떤 $a_t$, $b_t$를 사용하여 어떤 경로를 따라갈것인가
• SNR Sampler : 어떻게 $t$를 샘플링할것인가

를 선택하여 비교한다.

Flow Trajectory

이제 “데이터 $x_0$에 가우시안 noise $\epsilon$를 어떻게 섞어가며 $z_t = a_t x_0 + b_t \epsilon$로 움직일 것인가” 를 정하는 probability path / noise schedule의 서로 다른 선택지를 설명한다.

저자들은 이 모델들이 본질적으로 “데이터($x_0$)와 노이즈($\epsilon$)를 잇는 경로(Trajectory)”와 “학습 시 시간별 가중치($w_t$)”를 어떻게 설정하느냐의 차이일 뿐임을 보여준다

---

1. Rectified Flow (RF)

이 논문이 주력으로 삼고 있는 모델이며, 가장 단순하고 직관적인 경로를 사용한다.

\[z_t = (1 - t)x_0 + t\epsilon,\quad t\in[0,1]\]

이때 가중치는 $w_t= \frac{t}{t-1}$ 를 사용한다.

2. EDM (Elucidated Diffusion Models)

최근 고해상도 이미지 생성에서 매우 강력한 성능을 보여주어 사실상의 표준(de-facto) 중 하나로 자리 잡은 방식이다.

\[z_t = x_0 + b_t\epsilon\]

데이터에 노이즈를 더하는 방식이지만, 노이즈의 크기($b_t$)가 특정 분포를 따르도록 설정한다.

특징:

• Log-Normal 분포: 노이즈 레벨($\sigma$)이 로그 정규 분포를 따른다고 가정하고 스케줄링한다.
• SNR($\lambda_t$) 역시 정규 분포 형태를 띈다.
• 가중치 ($w_t$): 중간 정도의 노이즈 레벨(이미지의 구조가 형성되는 구간)에 집중하도록 설계된 복잡한 가중치 함수를 사용

3. Cosine (Improved DDPM Cosine Schedule)

초기 디퓨전 모델들(DDPM 개량형)에서 많이 쓰인 방식

\[z_t = \cos(\frac{\pi}{2}t)x_0 + \sin(\frac{\pi}{2}t)\epsilon\]

특징:

• $\epsilon$-parameterization (noise 예측) : $w_t = \text{sech}(\lambda_t/2)$
• $v$-prediction (벡터장 예측) : $w_t = e^{-\lambda_t/2}$

4. (LDM-)Linear

DDPM 계열의 linear $β$ schedule과, 그것을 살짝 수정한 LDM의 linear schedule을 말하며 실험의 baseline으로 사용된다.

• DDPM:

  • timestep $t = 1\ldots T$에 대해

    $\beta_t$를 $\beta_\text{min} \to \beta_\text{max}$로 선형 증가

    예: $\beta_\text{start} = 0.0001,\,\beta_\text{end} = 0.02 (1000 step)$ 같은 설정.

  • 누적 계수 $\alpha_t = 1-\beta_t, \bar\alpha_t = \prod_{s\le t}\alpha_s$

  • $z_t = \sqrt{\bar\alpha_t} x_0 + \sqrt{1-\bar\alpha_t}\,\epsilon$

---

SD3는 이 네 가지를 전부 CFM 통일식 $z_t = a_t x_0 + b_t\epsilon$ 과 가중치 $w_t$안에 넣은 다음, 대규모 실험으로 “어떤 path + 가중치 선택이 가장 좋은가”를 비교한다.

Tailored SNR Samplers for RF models

Rectified Flow 모델을 효율적으로 학습하려면 어느 시점의 데이터에 더 중점을 둘지 결정하는 것이 중요하다.

기본적으로 CFM loss은 $t\sim \text{Uniform}(0,1)$으로 모든 timestep을 균등하게 학습한다.

그러나 저자들은 중간 시점의 예측이 특히 어렵다는 점에 주목했다.

• $t$가 0에 가까우면 모델은 거의 데이터(신호)만 보고 예측
• $ t$가 1에 가까우면 거의 noise만 보고 예측
• 중간 $t\approx0.5$에서는 신호와 잡음이 섞여 최적 예측이 애매

따라서 중간 시간대의 학습 비중을 높이는 것이 모델 성능을 높일 열쇠라고 보았다.

$t\sim \mathcal{U}(t)$ 대신 density $\pi(t)$가 도입되면, RF 모델의 가중치는 $w_t^\pi = \frac{t}{1-t}\pi(t)$가 된다.

여기서 $\pi(t)$로 사용될 timestep density function 3가지를 설명한다.

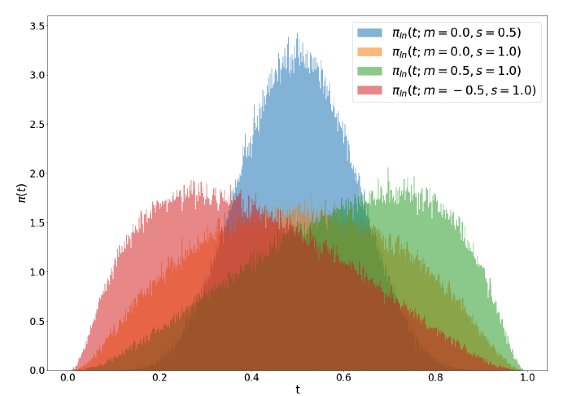
• Logit-Normal Sampling

  • timestep $ t$를 정규분포 $\rightarrow$ Logit 함수를 통해 샘플링한다.

    

    • $\text{logit}(t) = \ln\frac{t}{1-t}$가 정규분포 $\mathcal{N}(m,s^2)$를 따르도록 하는 분포
    \[\pi_{\ln}(t;m,s) = \frac{1}{t(1-t)s\sqrt{2\pi}} \exp\Big(-\frac{(\text{logit}(t)- m)^2}{2s^2}\Big), \qquad t\in(0,1)\tag{19}\]

  • $m$ : location 파라미터

    • 양수이면 분포가 noise 쪽($t\to1$)으로 치우치고
    • 음수이면 데이터 쪽($t\to0$)으로 치우친다.

  • $s$ : 척도(scale) 파라미터

    • 값이 클수록 분포가 평평해져 넓은 영역을 커버

  • 말이 어렵지, 코드로 보면 쉽다

    u ~ Normal(m, s^2)          # 실수축에서 정규분포 샘플
    t = sigmoid(u) = 1 / (1 + exp(-u))  # 이를 (0,1)로 투영
    

• Mode Sampling (Heavy Tails)

  • Logit-normal은 양 끝에서 밀도가 0이어서 학습이 부족해질 가능성이 있어 저자들이 제안한 방법

    \[t = f_\text{mode}(u;s) = 1-u-s\cdot(\cos^2(\frac{\pi}{2}u)-1+u) \tag{20}\]
    • 이때 $s$를 $-1 \le s \le \frac{2}{\pi-2}$로 제한하여 $f^{-1}$을 정의한다.

  • density $\pi_\text{mode}(t;s) = \frac{d}{dt}f^{-1}_\text{mode}(t)$가 된다.

  • $s$에 따른 sampling distribution 모양

    

    • $s > 0$ : 분포가 중간 ($t=0.5$ 주변) 쯤을 자주 sampling
    • $s < 0$ : 분포가 양 끝 ($t=0, t=1$) 쯤을 자주 sampling
    • $s = 0$ : Uniform distribution

• Cosine Mapping (CosMap)

  • 코사인 스케줄을 Rectified Flow timestep $ t$에 mapping하기 위한 방법

  • Uniform 분포 $u$에 대해 cosine 스케줄 $2\log\frac{\cos(\frac{\pi}{2}u)}{\sin(\frac{\pi}{2}u)} = 2 \log \frac{1-f(u)}{f(u)}$을 $f$로 다시 풀면

    \[t = f(u) = 1-\frac{1}{\tan(\frac{\pi}{2}u)+1}\]

  • 즉, 다음과 같은 $\pi(t)$를 얻을 수 있다.

    \[\pi_\text{CosMap}(t) = \Big|\frac{d}{dt}f^{-1}(t)\big| = \frac{2}{\pi-2\pi t + 2\pi t^2}\]

이상 세 가지 분포로 Rectified Flow 모델을 학습하면, 기존 균등 sampling 대비 성능이 향상됨을 저자들은 확인하였다. 요약하면 “중간 위주로 골고루 학습시키되, 극단도 조금은 보강”하는 전략으로, 이러한 noise 스케줄링 기법이 본 논문의 핵심 기법 중 하나이다.

Multimodal Transformer Architecture (MM-DiT)

기존 Stable Diffusion 계열 모델에서는 CLIP 등으로부터 얻은 텍스트 embedding을 이미지 생성 UNet에 주입(cross-attention 등)하는 방식이었다.

저자들은 이러한 단방향 조건 주입이 텍스트와 이미지 간 상호작용의 부족을 초래한다고 보고, Transformer 기반의 새로운 백본을 제안했다.

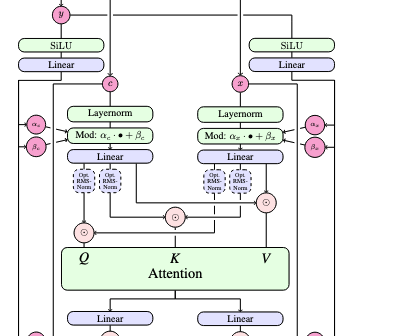
이 아키텍처는 DiT (Diffusion Transformer) 구조 를 기반으로 하되, 이미지 token 스트림과 text token 스트림을 모두 Transformer 내부에서 처리한다

(a) 텍스트와 이미지를 입력으로 받아 각각 **별도의 인코딩 경로를 거친 후, **patch 단위의 이미지 latent와 text token 시퀀스를 하나로 연결하여 Transformer 인코더에 투입

(b) MM-DiT 블록 내부에서는 텍스트 전용 가중치와 이미지 전용 가중치를 사용하는 두 개의 병렬 모듈이 존재, attention 연산 시 텍스트+이미지 token 전체에 걸쳐 수행되므로 두 모달리티 간 양방향 정보 교환이 가능하다

Encoding

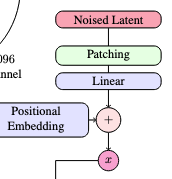
• Image :

  

  • 원본 이미지를 목표 해상도(예: 512, 1024)로 resize한한 뒤, VAE 인코더에 넣어 $z \in \mathbb{R}^{C \times H’ \times W’}$ latent로 변환

  • SD3에서는 채널 수 $C=16$, downsampling = $8$을 갖는 autoencoder 사용하여 $H’ = H/8, W’ = W/8$ 크기의 latent를 얻는다.
  • 이 latent에 대해 $ 2\times 2$ 패치 임베딩(Conv)으로 패치 토큰 시퀀스를 만들고, positional encoding을 더한 뒤 MM-DiT의 image stream 입력으로 사용

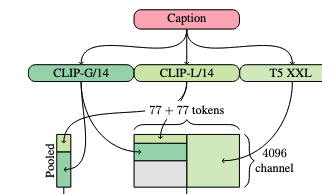
• Text :

  텍스트 프롬프트는 동결된 텍스트 인코더들(CLIP ViT-L/14, CLIP ViT-bigG/14, T5-XXL)을 통해 인코딩된다. 여기서

  

  1. 문장 전체를 풀링한 글로벌 임베딩 $c_\text{vec}$을 concat 후 선형 변환하여 하나의 조건 벡터로 생성

     • timestep 임베딩+CFG로 MM-DiT 블록에 삽입

     • 풀링된” 텍스트 벡터는 문장 세부(단어별, 구문별) 정보를 잃기 쉬움

  2. T5/CLIP에서 나온 token 단위 시퀀스 임베딩 $c_\text{ctxt}$을 그대로 text token stream으로 사용

     이 토큰 시퀀스에 1D positional encoding을 더해 MM-DiT의 text stream으로 넣고, 이미지 토큰과 동일한 Transformer 블록 안에서 양방향 어텐션을 수행

Transformer 백본으로서 MM-DiT는 기본적으로 DiT와 동일한 Transformer 블록 구조를 반복한 것이다.

그러나 가중치 공유 방식이 다르다:

본 모델에서는 텍스트 전용 가중치과 이미지 전용 가중치 두 가지로 분리하여 사용

각 Transformer 블록 내 모듈(LayerNorm, MLP 등)을 텍스트 입력에 대해서는 별도 파라미터 세트로, 이미지 입력에 대해서는 또 다른 세트로 동작시킨다.

이는 마치 두 개의 Transformer가 병렬로 존재하는 듯하지만, attention 연산만은 텍스트+이미지 token을 함께 연결하여 수행함으로써 두 모달리티 사이의 정보를 교환한다.

Image-Text : MM-DiT vs Cross Attention

• $X$ : Image embedding
• $T$ : Text embedding

Cross Attention

텍스트는 “참조용 사전”에 가까움

• Loss → 이미지 토큰 → Cross-Attn → 텍스트 토큰(고정)

  • $Q = X W_Q$ (이미지에서만 query)

  • $K = T W_K,\; V = T W_V$ (텍스트에서만 key/value)

$\text{Attn}(X, T) = \text{softmax}\Big(\frac{Q K^\top}{\sqrt{d}}\Big)V$

MM-DiT

이미지와 텍스트를 모두 Transformer 안에서 동일한 “시퀀스”로 취급 (텍스트 + 이미지 둘 다 업데이트)

• 토큰 concat + Self-Attention

  • 하나의 긴 시퀀스로 합친다:

    $Z = [T; X] \in \mathbb{R}^{(L_t + L_x) \times d}$

  • MM-DiT 블록의 Self attention

    $Q = ZW_Q,\quad K = ZW_K,\quad V = ZW_V$

    $\text{Attn}(Z) = \text{softmax}\Big(\frac{QK^\top}{\sqrt{d}}\Big)V$

Task별 차이

1. 타이포그래피 / 글자 생성
2. 복잡한 장면 텍스트 이해 / 수식적 관계

• MM-DiT는 Transformer만으로 끝까지 밀어붙이는 구조
  • 대규모 학습에 유리하고,
  • 멀티모달 토큰 구조를 확장(비디오, 오디오 등) 용이
• 대신 메모리/연산량 $\uparrow$

Experiments

Improving Rectified Flows

첫 번째 실험은 앞서 정의한 여러 가지 확산/흐름 공식들의 성능을 비교하여, Rectified Flow를 대규모에서 활용할 최적의 설정을 찾는 것이다.

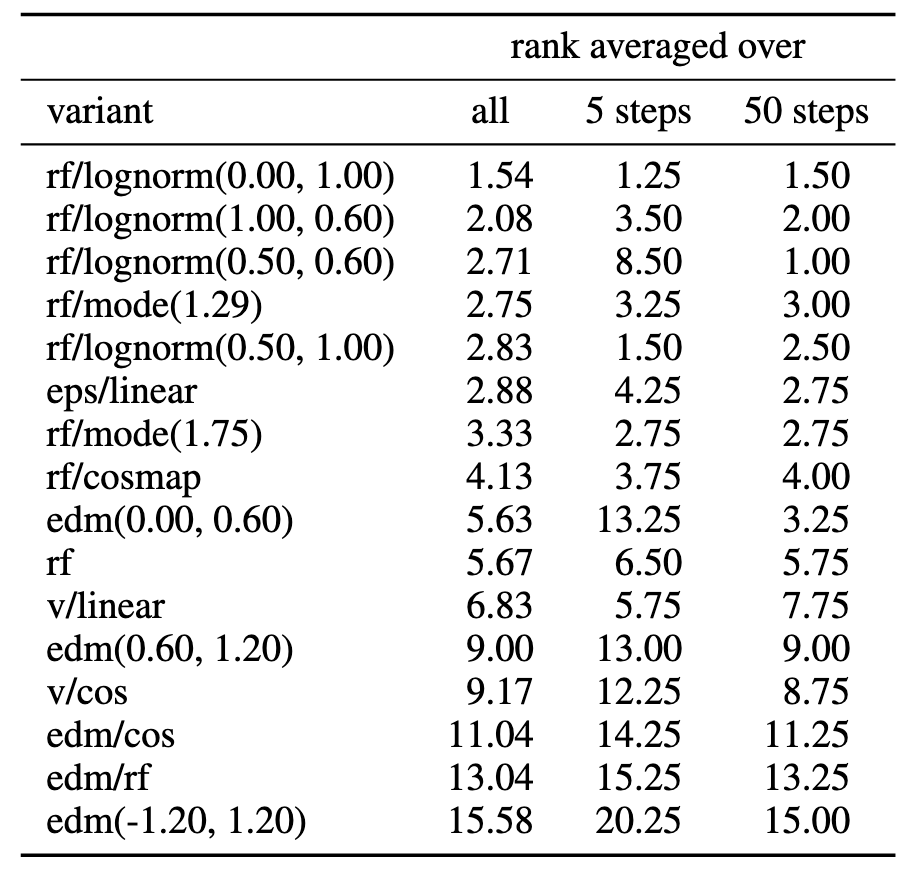
저자들은 ImageNet 및 CC12M 데이터셋에서 총 61종의 모델 변형을 동일한 조건 하에 학습시켰다.

비교 대상에는

• 기존 diffusion model 스케줄
  • $\epsilon$-prediction vs $\mathbf{v}$-prediction
  • Linear schedule (eps/linear, v/linear) vs Cosine schedule (eps/cos, v/cos)
• Rectified Flow + 다양한 sampler
  • RF, LogitNormal RF rf/lognorm(m,s), Mode RF rf/mode(s) , CosMap RF rf/cosmap
• EDM
  • 기본 edm(Pm,Ps), RF log-SNR 가중치의 edm/rf, v/cos 스케줄을 공유하는 edm/cos

모든 모델은 동일한 아키텍처와 optimizer로 학습되며, 24가지 다양한 sampling 조건에서 CLIP Score와 FID를 평가하여 Pareto 우수성 기준의 종합 랭킹을 산출한다.

24가지 세팅에서의 등수를 평균

• EMA 유 or 무
• 데이터셋 ImageNet or CC12M
• 6가지 sampler
  • 50 step - CFG scale 1.0, 2.5, 5.0
  • 5, 10, 25 step - CFG scale 5.0

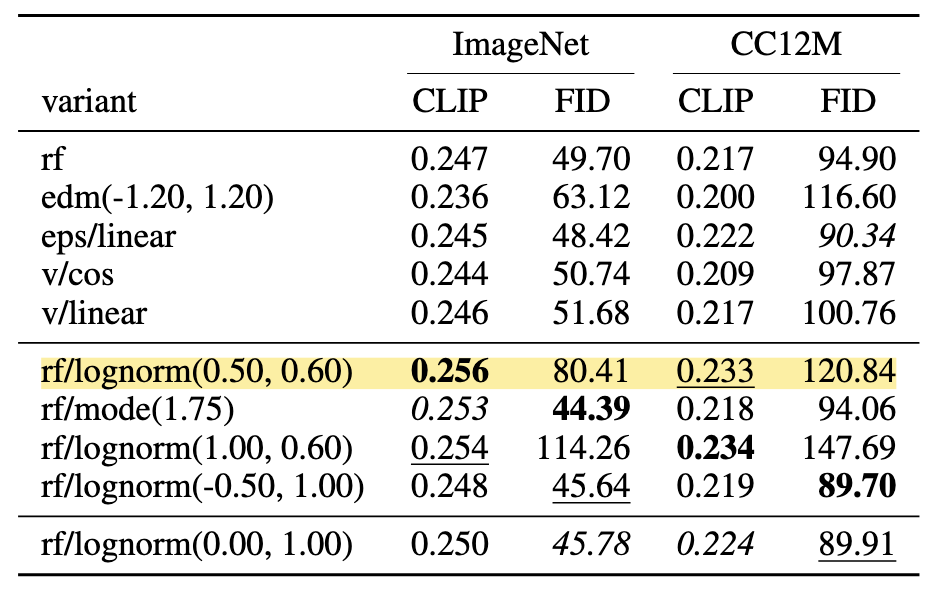
상위권에는 Rectified Flow 기반 변형(특히 logit-normal 분포 사용)이 위치했으며, 기존 LDM-Linear(eps/linear) 등 확산 기반은 그보다 낮았다.

위 표에서 알 수 있듯이, Rectified Flow + Logit-Normal($μ=0$,$σ=1$) 조합이 가장 안정적으로 상위 성능을 보였다.

이는 균일 sampling RF(rf)보다 우수하여 중간 timestep에 가중을 둔 효과를 입증하며, 기존 확산(LDM 선형)보다도 일관된 성능 개선을 달성했음을 의미한다.

또한 일부 조합은 특정 조건에서만 좋고 다른 조건에서는 불안정한 경향이 있었다.

예: rf/lognorm(0.50,0.60)은 50 step에서 1위지만 5 step에선 순위 하락

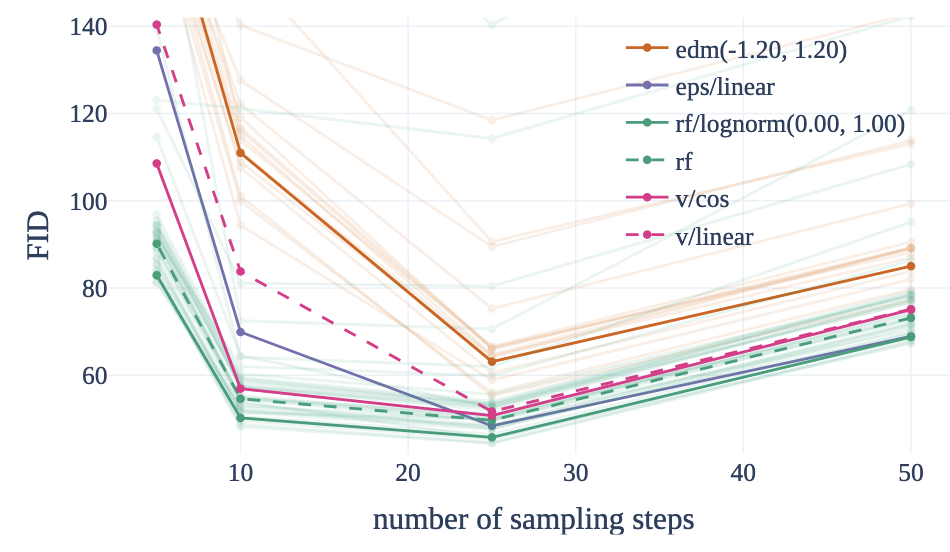
그림의 결과처럼, Rectified Flow 계열은 적은 step으로 생성할 때 다른 공식보다 높은 품질을 유지하며, 25 step 이상 충분한 step에서는 최적 조합(rf/lognorm)이 기존 확산(eps/linear)과 대등한 수준까지 올라섰다 .

요약하면, 이 대규모 비교 실험을 통해 Rectified Flow를 적용한 새로운 공식이 기존 diffusion model을 능가할 수 있음을 보였다.

특히 noise 분포 재가중 전략이 주효하여, RF의 이론적 강점(빠른 sampling)을 실제 성능 향상으로 연결시켰다.

이러한 최적 공식을 바탕으로 이후 실험들은 모델 아키텍처와 데이터 측면의 개선으로 집중된다.

Improving Modality Specific Representations

텍스트-이미지 모델의 구성 요소들을 향상시켜 최종 성능을 끌어올린린다.

세 가지 측면에서 개선이 이루어졌는데

1. Autoencoder
2. Caption
3. T2I Backbone

각 개선의 효과를 개별적으로 분석한 결과는 다음과 같다.

Autoencoder Latent dimensions

Stable Diffusion은 이미지 RGB를 낮은 차원의 latent로 압축하여 효율을 높이는데, 이 latent 차원 수가 reconstruction 한계로 작용한다.

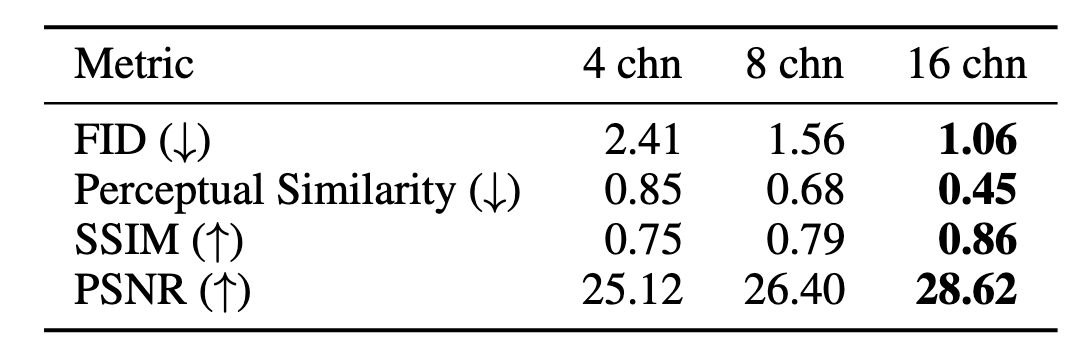
저자들은 채널 수를 $4→8→16$으로 늘려가며 AutoEncoder의 reconstruction 성능을 측정했다.

그 결과 채널이 증가할수록 FID 개선 및 지각적 유사도 향상이 나타났다.

예: 4채널 FID=2.41 → 16채널 FID=1.06)

채널 수가 높으면 latent representation의 복잡도가 올라가 생성이 어려워지지만, 그만큼 모델 용량을 키우면 품질이 향상됨을 확인한 것

실제로 16채널 설정에서 FID 스케일링 곡선이 가장 가파르게 개선되었고, 채널 증가 효과는 모델 크기가 커질수록 더욱 뚜렷했다.

따라서 이후 실험에서는 16채널 VAE를 채택하여 최대 성능을 추구했다.

Caption

대규모 이미지-텍스트 학습에서 종종 인간 작성 캡션이 단순하여 모델 성능을 제한한다는 보고가 있다.

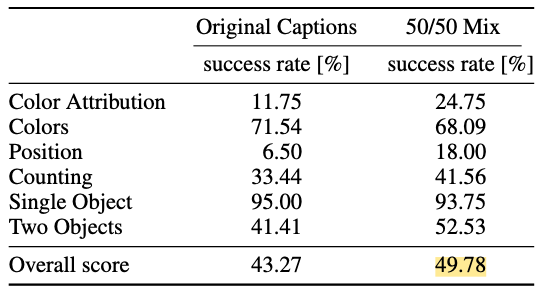
이를 극복하고자, 저자들은 최신 Vision-Language 모델(CogVLM)을 사용해 이미지로부터 상세한 합성 캡션을 생성하고, 원본 캡션과 50:50 비율로 혼합하여 학습 데이터로 사용했다.

합성 캡션만 쓰면 VLM 지식 분포에 편향되어 일부 개념을 잊을 위험이 있음

합성 캡션은 배경, 구성, 숨겨진 요소 등을 더 풍부하게 묘사하여 데이터 다양성을 높인다.

25만 step 학습 후 GenEval benchmark로 비교한 결과, 합성 캡션을 포함한 모델이 전반적인 프롬프트 이해도 점수에서 크게 향상되었다

예: Overall 점수 43.27 → 49.78

특히 색상 위치 설명, 개수 representation 등 인간 캡션이 놓치기 쉬운 항목에서 성능이 2배 가까이 상승했다.

Text-to-Image Backbone

제안된 MM-DiT Transformer의 효과를 검증하기 위해, 동일 조건에서 기존 Diffusion 백본들과 비교한다.

비교 대상은

1. DiT (Vanilla) – 텍스트 시퀀스를 이미지 patch 시퀀스에 단순 연결하여 Transformer로 처리 (cross-attention 없음)
2. CrossDiT – DiT 구조이지만 각 블록에서 Cross-Attention으로 텍스트 처리를 분리한 변형
3. UViT – UNet과 ViT의 하이브리드 구조 (Stable Diffusion의 Improved U-Net 백본으로 볼 수 있음)
4. MM-DiT
   1. Two-stream : 텍스트/이미지 2세트 가중치
   2. Three-stream : CLIP의 텍스트와 T5 텍스트까지 3세트 가중치

Vanilla DiT는 UViT보다 최종 성능이 낮았고, CrossDiT는 UViT보다 수렴이 빠르고 성능도 향상되었다.

그러나 가장 두드러진 것은 MM-DiT로, 초기 수렴 속도와 최종 성능 모두에서 타 모델 대비 우월함을 보였다.

3세트 가중치 MM-DiT는 2세트 대비 약간의 성능 이득이 있었으나 매개변수와 메모리 비용 증가를 고려하면 미미한 수준이라 판단되어, 최종 모델에는 2세트 구조를 사용했다.

결국 양방향 모달 결합과 모달별 전용 파라미터화라는 설계가 텍스트-이미지 조합 생성에 효과적임이 입증되었다.

Training at Scale

VAE와 Text encoder는 frozen되어있기 때문에 모든 이미지 및 텍스트 embedding을 사전에 계산해놓는다.

Fine tuning on high resolution

이렇게 준비된 데이터로 저해상도 256×256으로 pre-train한다.

그런 다음, 더 높은 해상도 + 다양한 종횡비(aspect ratio)로 fine-tuning하는데, 이때 mixed precision 학습에서 gradient가 불안정해진다( loss 발산 )

mixed precision : 연산은 FP16으로, weight 표현은 FP32로 학습하는 방식

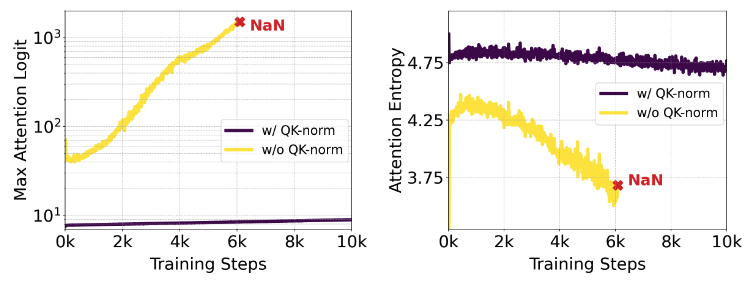
QK-Normalization

Dehghani et al. (2023)에서 분석한 바로는 ViT 학습할 때, Attention entropy가 점점 떨어지고, 혹은 어떤 헤드는 특정 위치에만 거의 확률 1로 쏠리는 식으로, Softmax가 매우 날카롭게(sharp) 된다.

이게 그냥 “모델이 확실해진다” 수준이면 괜찮은데, dot product $QK^\top$가 계속 커지다 보면 softmax의 입력(logit)이 너무 커져서 수치적으로 overflow/underflow, gradient 폭주로 이어진다.

저자들은 Dehghani et al. (2023) 에서 제안된 QK-Normalization을 사용한다.

QK-Normalization : Q, K 벡터의 scale을 제한

1. Q와 K에 정규화(norm) 적용
2. 그 결과를 가지고 dot-product

SD3에서는 RMSNorm으로 정규화

RMSNorm

LayerNorm과 비슷한데, 평균을 빼지 않고 RMS(root mean square)로만 스케일을 맞추는 정규화

벡터의 길이(에너지)를 일정하게 맞춤

MM-DiT 구조에서 Text/Image 스트림 둘 다 적용

• QK-normalization을 하지 않으면 attention logit의 분산/최댓값이 점점 커지는 패턴(불안정)
• QK-normalization을 넣으면 그게 상당히 눌려서 안정적인 분포를 유지

이 덕분에 bf16-mixed precision으로도 고해상도 훈련이 안정적으로 돌아간다

처음부터 QK-normalization을 쓰지 않고 프리트레인된 모델이라도, 나중에 고해상도 파인튜닝 단계에서 QK-normalization 레이어를 끼워 넣어도 모델이 금방 적응하고 학습이 안정된다고 한다.

Positional Encoding for Varying Aspect Ratios

256×256에서 학습해둔 2D Fourier positional encoding을, 고해상도 + 여러 종횡비(H×W)에서 좌표계 일관성을 유지하도록 “키우고 잘라 쓰는 방법”을 설명한다.

2D positional frequency embedding은 grid(H×W)크기가 달라지면 position 정보가 깨진다.

때문에 다양한 종횡비를 지원할 수가 없다.

때문에 SD3에서는 큰 공통 좌표 grid를 만들고, 거기서 centor crop을 하는 방식으로 원하는 H×W에 맞는 position encoding을 수행한다.

구체적으로는 목표 해상도를 $S^2$로 정한다. (예 : $1024 \times 1024$)

각 배치마다 $S^2$에 가까운 하나의 $H \times W$를 정하여 배치 내에서 padding을 필요없게 한다.

다양한 종횡비들 중 가로/세로 최대 길이를 $W_\text{max}$, $H_\text{max}$라 할 때, latent 크기는 $(\frac{H_\text{max}}{16}\times \frac{W_\text{max}}{16})$가 된다. ($h_\text{max} \times w_\text{max} $)

그런 다음,

1. 특정 배치의 $H \times W$가 있을때, latent 크기를 $h = H/16$, $w =W/16$이라고 하면
2. ($h_\text{max} \times w_\text{max} $)인 거대한 position grid에서 $h \times w$ 만큼 center crop한다.
3. $h \times w$ 에 Fourier embedding 적용하여 2D positional encoding을 수행한다.

Resolution-dependent shifting of timestep schedules

해상도가 커지면, 픽셀 수가 많아져서 더 많은 noise를 추가해야한다. 그래서 같은 $ t$에서도 고해상도 이미지 쪽이 아직 noise가 덜 추가된 상태이다.

그러니 고해상도에서는 $ t$를 더 앞으로(더 noise가 많은 쪽으로) 밀어줘야 한다.

해상도 $H \times W$이고 픽셀 수가 $n = H\cdot W$라고 할 때, 원본 이미지 $z_0$를 픽셀값이 $c$인 상수 이미지라고 가정하자. 이때,

$z_t = (1 - t)c\mathbb{1} + t\epsilon,\quad \mathbb{1}, \epsilon \in \mathbb{R}^n$

각 픽셀은 동일한 확률변수

$Y = (1 - t)c + t\eta,\quad \eta \sim \mathcal N(0,1)$

의 독립 샘플이라고 보면 된다.

즉 이미지 $z_t$는 $(z_t)_i = (1 - t)c + t\eta_i,\quad \eta_i \sim \mathcal N(0,1)$ 를 모아놓은것

이때:

• 기댓값: $\mathbb{E}[Y] = (1 - t)c$

• 분산, 표준편차: $\mathrm{Var}(Y) = t^2,\quad \sigma(Y) = t$

즉, $(z_t)_i$는 평균이 $(1-t)c$, 표준편차가 $ t$인 확률 분포에서 샘플링된 것이 된다.

우리는 $c$를 알고 싶고, 관측 가능한 것은 각 픽셀의 값 $z_{t,i}$ 뿐이라고 한다. 상수 이미지라는 사실은 알고 있으니까,

1. 위에서 $\mathbb{E}[Y] = (1 - t)c$ 이므로 $c = \frac{1}{1 - t}\mathbb{E}[Y]$
2. 실제 $\mathbb{E}[Y]$를 모르기 때문에, $z_t$에서 $n$개의 표본 픽셀을 관찰한다. : $\bar{z}t = \frac{1}{n}\sum^n{i=1} (z_t)_i$
3. 따라서 자연스러운 추정량은 $\hat{c} = \frac{1}{1 - t}\bar{Y} = \frac{1}{1 - t}\frac{1}{n}\sum_{i=1}^{n} (z_{t})_i$

이제 $\hat{c}$의 표준편차(=추정 오차의 크기) 를 계산한다.

• $\bar{Y}$의 분산은

$\mathrm{Var}(\bar{Y}) = \frac{\mathrm{Var}(Y)}{n} = \frac{t^2}{n}$

• 따라서 $\hat{c} = \frac{1}{1 - t}\bar{Y}$의 분산은

$\mathrm{Var}(\hat{c}) = \frac{1}{(1 - t)^2}\mathrm{Var}(\bar{Y}) = \frac{1}{(1 - t)^2}\frac{t^2}{n}$

• 표준편차는

$\sigma(t, n) = \sqrt{\mathrm{Var}(\hat{c})} = \frac{t}{1 - t}\sqrt{\frac{1}{n}}$

즉, $\sigma(t,n)$은 “우리가 상수 이미지라는 걸 알고 있을 때, $z_t$만 보고 원래 상수 값 $c$가 얼마나 불확실한지”를 나타낸다.

픽셀 수 $n$이 커질수록, $\sqrt{1/n}$ 때문에 불확실성이 줄어든다.

예: 가로세로를 둘 다 두 배로 늘리면 $n$이 4배 → $\sqrt{1/n}$이 1/2로 줄어든다.

→ “같은 $ t$에서 원래 $c$를 추정하는 오차가 절반으로 줄어든다.”

직관적으로, 픽셀이 많으면 평균을 더 잘 낼 수 있으니까, 똑같이 노이즈를 섞어도 고해상도 이미지는 아직 더 “정보를 많이 유지하고 있다”는 뜻이다.

이제 해상도 $n$에서의 어떤 timestep $t_n$이 주는 불확실성과 해상도 $m$에서의 어떤 timestep $t_m$이 주는 불확실성이 같게 맞춰야 한다. $\sigma(t_n, n) = \sigma(t_m, m)$ $\rightarrow$ $\frac{t_n}{1 - t_n}\sqrt{\frac{1}{n}} = \frac{t_m}{1 - t_m}\sqrt{\frac{1}{m}}$

그래야 다양한 해상도에 상관없이 Noise 비율이 일정한 알맞는 timestep $ t$를 찾을 수 있으니까

$\frac{t_n}{1 - t_n}\sqrt{\frac{1}{n}} = \frac{t_m}{1 - t_m}\sqrt{\frac{1}{m}}$ 에서 양변에 $\sqrt{n}\sqrt{m}$을 곱하면 $t_n \sqrt{m},(1 - t_m) = t_m \sqrt{n},(1 - t_n)$ 가 된다.

여기서 $\alpha := \sqrt{\frac{m}{n}}$라고 두면, $t_n \alpha\sqrt{n}(1 - t_m) = t_m \sqrt{n}(1 - t_n)$ 가 되고,

\[t_m = \frac{\alpha t_n}{1 - t_n + \alpha t_n} = \frac{\alpha t_n}{1 + (\alpha - 1)t_n} = \frac{\sqrt{m/n}, t_n}{1 + (\sqrt{m/n} - 1)t_n}\]

가 된다. 즉,

• $m > n$ 면 $\alpha = \sqrt{m/n} > 1$ 이므로, $t_m > t_n$가 된다.
• 즉, 픽셀 수가 더 많은 해상도 $m$에서는, 같은 “불확실성 수준”을 얻으려면 더 큰 t(=더 많은 노이즈)를 넣어야 한다는 뜻이다.

여기까지의 계산은 “상수 이미지라는 비현실적인 가정” 위에 있다.

즉, $\alpha = \sqrt{m/n}$는 이론값일 뿐이고, 실제 복잡한 이미지에서는 정확한 최적값이 아닐 수 있다.

그래서 실제로는:

• 해상도 $1024 \times 1024$에서,
• 다양한 $\alpha$ 값(예: 1.0, 1.5, 2.0, 3.0, …)을 써서 timestep을 shift해 보면서
• 생성된 이미지를 사람들에게 보여주고 어떤 $\alpha$를 더 선호하는지 human preference study를 한다.

그 결과, $\alpha$ > 1.5인 경우가 확실히 더 선호되며, 그 이후로는 별 차이가 없다.

그래서 실제로는 $\alpha = 3.0$을 채택해서, $1024×1024$ 해상도에서 학습과 샘플링 모두에 이 shift를 적용한다.

이어서, Rectified Flow / diffusion 쪽에서 log-SNR $\lambda_t$는 보통 대략 $\lambda_t = 2\log\frac{1 - t}{t}$ 같은 형태(정확한 경로에 따라 약간 변형)로 정의된다.

$\lambda_{t_n} = 2\log\frac{1 - t_n}{t_n}$, $\alpha = \sqrt{m/n}$ 이므로: $\lambda_{t_m} = \lambda_{t_n} - 2\log\alpha$

따라서 $\lambda_{t_m} = \lambda_{t_n} - \log\frac{m}{n}$ 가 된다.

즉, SNR 개념에서도 $\alpha$값 만큼 shift 하는 것

Results

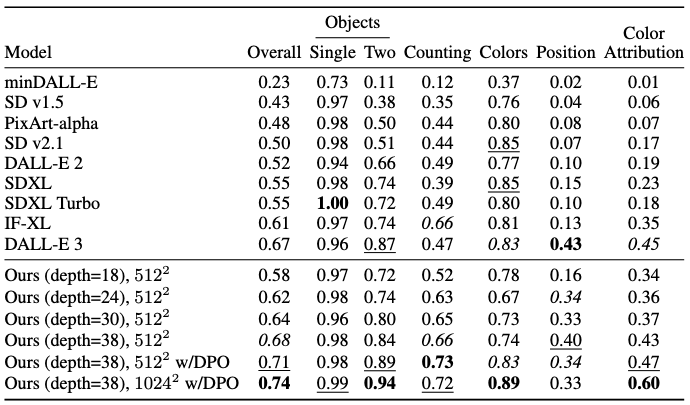
최종 8억 파라미터 SD3 모델은 다양한 benchmark에서 뛰어난 성능을 보였다.

평가로는

• T2I-CompBench (텍스트-이미지 합성 종합 benchmark)

• GenEval(프롬프트 이해 세부 평가) 점수

  

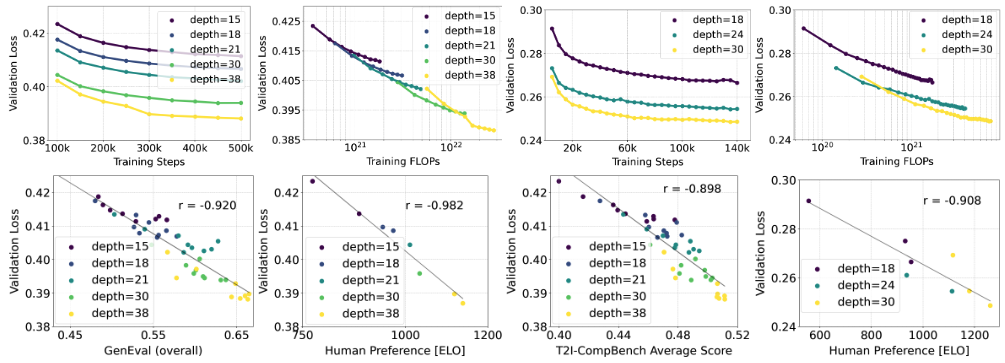
모델 크기가 커질수록 검증 loss이 감소하고 이러한 지표 점수도 향상되는 명확한 스케일링 추세가 관찰되었다.

한편 인간 평가에서도, Parti Prompts 데이터셋을 활용한 비교 실험에서 SD3 8B 모델은 시각적 품질, 프롬프트 준수, 타이포그래피 등의 항목에서 SOTA를 기록했다.

Flexible Text Enxoders

SD3에서 여러 개의 텍스트 인코더(CLIP 2개 + T5-XXL 하나)를 쓰는 기본 목적은 모델 성능을 끌어올리기 위함이다. 그런데 저자들은 이 설계가 추론 단계에서의 유연성까지 같이 준다는 점을 추가로 보여준다.

사용 텍스트 인코더:

• CLIP 기반 텍스트 인코더 2개
• T5-XXL (4.7B 파라미터짜리 초대형 모델)

학습 시, 각 텍스트 인코더에 대해 개별 드롭아웃 확률 46.3%를 둔다. 즉, 학습 중 한 스텝에서:

• 3개 모두 켜져 있을 수도 있고,
• 2개만 켜져 있을 수도 있고,
• 1개만 켜져 있을 수도 있다.

결과적으로, 모델은 “항상 3개 다 들어오는 상황”에만 의존하지 않도록 훈련된다.

학습을 이렇게 해두면, 추론 단계에서 마음대로 서브셋을 고를 수 있게 된다.

• 세 인코더를 모두 사용:
  • 메모리 많이 먹지만, 성능 최고.
• T5를 빼고 CLIP 2개만 사용:
  • VRAM 사용량 크게 절약 (T5-XXL이 4.7B라 메모리 많이 차지)
  • 대신 T5 쪽 임베딩은 0 벡터로 대체.

즉, “모델이 애초에 ‘텍스트 인코더가 부분적으로 빠진 상태’를 보고 배운 덕분에, 추론 시에도 인코더 몇 개를 꺼버려도 모델이 크게 망가지지 않는다”는 것이다.

1. T5 임베딩을 0으로 두고, CLIP 2개만 사용해도:

   • 전반적인 이미지 품질과 간단한 프롬프트 대응은 “생각보다 잘 유지”

2. 언제 T5가 정말 필요해지나?

   프롬프트가

   • 장면 설명이 매우 길고 복잡할 때, 혹은
   • 이미지 안에 텍스트(문장/단어)를 많이 포함해야 할 때

   이럴 때는 3개 인코더를 다 쓰는 편이 성능이 눈에 띄게 향상

Conclusion

이 연구를 통해 Rectified Flow라는 개념이 대규모 텍스트-투-이미지 생성 분야에서도 성공적으로 적용될 수 있음을 입증하였다.

저자들은 noise 스케줄 재가중과 듀얼 스트림 Transformer라는 두 가지 핵심 기법으로 기존 diffusion model의 한계를 뛰어넘었고, 8억 파라미터 수준 모델의 스케일링을 달성하여 개방형 모델의 새로운 지평을 열었다.

특히 적은 sampling 단계로도 높은 품질을 유지하는 효율성과 텍스트 의미 이해 및 representation력 측면에서의 강점을 모두 확보한 점이 돋보인다.

또한 검증 loss과 실제 평가 지표 간의 상관관계를 확인함으로써, 향후 더 큰 모델로의 확장이 충분히 의미 있음을 시사했다.

Limitation

1. 매우 거대한 연산 자원과 데이터가 필요

   • 8억 개의 파라미터를 훈련하고 수십만 단계 fine-tuning을 거치는 과정은 연구 기관 혹은 기업 수준의 자원을 요구하므로, 일반 연구자가 재현하기 어렵다.

2. 모델 구조의 복잡성

   • 텍스트를 위해 2~3개의 pre-training 인코더(예: 두 종류의 CLIP, T5 거대 언어모델)를 사용

   • Transformer에서도 모달별 가중치를 분리하는 등 구조가 정교

     $\rightarrow$ 메모리 요구량이 높고 구현 난이도가 상승

3. Rectified Flow의 이상적 목표인 “1-Step 생성”은 여전히 달성하지 못했다.

   • 비록 510 step의 소량 sampling으로도 기존 모델 수준의 품질을 내지만, 완전히 한 번에 이미지를 생성하는 것은 아니며, sampling 속도 향상에도 한계가 있다.

4. 개방형 평가 데이터에선 뛰어난 성능을 보였지만, 특정 영역(예: 추상 예술, 극단적으로 긴 프롬프트)에서 폐쇄형 모델을 모두 능가하는지는 추가 검증이 필요