[Paper Review] Score-based Generative model

Score-based model 논문 리뷰

arxiv : Generative Modeling by Estimating Gradients of the Data Distribution

github

데이터의 score function, 즉 데이터 분포의 기울기를 직접 모델링하는 방식을 도입한 첫번째 논문이다.

Introduction

Generative AI는 최근 두 가지 방식이 주를 이루고 있지만, 각각의 한계점이 명확하게 존재하였다.

• Likelihood-based Model
  • log-likelihood를 Object function으로 사용
  • 정규화된 확률 모델을 만들기 위해 여러 방법을 사용해야한다.
    1. 특수한 구조를 사용해 데이터의 확률 분포를 직접 modeling : Autogressive models, flow models
    2. Surrogate loss (대리 손실 함수)를 사용해 원래의 목표 함수를 대신해서 최적화 : VAE
    3. Contrastive divergence를 사용하여 모델의 에너지 함수를 학습 : Energy-based
• Generative Adversarial Networks
  • 경쟁적인 train 방식을 사용하여 모델과 데이터 간의 분포 차이를 minimize
    • 분포 차이를 $f$-divergences라 하며, 그 종류로는 KL, JS 등이 있다.
  • 위 Likelihood-based 모델의 한계를 보완하지만, Train 과정이 불안정
  • GAN의 objective는 다른 GAN 모델을 평가할 수 없다.

논문에서는 log data density인 Score(Stein)을 추정하고 sampling하는 Generative 모델의 새로운 method를 탐구한다. 데이터로부터 log density 함수의 gradient를 학습하기 위해 score mathing 모델을 사용한다. 그런 다음, Langevin dynamics(랑주뱅 역학)을 사용하여 sample을 생성하며, 이는 초기 sample을 Score에 따라 점차 density가 높은 역영역으로 Transition하는 방식으로 작동한다.

Score(Stein)

이전 생성모델들은 log likelihood의 gradient인 $\nabla_\theta \log p_\theta(x)$을 통해 $\theta$를 업데이트하는 방식이었다.

하지만, Score-Based 모델은 학습 데이터 $x$ 자체의 gradient을 구하는 Stein Score Function을 바탕으로 학습을 진행한다.

\[s_\theta(x) = \nabla_x \log p_\theta(x)\]

즉, Score function이란 데이터 $x$의 분포를 기준으로 likelihood가 높은 방향으로 gradient를 유도하는 알고리즘이다.

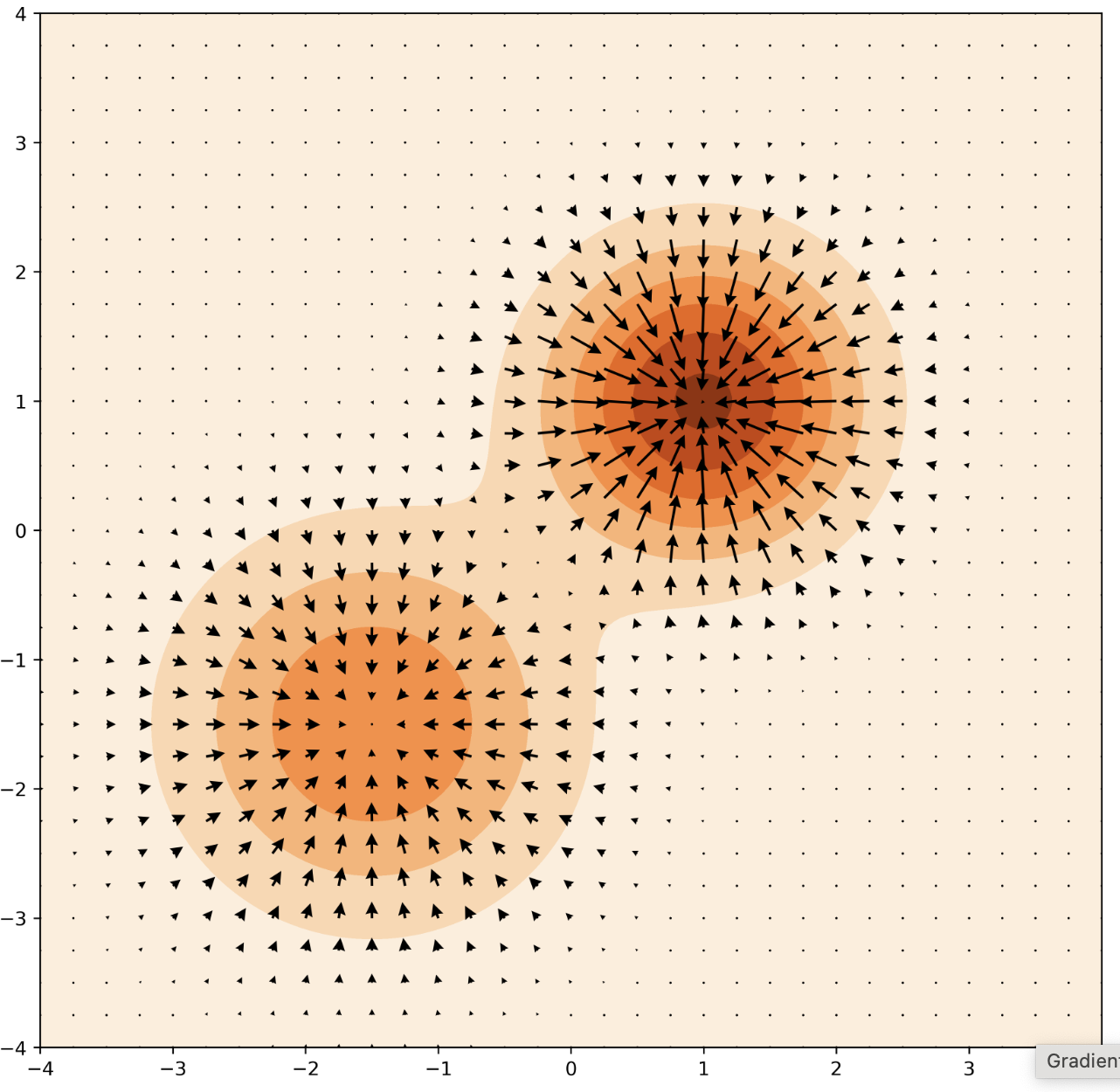
여기서 score는 각 지점에서 어떻게 움직여야 likelihood가 높은 지점으로 갈 수 있는지를 알려주는 역할을 한다. 따라서 위 분포에서는 화살표(score)를 따라가면 각각의 Gaussian의 mean vector에 도착하게 된다.

Score-based model의 핵심아이디어는 확률분포함수를 사용하는 대신 이 score를 활용하는 것이다.

Langevin dynamics

랑주뱅 동역학은 분자 시스템의 움직임의 수학적 모델링이다. 확률적 미분 방정식을 사용해 자유도를 생략하면서 단순화된 모델을 사용한다.

Problem

하지만, 이러한 접근 방식에는 다음과 같이 해결해야하는 과제 2가지가 있다.

1. 저차원 maniford에서의 데이터셋 분포는 score가 주변 space에서 정의되지 않으며 score matching이 일관된 추정치를 제공하지 않는다.
2. low-density 영역의 데이터가 부족할 경우, score matching 정확도가 떨어지고 Langevin dynamics sampling의 mixing 속도가 감소한다.

Langevin dynamics는 밀도가 낮은 영역에서 자주 초기화됨

이 2가지 문제는 초기 sample을 high-density 영역으로 transition할 때 발생한다.

위 사진처럼 좌측 하단 distribution에서 우측 상단 distribution으로 transition하며 추가적인 특징을 가진 이미지를 생성하려고 한다. 중간 대각선 영역은 low density 영역이며 score가 존재하지 않는다. 때문에 이 영역을 지나야 하지만, score가 존재하지 않기 때문에 어느 방향으로 가야할 지를 모르는 문제가 생긴다. 이를 모델이 저차원 manifold에서 “collapse”된다고 표현한다.

Solution

위 문제를 해결하기 위해 데이터에 random Gaussian noise를 추가하여 collapse를 방지한다. Noise level이 클수록 데이터 분포의 low density 영역에서 sample을 생성하여 score matching을 개선한다.

논문에서는 Annealed version of Langevin dynamics을 제안하는데, 이는 처음에는 높은 level의 nosie를 추가하고, Noise level을 점차 낮추며 추가하는 방법이다.

Score-based Generative modeling

데이터셋을 $p_{data}(x)$에서 sampling된 i.i.d.한 $\lbrace x \in \mathbb{R}^D \rbrace^{N}_{i=1}$으로 가정하자.

i.i.d.란 independent and identically distribution의 약어로 독립 항등분포, 즉 독립적이고 같은 확률 분포를 가지는 것을 말한다.

PDF인 $p(x)$의 score를 $\nabla_x \log p(x)$로 정의되며 score network $s_\theta : \mathbb{R}^D \rightarrow \mathbb{R}^D$는 $\theta$로 parameterize된 Neural network이다. 이 신경망은 $p_{data}(x)$의 score를 근사화하도록 훈련된다.

이 Score-based generative modeling framwork에는 score matching과 Langevin dynamics라는 두가지 요소가 있다.

Score matching for score estimation

score matching을 사용하면, $p_{data}(x)$를 추정하는 모델 없이 score network $s_\theta$를 train하여 $\nabla_x \log p_{data}(x)$를 추정할 수 있다.

즉, $\theta$라는 파라미터를 지닌 모델을 활용하여 $\nabla_x \log p_{\theta}(x)$를 $\nabla_x \log p_{data}(x)$가 되도록 train하는 것이 Score-based의 아이디어이다.

즉 $s_\theta (x) = \nabla_x \log p_{\theta}(x)$가 $\nabla_x \log p_{data}(x)$와 같아지도록 하기 위해 Euclidean distance로 정의한 Objective은 다음을 minimize한다.

\[\frac{1}{2}\mathbb{E}_{p_{data}} \left [\left|\left| s_\theta(x) - \nabla \log p_{\text{data}}(x) \right|\right|^2_2 \right]\]

위 식을 Fisher Divergence라고 한다.

위 식은 부분적분을 통해 다음과 같이 유도할 수 있다. (우리가 모르는 $p_{\text{data}}(x)를 없애기 위해) (이과정이 score matching이다.)

\[\mathbb{E}_{p_{data}} \left [\text{tr}(\nabla_xs_\theta(x)) + \frac{1}{2}\left|\left| s_\theta(x) \right|\right|^2_2 \right] \tag{1}\]

Eq. 1유도 과정

$$ \begin{align} \frac{1}{2}\mathbb{E}_{p_{data}} \left [\left|\left| s_\theta(x) - \nabla \log p_{\text{data}}(x) \right|\right|^2_2 \right] &= \frac{1}{2} \int p(x)(\nabla_x \log p(x) - s_\theta(x))^2 \text{d}x \nonumber\\ &= \frac{1}{2} \int p(x)(\nabla_x \log p(x))^2\text{d}x + \frac{1}{2} \int p(x)s_\theta(x)^2 \text{d}x - \int p(x) \nabla_x \log p(x)s_\theta(x) \text{d}x \nonumber \end{align} $$ 여기서 마지막 항 $- \int p(x) \nabla_x \log p(x)s_\theta(x) \text{d}x$는 다음과 같이 유도할 수 있다. $$ \begin{align} - \int p(x) \nabla_x \log p(x)s_\theta(x) \text{d}x &= - \int p(x) \frac{\nabla_xp(x)}{p(x)}s_\theta(x)\text{d}x \nonumber\\ &= -\int \nabla_x p(x)s_\theta(x) \text{d}x \nonumber\\ &= -p(x)s_\theta(x) |^\infty_{x=-\infty} + \int p(x)\nabla_xs_\theta(x)\text{d}x \nonumber\\ &= \int p(x)\nabla_x s_\theta(x)\text{d}x \nonumber \end{align} $$ 3번째 줄에서 boundary term은 $\pm\infty$에 의해 0이 된다. 즉 마지막 항을 $\int p(x)\nabla_x s_\theta(x)\text{d}x$으로 유도함으로써 $\frac{1}{2}\mathbb{E}_{p_{data}} \left [\left|\left| s_\theta(x) - \nabla \log p_{\text{data}}(x) \right|\right|^2_2 \right]$는 다음과 같이 유도할 수 있다. $$ = \underbrace{\frac{1}{2} \int p(x)(\nabla_x \log p(x))^2\text{d}x }_{1}+ \underbrace{\frac{1}{2} \int p(x)s_\theta(x)^2 \text{d}x}_2 + \underbrace{\int p(x)\nabla_x s\_\theta(x)\text{d}x}_3 $$ 여기서 1번 항을 $\theta$에 대해 independent하기 때문에 상수로 바꾸고 2, 3번 항을 각각 $\mathbb{E}$로 묶으면 다음과 같은 식이 된다. $$ C + \frac{1}{2}\mathbb{E}_{p(x)} [s_\theta(x)^2] + \mathbb{E}_{p(x)}[\nabla_xs_\theta(x)] $$

$\nabla_x s_\theta(x)$는 $s_\theta(x)$의 Jacobian matrix를 나타낸다.

Jacobian matrix란, 다변수 함수의 도함수를 나타내는 행렬이다. 다변수 함수의 입력 변수가 여러 개일 때, 각 입력 변수에 대한 편미분 값을 행렬로 정리한 것을 말한다.

이 Jacobian matrix는 Deep network와 고차원 데이터에서 계산이 어렵기 때문에 다음과 같은 Score matching method 2가지를 설명한다.

Denoising score matching

Denoising score matching은 $\text{tr}(\nabla_x s_\theta(x))$의 계산을 우회하는 변형된 score matching이다. 데이터 $x$에 nosie distribution $q_\sigma (\widetilde{x} | x)$를 추가하고, 이를 제거하는 방식으로 진행한다.

noise가 추가된 데이터 distribution $q_\sigma (\widetilde{x}) \triangleq \int q_\sigma (\widetilde{x} | x)p_{data}dx$의 score를 추정하며, Objective는 다음과 같다.

\[\frac{1}{2} \mathbb{E}_{q_\sigma(\widetilde{x}|x)p_{data}(x)}\left [\left|\left| s_\theta(\widetilde{x}) - \nabla_{\widetilde{x}}\log q_\sigma(\widetilde{x}|x) \right|\right|^2_2 \right] \tag{2}\]

최적의 score 모델은 위 식 Eq. (2)를 minimize하여 $s_{\theta^*}(x) = \nabla_x \log q_\sigma (x)$를 만족하는 $s_{\theta^*}(x)$이다.

Sliced score matching

Sliced score matching은 random projection을 사용하여 $\text{tr}(\nabla_xs_\theta(x))$의 근사치를 구한다.

Data score와 모델 분포의 vector field가 scalar 필드가 되도록 score를 random한 방향으로 projection한 다음 scalar 필드를 비교하여 모델 분포가 데이터 분포에서 얼마나 떨어져 있는지 확인한다.

radom projection 방향을 $\textbf{v}$로, $\textbf{v}$의 분포를 $p_{\textbf{v}}$로 할때, random projection에 대한 Fisher Divergence는 다음과 같다.

\[\frac{1}{2} \mathbb{E}_{p_{\text{data}}}[(\textbf{v}^\top\nabla_x \log p_{\text{data}}(x) - \textbf{v}_\top \nabla_x \log p_\theta(x))^2]\]

$s_\theta(x) = \nabla_x \log p_\theta(x)$이므로 아래 식과 동일

\[\frac{1}{2} \mathbb{E}_{p_{\text{data}}}[(\textbf{v}^\top\nabla_x \log p_{\text{data}}(x) - \textbf{v}_\top s_\theta(x))^2]\]

위 식 역시 Eq. 1을 유도한 trick을 사용하여 다음과 같이 나타낼 수 있다.

\[\mathbb{E}_{p_\textbf{v}}\mathbb{E}_{p_\text{data}} \left[\textbf{v}^\top \nabla_xs_\theta(x)\textbf{v} + \frac{1}{2}\left|\left| s_\theta(x) \right| \right| ^2_2 \right] \tag{3}\]

Sampling with Langevin dynamics

Langevin dynamics는 score function $\nabla_x \log p(x)$를 사용하여 sampling한다.

$\textbf{z}_t \sim \mathcal{N}(0, \mathit{I})$일때 다음과 같다.

\[\widetilde{x}_t = \widetilde{x}_{t-1} + \frac{\epsilon}{2} \nabla_x \log p(\widetilde{x}_{t-1}) + \sqrt{\epsilon}\;\textbf{z}_t \tag{4}\]

이 sampling 과정에서 $\nabla_x \log p(x)$가 필요하기 때문에, $s_\theta(x) \approx \nabla_x \log p(x)$가 되도록 train 한 다음, 이 $s_\theta$를 사용하여 sampling을 진행한다.

Challenges of score-based generative modeling

이 section에서는 Score-based 방식의 2가지 장애물을 다룬다.

1. The manifold hypothesis

위에서 언급했듯이, 데이터가 저차원 manifold에 있는 경우, score가 well-define되지 않고, model이 collapse될 수 있다.

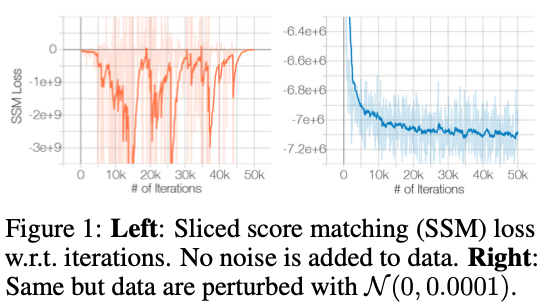
Figure 1을 보자.

왼쪽 그래프는 원본 CIFAR-10로 train한 Sliced score matching의 loss로 불규칙적인 변화를 보인다.

이를 방지하기 위해 Gaussian noise를 추가하는데, 오른쪽 그래프를 보면 loss값들이 수렴하는 것을 볼 수 있다.

2. Low data density regions

low density 영역의 데이터 부족은 score matching을 통한 score estimate와 Langevin dynamics을 이용한 MCMC samping에 어려움을 야기한다.

1. Inaccurate score estimation with score matching

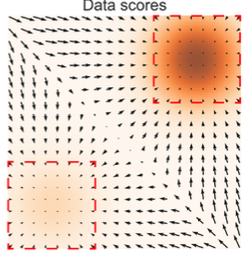
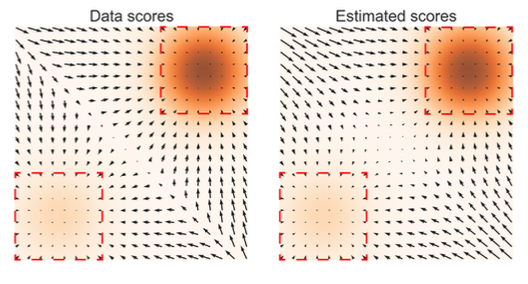
low density 영역에서는 Eq. 2를 minimize하는 score matching을 통해 score function이 잘 추정되지 않는다.

위 사진에서 실제 데이터 score (왼쪽)와 추정된 score (오른쪽)의 중앙을 보면 score가 제대로 구해지지 않았다는 것을 볼 수 있다. 해당 영역에서의 score estimation은 매우 부정확해지며, Score estimation이 부정확하면 결국 Langevin dynamics을 통한 sampling 과정도 부정확해지게 될 것이다.

2. Slow mixing of Langevin dynamics

다른 두 데이터 분포를 mix할 때 그 비율을 알 수 없다는 문제도 발생한다.

$p_{\text{data}}$가 다음과 같이 $p_1$과 $p_2$ 분포의 mixture로 구성된 데이터 분포라고 가정하자.

\[p_{\text{data}}(x) = \pi p_1(x) + (1-\pi)p_2(x)\]

$\nabla_x \log p_{\text{data}}(x)$를 구하기 위해서 각 항에 $\log$를 씌우면, 각각 $\log \pi$와 $\log (1-\pi)$는 상수가 되어버리므로, 결국 다음과 같이 된다.

\[\nabla_x \log p_{\text{data}}(x) = \nabla_x \log p_1(x) + \nabla_x \log p_2(x)\]

즉, mixture 비율(즉 가중치)인 $\pi$에 상관없이 score가 추정된다.

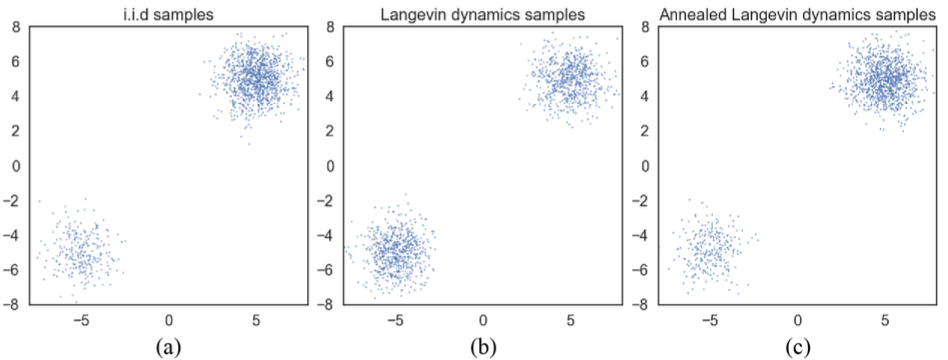
위 그림에서 (a)는 원래 데이터 분포이며, 두 분포가 다른 비율로 mixture된 것을 알 수 있다.

(b)는 Langevin dynamics으로 sampling된 결과이며, 두 분포가 균일하게 samping된 것을 볼 수 있다.

(c)는 annealed된 Langevin dynamics으로 sampling된 결과이며, mixture 비율을 반영한 것이다.

Noise Conditional Score Networks : learning and inference

논문에서는 Gaussian Noise를 추가한 경우, Score-based 모델링의 성능이 높아진다는 것을 발견하였다. 그 이유는 크게 다음과 같은 2가지가 있다.

1. Gaussian noise의 support가 하나의 whole space이기 때문에 저차원 maniford에 제한받지 않게 되어 score matching이 수월하게 define된다.
2. Gaussian nosie를 추가함으로써 low density 영역을 채워주기 때문에 score estimation을 개선할 수 있다.

1. Noise Conditional Score Networks

$\lbrace\sigma_i\rbrace^L_{i=1}$를 $\frac{\sigma_1}{\sigma_2} = \cdots = \frac{\sigma_{L-1}}{\sigma_L} > 1$를 만족하는 수열이라고 하자. 이 각각의 $\sigma$가 바로 level에 따른 nosie가 된다.

$\sigma_1$의 경우 매우 큰 nosie이며 $\sigma_L$에 가까워질 수록 데이터에 영향을 거의 미치지 않는 작은 수준의 nosie이다.

\[q_\sigma(x) \triangleq \int p_{data}(\textbf{t})\mathcal{N}(x | t, \sigma^2\textit{I})d\textbf{t}\]

$q_\sigma(x)$를 위와 같이 timestep $\textbf{t}$에 따라 nosie가 부여된 데이터의 분포라고 정의하면, 이 데이터 분포를 이용하여 score를 추정하는 network는 다음과 같다.

\[\forall \sigma \in \lbrace\sigma_i\rbrace^L_{i=1} : s_\theta (x, \sigma) \approx \nabla_x \log q_\sigma(x)\]

이때 $x \in \mathbb{R}^D$, $s_\theta (x, \sigma) \in \mathbb{R}^D$이다.

위와 같은 $s_\theta (x, \sigma)$를 Noise Conditional Score Network(NCSN)이라 부른다.

NCSN에서 사용한 아키텍쳐의 특징으로는 U-Net과 Instance Normalization이 있다.

2. Learning NCSNs via score matching

위 언급한 두 score matching 기법 모드 NCSN를 train할 수 있지만, noise있는 데이터를 다루고 속도가 약간 더 빠른 Denoising score matching을 사용하였다고 한다.

Noise 분포 $q_\sigma(\widetilde{x} \;| \;x) = \mathcal{N}(\widetilde{x}\; | x, \sigma^2 \textit{I})$ 를 사용하면 score function은 다음과 같다.

\[\nabla_{\widetilde{x}} \log q_\sigma(\widetilde{x} \;| \;x) = -\frac{\widetilde{x}-x}{\sigma^2}\]

Why??

Gaussian 분포 $p(x)$는 $p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$로 정의되며, 이에 대한 score function은 위 $p(x)$에 $\log$를 씌우고 $x$에 대해 편미분을 진행한 $\nabla_x \log p(x)$이며 다음과 같다. $$ \begin{align} \nabla_x \log p(x) &= \nabla_x \left (\log\frac{1}{\sqrt{2\pi\sigma^2}} + -\frac{(x-\mu)^2}{2\sigma^2} \log e \right) \nonumber \\ &= -\frac{x-\mu}{\sigma^2} \nonumber \end{align} $$ 여기에 우리는 Noise가 추가된 조건부 Gaussian 분포 $p(\widetilde{x} | x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(\widetilde{x}-x)^2}{2\sigma^2}}$를 정의한다. 이렇게 정의된 조건부 Gaussian 분포의 평균은 $x$가 되는데, 그 이유는 분포가 주어진 조건부 $x$를 중심으로 sampling이 이루어지기 때문이다. 즉 $p(\widetilde{x} | x) = \mathcal{N}(\widetilde{x} | x, \sigma^2 \textit{I})$로 정의할 수 있으며, 위와 같이 처리하면 $ -\frac{\widetilde{x}-x}{\sigma^2}$를 얻을 수 있다.

noise인 $\sigma$가 주어졌을 때, denoising score matching의 Objective(Eq. 2)는 다음과 같다.

\[\mathscr{l}(\theta; \sigma) \triangleq \frac{1}{2} \mathbb{E}_{p_{\text{data}}(x)} \mathbb{E}_{\widetilde{x} \sim \mathcal{N}(x, \sigma^2, \textit{I})} \left[\left|\left|s_\theta(\widetilde{x}, \sigma) + \frac{\widetilde{x} - x}{\sigma^2} \right|\right|^2_2 \right] \tag{5}\]

여기에 $\sigma \in \lbrace\sigma_i\rbrace^L_{i=1}$을 결합하여 timestep에 대해 정의하면 Unified objective를 얻을 수 있다.

\[\mathcal{L}(\theta ; \lbrace\sigma_i\rbrace^L_{i=1}) \triangleq \frac{1}{L} \sum_{i=1}^L \lambda(\sigma_i) \mathscr{l}(\theta, \sigma_i) \tag{6}\]

여기서 $\lambda(\sigma)$는 $\sigma$에 의한 계수 함수(coefficient function)이다.

이상적으로 모든 $i$에 대해 $\lambda(\sigma_i) \mathscr{l}(\theta, \sigma_i)$가 동일하기 위해 경험적으로 $\lambda(\sigma) = \sigma^2$을 얻어낼 수 있었다고 한다.

3. NCSN inference via annealed Langevin dynamics

NCSN $s_\theta(x, \sigma)$를 train 한 후, 이번 section에서는 sampling 과정인 Annealed Langevin dynamics인 Algorithm 1을 제안한다.

고정된 분포 $x_0$에서 시작하여 $q_{\sigma_{i}}(x)$와 step size $\alpha_i$를 통해 $q_{\sigma_{i+1}}(x)$를 만든다. step size $a_i$는 위 3번째 줄 식을 통해 점차 감소시키며, 마지막에 $q_{\sigma_{L}}(x)$로부터 만들어진 sample은 $p_{\text{data}}(x)$와 비슷해진다.

이때 noise level은 거의 없는 수준이다. $\rightarrow \sigma_L \approx 0$

Gaussian Noise가 첨가된 분포인 $\lbrace q_{\sigma_i} \rbrace ^L_{i=1}$은 whole space에 걸쳐 있기 때문에 density가 높다고 할 수 있다. score estimation과 Langevin dynamics는 high-density 영역에서 매우 잘 수행되므로 처음에 언급한 문제 2가지를 해결할 수 있다고 논문에서 말한다.

$a_i$를 조정하는 다양한 방법이 있지만, 논문에서는 $\alpha_i \propto \sigma_i^2$를 채택하였다고 한다. 그 이유는 Langevin dynamics에서 signal-to-noise 비율을 고정하는 것에서 비롯되었다. ($\frac{\alpha_i s_\theta(x, \sigma_i)}{2\sqrt{\alpha_i}\;z}$)

\[\mathbb{E} \left[ \left|\left| \frac{\alpha_i s_\theta(x, \sigma_i)}{2\sqrt{\alpha_i}\;z} \right|\right|^2_2 \right] \approx \mathbb{E} \left[ \frac{\alpha_i \left|\left|s_\theta(x, \sigma_i) \right|\right|^2_2}{4} \right] \propto \frac{1}{4} \mathbb{E} \left[\left|\left| \sigma_i s_\theta(x, \sigma_i) \right|\right|^2_2 \right]\]

위 관계를 기억하자. 앞에서 우리는 $\left|\left| s_\theta(x, \sigma) \right|\right|_2 \propto \frac{1}{\sigma}$일때 Score network 학습이 optimal 해진다는 것을 찾았다.

(그렇지 않은 경우에는 $\mathbb{E} \left[\left|\left| \sigma_i s_\theta(x, \sigma_i) \right|\right|^2_2 \right] \propto 1$)

그러므로 위 관계는 다음과 같이 되어 $\sigma_i$와 무관해진다.

\[\left|\left| \frac{\alpha_i s_\theta(x, \sigma_i)}{2\sqrt{\alpha_i}\;z} \right|\right|^2_2 \propto \frac{1}{4} \mathbb{E} \left[\left|\left| \sigma_i s_\theta(x, \sigma_i) \right|\right|^2_2 \right] \propto \frac{1}{4}\]

위 Algorithm 1의 효율성을 입증하기 위해 실험을 진행하였으며, 그 결과를 section 3.2에서 설명하였듯이 Annealed Langevin dynamics는 두 mode간의 가중치를 반영하여 복구한 것을 볼 수 있다.

Sampling은 Annealed Langevin dynamics로 진행한다면, score estimator 역시 noise가 추가된 sample로 학습을 해야 정확한 score가 추정된다.

때문에, sample에 다양한 크기의 nosie($\mathcal{N}(0, \sigma_i^2\textit{I})$)를 추가하여 학습시키는데, 이때 추가하는 noise의 크기는 갈수록 증가한다. ($\sigma_1 < \sigma_2 < \cdots < \sigma_L$, sampling의 정반대)

sample은 데이터 $x \sim p(x)$에 noise $z \sim \mathcal{N}(0, \textit{I})$를 더한 $x + \sigma_i z$로 만들며 NCSN 모델 $s_\theta (x, i)$를 학습시킨다.

\[p_{\sigma_i}(x) = \int p(y)\mathcal{N}(x;y, \sigma_i^2,\textit{I})\text{d}y\]

여느 Conditional 모델처럼 $\sigma$(더해지는 nosie level)가 입력으로 들어가기 때문에 $s_\theta(x, i) : \mathbb{R}^{D+1} \rightarrow \mathbb{R}^D$가 된다.

$s_\theta(x, i)$의 Objective는 다음과 같다. (Denoising score matching 기반이며 noise인 $\sigma$가 추가됨)

\[\sum_{i=1}^L \lambda(i) \mathbb{E}_{p_{\sigma_i}(x)}\left[|| \nabla_x \log p_{\sigma_i}(x) - s_\theta(x, i)||^2_2\right]\]

이러한 train과정을 거치면 Annealed Langevin dynamics를 통해 sampling을 진행하면 된다.

Experiments

Set up

• 사용 데이터셋 : MNIST, CelebA, CIFAR-10
• [0, 1] 범위로 scaling
• Noise $\sigma \in \lbrace\sigma_i\rbrace^L_{i=1}$가 $1 \sim 0.01$이 되도록 $L = 10$으로 설정 ($\sigma_L = 0.01$은 육안으로 거의 구분 불가)
• $T = 100$, $\epsilon = 2 \times 10^{-5}$
• Architecture 특징 : U-net, Conditional Instance normalization, Dilated convolutions

Yang song은 Score-based model을 학습할 때 다음과 같은 사항을 추천했다.

• $\sigma_1 < \cdots < \sigma_L$은 기하수열로 구성
• $\sigma_1$은 충분히 작은 값에서 시작하여야 하며 $\sigma_L$은 데이터의 maximum pairwise distance 수준으로 결정
• $L$은 주로 수백 ~ 수천의 크기로 설정

NCSN 모델이 CelebA와 CIFAR-10 데이터셋으로 학습시켜 sampling하는 결과를 보여준다.

Conclusion

이번 논문에서는 Score-based Generative model의 기본 원리에 대해 탐구해보다. 이 모델은 기존의 GAN, VAE와 같은 방식이 아닌 새로운 생성 모델 프레임워크로서, score라는 개념을 중심으로 새로운 패러다임을 제시한다. CIFAR-10에서 inception score SOTA를 달성하였으며, SNGAN에 필적하는 FID score를 얻었다고 한다.

Code