Post

[Paper Review] SigLIP

Posted Updated
By HahnGyuTak 35 min read

[논문 리뷰] Sigmoid Loss for Language Image Pre-Training

Sigmoid Loss for Language Image Pre-Training

Xiaohua Zhai et al

ICCV 2023

[arXiv] [Github]

Background

Contrastive Learning

은 pair으로 주어진 데이터에서 일치하는 pair은 임베딩 공간에서 가깝게 끌어당기고, 일치하지 않는 pair은 멀어지도록 학습하는 방법이다.

예를 들어, 이미지와 텍스트 캡션의 pair으로 학습할 경우, 모델은 이미지-텍스트 임베딩을 서로 정렬하여 맞는 이미지는 맞는 캡션과 가깝게, 무관한 캡션과는 멀어지도록 표현을 학습한다 .

OpenAI의 CLIP 등 선도적인 연구들은 이러한 이미지-텍스트 contrastive learning을 대규모로 적용하여 강력한 zero-shot 모델을 구현했고, 인터넷에서 수집한 거대한 이미지-텍스트 페어 데이터셋을 활용하면 모델과 데이터 규모에 비례해 성능이 향상됨을 보여주었다.

그러나 CLIP 방식에는 두 가지 기술적 과제가 있다.

  1. 높은 성능을 위해 매우 큰 batch size가 필요

    • CLIP 논문에서는 한 번의 학습 스텝에 32k 개의 이미지-텍스트 pair을 사용
    • 많은 negative 사례와 비교하여 학습해야 하므로 배치가 커질수록 유리
      • 메모리 한계와 연산 비용의 문제로 이어진다.

  2. 다수의 GPU에 배치를 나누어 처리할 때 각 임베딩을 교환해야 하는 통신 비용(communication)이 매우 큼

    • 구체적으로, CLIP에서는 모든 GPU가 서로의 이미지와 텍스트 임베딩을 실시간으로 all-gather하여 전체 배치의 유사도 행렬($N×N$)을 계산

    • GPU 256개로 5~10일간 학습해야 하는 등 학습 비용이 매우 높다.

      이러한 문제를 완화하기 위해

      • MoCo는 메모리 큐로 과거 배치의 임베딩을 활용
      • SimSiam은 stop-gradient 기법으로 contrastive learning 단계에서 negative 샘플을 아예 사용하지 않음

      등 여러 시도가 있었다 .

Introduction

SigLIP은 CLIP에서 쓰이던 softmax 기반 contrastive loss를 sigmoid 기반 pair별 binary classification loss로 대체하여, 배치 전역 정규화와 전원 경쟁 없이 각 이미지–텍스트 pair 단위로 loss를 계산하도록 한다.

이로써 $N\times N$ 유사도 행렬을 항시 유지할 필요가 줄어 메모리 사용과 통신 부하가 감소되고, 작은 배치에서도 안정적으로 학습되며 필요하면 큰 배치로도 유연하게 확장된다.

스크린샷 2025-09-02 오후 4.37.33

실제로 저자들은 LiT와 결합한 SigLiT 설정에서 4개의 TPUv4로 2일 만에 ImageNet zero-shot 84.5%를 달성하여 학습 효율을 입증했다.

또한 배치 크기를 최대 100만까지 확장해 분석한 결과, 약 32k 수준에서 성능이 포화되는 경향을 확인하여 “초대형 배치 의존”을 완화할 수 있음을 보였다.

요컨대 SigLIP은 loss 설계만으로 배치·통신 병목을 완화하고 안정성·효율·성능을 함께 끌어올리는 접근이라 할 수 있다.

Goal

  • 언어–이미지 사전학습에서 Global normalization 없이 pair 별 판별로 효율적·안정적 정렬 임베딩을 학습하도록 한다.
  • 자원 제약 환경에서도 높은 zero-shot 성능을 달성 가능한 실용적 레시피를 제시한다.

Motivation

  • softmax contrastive loss의 큰 배치·큰 통신·큰 메모리 의존성을 줄일 필요가 있다.
  • 웹 스케일 데이터의 노이즈·불균형 하에서도 안정적 학습을 가능하게 하는 loss이 요구된다.
  • 동일 자원 대비 더 나은 효율/성능을 내는 대안적 contrastive loss이 필요하다.

Contribution

  • Sigmoid 기반 pair별 loss을 제안하여 전역 정규화 제거 및 메모리·통신 비용 절감
  • LiT 결합(SigLiT) 및 from-scratch 설정에서 작은 칩 수·짧은 시간으로 경쟁적 zero-shot 성능을 달성
    • 예: 4×TPUv4, 2일, 84.5%
  • 초대형 배치 실험(최대 1e6)으로 약 32k에서 성능 포화를 관찰, 과도한 배치 확장을 재고할 근거를 제시
  • 멀티설정(싱글/멀티링구얼)에서 작은 배치 우위 및 대규모 스케일링의 한계를 체계적으로 분석

Method

Softmax Contrastive Learning

contrastive learning 목표는 주어진 미니배치 $B={(I_1, T_1), (I_2, T_2), … (I_{B}, T_{B})}$에서 positive pair 이미지 $I_i$와 텍스트 $T_i$는 가깝게, negative pair $I_i$–$T_j$ (단 $j \neq i$)는 멀어지도록 임베딩을 조정하는 것이다.

기존 CLIP 등의 softmax 기반 contrastive loss은 이를 다음과 같이 구현한다.

  1. 우선 이미지 인코더 $f(\cdot)$와 텍스트 인코더 $g(\cdot)$를 통해 각각 이미지 $I_i$와 텍스트 $T_j$의 임베딩을 얻어 내적 유사도 $\langle x_i, y_j\rangle$를 계산
  2. softmax 정규화를 통해 이미지→텍스트 방향과 텍스트→이미지 방향 각각에 대한 교차 엔트로피 loss을 구한다.

식으로 나타내면 아래와 같다.

\[L_{\text{image→text}} = -\frac{1}{|B|}\sum_{i=1}^{|B|}\log \frac{\exp!\big(t \cdot \langle x_i,;y_i\rangle\big)}{\sum_{j=1}^{|B|}\exp!\big(t \cdot \langle x_i,;y_j\rangle\big)},\] \[L_{\text{text→image}} = -\frac{1}{|B|}\sum_{i=1}^{|B|}\log \frac{\exp!\big(t \cdot \langle x_i,;y_i\rangle\big)}{\sum_{j=1}^{|B|}\exp!\big(t \cdot \langle x_j,;y_i\rangle\big)},\]

여기서 $t$는 온도 파라미터(temperature)로, 출력 분포의 날카로움을 조절하는 값이다 . 최종 loss $L_{\text{softmax}}$는 위 두 항의 평균으로 정의된다 ($L_{\text{softmax}} = \frac{1}{2}(L_{\text{image→text}} + L_{\text{text→image}})$).

이 softmax contrastive loss에서 각 이미지는 배치 내 모든 텍스트들 중 정답 텍스트만 높은 점수를 갖도록 학습되며, 반대로 각 텍스트도 모든 이미지 중 정답 이미지와 가장 가깝도록 학습된다.

  • 위 식의 분모를 보면 배치의 전원합(sum over batch)으로 확률을 정규화
    • 이 때문에 각 step마다 배치 전체의 유사도 행렬을 필요로 하여 메모리와 연산 비용이 이차적으로 증가
  • 이미지→텍스트, 텍스트→이미지 두 방향의 loss를 별도로 계산
    • 수식이 비대칭(asymmetric)
    • 실제 구현 시에는 이를 위해 임베딩 행렬을 복제해 두 번 계산

Sigmoid loss for language image pre-training

이에 반해 sigmoid 기반 loss(SigLIP)은 배치 내 모든 이미지-텍스트 pair을 이진 분류하는 것으로 문제를 재구성한다.

각 pair $(I_i, T_j)$에 대해 정답 여부를 나타내는 레이블 $z_{ij}$를 정의하며, $z_{ij}=1$이면 짝이 맞는 pair (즉 $j=i$인 경우), $z_{ij}=0$이면 짝이 틀린 pair이다.

이제 모델이 산출한 유사도(score) $s_{ij} = t \cdot \langle x_i,;y_j\rangle + b$에 대해 sigmoid 함수 $\sigma(s) = 1/(1+e^{-s})$를 적용하여 해당 pair이 정답일 확률로 해석한다.

$t$는 학습되는 온도 파라미터이고, $b$는 SigLIP에서 새로 도입된 바이어스 항이다.

그런 다음 각 pair마다 이진 교차 엔트로피 loss을 계산한다.

예를 들어

  • 정답인 pair $(i=i)$에 대해서는 예측 확률 $\sigma(s_{ii})$가 1에 가까울수록 좋음

    → loss $-\log(\sigma(s_{ii}))$을 부여

  • 오답인 pair $(i \neq j)$에 대해서는 예측 확률 $\sigma(s_{ij})$가 0에 가까울수록 (즉 $1-\sigma(s_{ij})$가 클수록) 좋음

    → loss $-\log(1-\sigma(s_{ij}))$를 부여

\[-\frac{1}{|B|}\sum_{i=1}^{|B|}\sum_{j=1}^{|B|}\underbrace{\log \frac{1}{1+e^{-z_{ij}(-t,x_i\cdot y_j+b)}}}_{\mathcal{L}_{ij}}\]

  • $|B|$: 배치 크기(샘플 쌍 개수), 종종 $n$으로 둔다

  • $x_i=\frac{f(I_i)}{|f(I_i)|_2},\;y_j=\frac{g(T_j)}{|g(T_j)|_2}\in\mathbb{R}^d$: L2 정규화된 이미지/텍스트 임베딩

  • $t$: learnable temperature 스칼라(보통 $t=\exp(t’)$로 파라미터화)

  • $b$: learnable bias 스칼라(초기 불균형 완화를 위해 도입)

  • $z_{ij}\in{+1,-1}$: 레이블

  • $\mathcal{L}_{ij}=\dfrac{1}{1+e^{-z_{ij}(-t,x_i\cdot y_j+b)}}$: 쌍 $(i,j)$에 대한 sigmoid 항

    $\log \mathcal{L}_{ij}=\log\sigma\big(z_{ij}(t,x_i\cdot y_j+b)\big)$, $\ \sigma(u)=\dfrac{1}{1+e^{-u}}$

이렇게 모든 pair에 대한 loss를 합산 후 평균 내면 최종 sigmoid contrastive loss $L_{\text{sigmoid}}$가 얻어진다.

직관적으로, 이 loss은 “각 이미지-텍스트 pair가 정답인지 여부를 맞히는 N²개의 이진 분류 문제”로 볼 수 있다.

softmax 방식과 달리 한 pair의 예측 결과가 다른 pair의 loss에 영향을 주지 않으므로, 배치 내 pair들이 독립적인 형태로 학습된다.

이는 계산상 큰 이점으로, 배치 크기에 따른 전역 정규화 항을 없앴기 때문에 큰 배치에 대한 메모리 병목을 제거하고 작은 배치에서도 안정적 학습이 가능하게 해준다 .

다만 이렇게 하면 학습 초기에 positive/negative pair 비율의 불균형 때문에 loss 값이 지나치게 커질 우려가 있다 .

배치 크기가 $N$일 때 단 $N$개의 positive pair과 $N(N-1)$개의 negative pair이 존재하므로, 초기에는 모델이 모든 pair을 negative으로 예측하는 쪽으로 크게 치우칠 수 있다.

이를 막기 위해 SigLIP에서는 loss 함수에 편향값 $b$를 추가하였다.

이 $b$는 학습되는 매개변수로, 초기에 negative 예측에 유리하도록 음의 값으로 초기화한다

$b=-10$으로 설정

동시에 온도 파라미터 $t$는 처음부터 다소 큰 값에서 시작하도록 하여 모델이 초기에 과도한 보정(over-correction)을 하지 않도록 하였다 .

$t=\exp(t’)$이고 $t’$의 초기값을 10으로 설정

이렇게 하면 처음에는 모델이 모든 pair을 negative으로 쉽게 예측하도록 편향되어 시작하므로, 학습 초반에 negative 샘플들의 영향력을 줄이고 positive pair 학습에 집중할 수 있다.

제안한 SigLIP loss의 구현은 매우 간단하다. 논문에서 제공하는 의사 코드(Algorithm 1)를 보면, 불과 몇 줄만으로 loss 계산을 나타낼 수 있다 . 아래는 SigLIP loss 계산을 위한 의사 코드이다.

1
2
3
4
5
6
7
8
9
10
11

# img_emb: 이미지 모델이 출력한 이미지 임베딩 [n, dim]
# txt_emb: 텍스트 모델이 출력한 텍스트 임베딩 [n, dim]
# t_prime, b: 학습되는 로그 온도(t)와 바이어스(b) 변수
# n: 배치 크기 (positive pair 개수)

t = exp(t_prime)                     # 온도 파라미터 t (초기값 exp(10))
z_img = l2_normalize(img_emb)        # 이미지 임베딩 L2 정규화
z_txt = l2_normalize(txt_emb)        # 텍스트 임베딩 L2 정규화
logits = dot(z_img, z_txt.T) * t + b # 유사도 행렬에 온도 t 적용 후 바이어스 b 추가
labels = 2 * eye(n) - ones(n)        # 레이블 행렬: 대각선=1(정답), 나머지
loss = - sum(log_sigmoid(labels * logits)) / n  # 모든 pair에 대한 log-sigmoid loss 평균

위 의사 코드는 논문에 제시된 Algorithm 1과 동일한 내용으로, SigLIP loss의 계산 절차를 구체화한 것이다.

  • 먼저 이미지 임베딩 img_emb와 텍스트 임베딩 txt_emb를 단위 벡터로 L2 normalize

  • 내적을 취해 logits 유사도 행렬을 계산

    • $t = \exp(t^{\prime})$는 학습된 $t’$로부터 온도 스칼라 $t$를 얻는 부분이며, + b는 앞서 언급한 편향값을 더해주는 부분이다.
    • 이렇게 구해진 logits 행렬은 크기가 $n\times n$인 유사도 스코어 행렬이며
      • 원소 $\text{logits}\;[i,j] = t \cdot \langle x_i, y_j\rangle + b$

  • labels 행렬은 대각선에 1, 비대각선에 -1 값을 할당

    • 이는 $z_{ij}$에 해당하며 각 위치가 정답 pair인지 여부를 나타낸다.

  • 마지막 줄에서 labels * logits는 각 유사도 스코어에 해당 pair의 레이블을 곱해 부호를 뒤집는 연산

    • 이 값을 log_sigmoid에 넣으면, 실제로 정답 pair일 때는 $\log(\sigma(s_{ij}))$, negative pair일 때는 $\log(\sigma(-s_{ij})) = \log(1-\sigma(s_{ij}))$에 해당한다 .

      즉 한 줄로 모든 pair의 로그-sigmoid 값을 계산하는 트릭이다.

  • 마지막으로 그 값을 합산해 $-1$을 곱하고 $n$으로 나누어 평균을 취하면 SigLIP의 최종 loss 값 $L_{\text{sigmoid}}$를 얻는다 .

구현이 간결할 뿐 아니라 각 pair별 연산은 병렬로 수행될 수 있어 매우 효율적이다.

softmax 대비 sigmoid loss의 장점은 특히 분산 학습 환경에서 빛을 발한다.

기존 대규모 배치의 contrastive 학습은 데이터 병렬화 시 각 장치의 임베딩을 모두 모아 한꺼번에 계산해야 하므로, 전노드 올갯터(all-gather) 통신과 $|B| \times |B|$ 크기의 유사도 행렬 메모리가 필요했다.

그러나 SigLIP에서는 pair별 loss 계산이 상호 독립이라는 점을 활용해, 배치를 나눠서 부분적으로 loss를 누적하는 “청크(chunk) 단위 계산” 기법을 적용할 수 있다 .

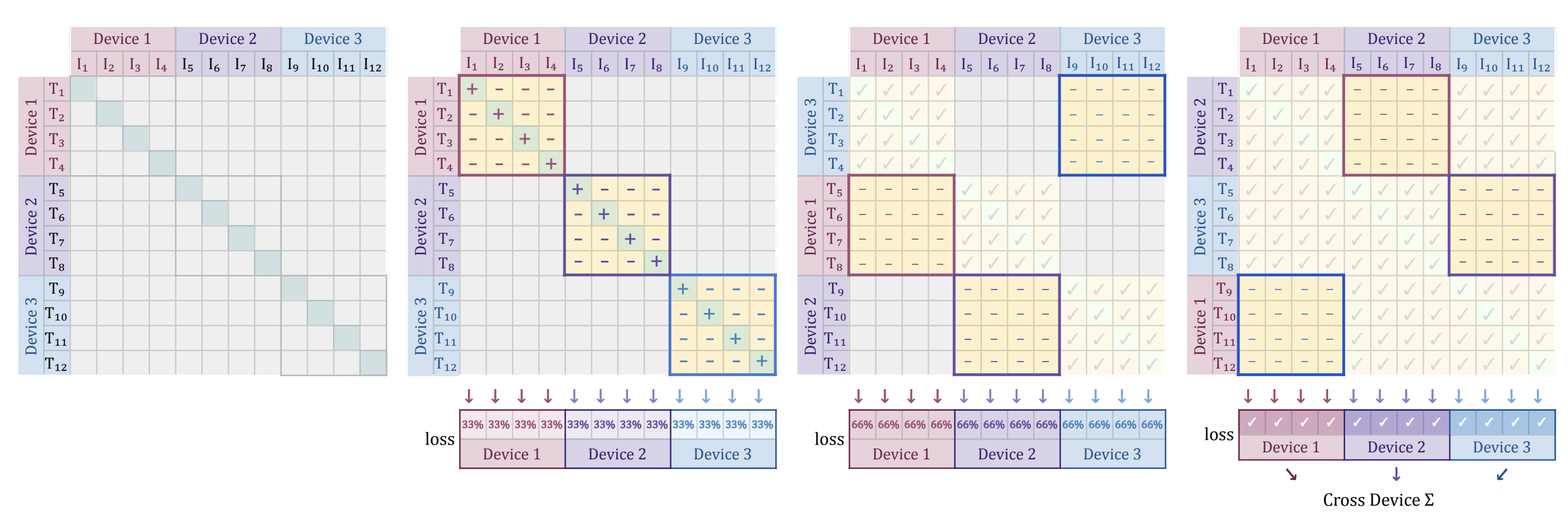
Efficient “chunked” implementation

스크린샷 2025-09-02 오후 5.09.18

3개의 device에 배치 전체(예: 12개 이미지-텍스트 pair)를 분산시켜 효율적으로 loss를 계산하는 방법을 도식화한 그림

우선 각 장치는 자기에게 할당된 데이터(예: 이미지 4개와 텍스트 4개)에 대해서만 부분 loss을 계산한다.

구체적으로,

  1. 자기 장치의 이미지 4개와 텍스트 4개로 구성된 $4\times4$ 유사도 부분행렬에 대해 SigLIP loss(정답 pair 4개 및 일부 negative pair들)을 산출

  2. 장치 간 통신 단계에서 각 장치는 자신의 텍스트 임베딩 4개를 이웃 장치로 전달

  3. 전달받은 다른 장치의 텍스트들과 자신의 이미지들을 짝지어 새로운 negative pair loss를 추가로 계산한 뒤, 이전 단계의 loss 값에 이를 누적

    • 예를 들어, 장치 1이 처음에 (이미지 1–4, 텍스트 1–4)의 loss를 구했다면, 다음에는 이웃한 장치 2로부터 텍스트 5–8을 받아 (이미지 1–4, 텍스트 5–8)의 negative pair loss를 구해 누적

  4. 이 과정을 장치들이 원래 상대편의 텍스트를 모두 한 번씩 받을 때까지 반복

    • 최종적으로 배치 내 존재하는 모든 이미지-텍스트 pair에 대한 loss를 정확히 한 번씩 계산

      중요한 점은 어느 시점에도 각 장치가 다루는 유사도 행렬 청크의 크기가 $b\times b$ (여기서는 4×4 노란색 블록)

    • 덕분에 모든 임베딩을 모으는 연산을 피하면서도, 각 장치 메모리에는 한 번에 큰 행렬을 올려두지 않고도 정확한 전체 loss을 산출 가능

이러한 청크 분산 계산은 sigmoid loss의 독립성 덕분에 가능하며, 결과적으로 동일한 배치 크기에서도 메모리 사용량을 크게 줄이고 통신 대기 시간을 숨겨 학습 효율과 안정성을 높여준다.

Result

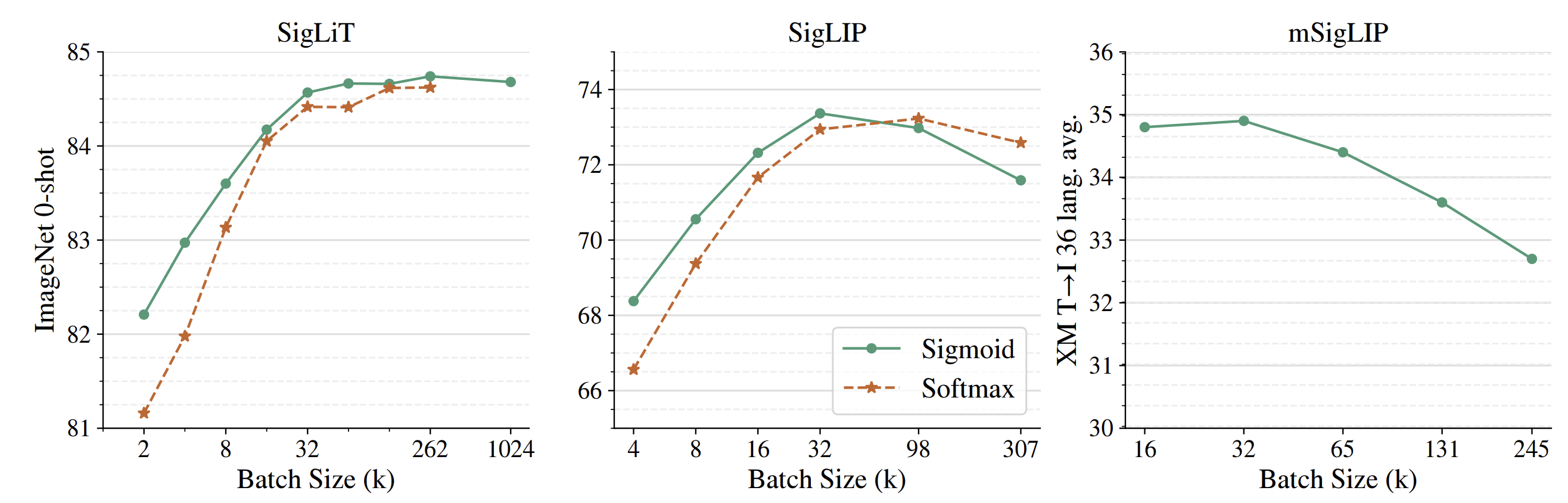
스크린샷 2025-09-02 오후 5.20.22

사전학습 배치 크기를 달리하며 ImageNet zero-shot 분류 정확도(y축)를 평가한 결과

배치 크기 변화에 따른 성능 실험을 통해 SigLIP의 핵심 목표였던 “작은 배치에서도 성능 향상”과 “큰 배치에 대한 유연성”이 확인되었다.

실선은 sigmoid loss로 학습한 모델이고 점선은 동일 조건에서 CLIP(softmax loss)으로 학습한 모델이다.

  • 왼쪽 : SigLiT 설정 (이미지 인코더는 사전학습 모델로 고정, 텍스트 인코더만 학습)
  • 가운데 : 일반 SigLIP (이미지·텍스트 모두 처음부터 학습)
  • 오른쪽 : 다중언어 SigLIP(mSigLIP)으로 100개 언어를 포함한 멀티모달 학습

전반적으로 배치 크기가 작을수록 SigLIP가 CLIP보다 높은 성능을 보였고, 배치 크기를 키워나가면 둘 다 성능이 향상되다가 약 32k 배치에서 성능이 포화되는 양상을 보였다 .

특히 많은 선행 연구들이 배치 크기가 클수록 성능이 계속 향상된다고 가정해 왔지만, 본 실험 결과 32k 이상 초대형 배치에서는 성능 개선이 크지 않거나 오히려 감소하는 경향까지 관찰

이러한 트렌드는 SigLiT의 경우에도 동일하여, 이미지 타워를 고정했을 때도 작은 배치에서는 sigmoid loss이 우월하고 큰 배치에서는 모두 비슷해지는 양상을 보였다 .

mSigLIP 실험의 경우에도 36개 언어 pair retreival 평가에서 32k 배치 정도로 이미 충분하며, 그 이상 배치는 오히려 성능이 떨어지는 결과를 보였다 .

요약하면, SigLIP는 작은 데이터셋/배치로도 좋은 성능을 내기에 유리하며, 극단적으로 큰 배치에 의존할 필요가 없음을 실증한 것이다.

이는 자원이 한정된 연구자들도 멀티모달 모델을 효율적으로 훈련할 수 있음을 시사한다.

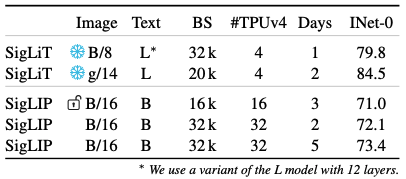
SigLiT with four TPU-v4 chips

스크린샷 2025-09-02 오후 5.09.18

SigLIP의 이러한 효율성은 제한된 하드웨어 자원 시나리오에서도 두드러졌다. 위 표는 적은 수의 TPU로 짧은 기간 학습하여 얻은 모델 성능을 보여준다.

예를 들어, 공개된 ViT-B/16 모델을 이미지 타워로 고정한 SigLiT 설정에서, 불과 4개의 TPUv4 칩으로 24시간 학습하여 ImageNet zero-shot 79.7%의 높은 정확도를 달성하였다.

이는 동일 데이터셋을 처음부터 학습한 CLIP Baseline의 71%대 성능을 크게 상회하는 결과이다.

나아가 이미지 타워를 더 큰 ViT-g/14로 확장하고 동일한 4개 TPUv4로 2일간 학습하여 84.5%의 정확도를 얻었는데 , 이는 OpenAI CLIP 모델이 달성한 84.2% 수준을 뛰어넘는 성능이다.

주목할 점은, CLIP 모델이 이와 비슷한 성능을 얻기 위해 2500 TPUv3-일에 달하는 막대한 연산량을 투입한 데 비해, SigLIP은 32 TPUv4로 단 2일 만에 72.1%에 도달하는 등 훨씬 적은 비용으로 비슷한 정확도를 얻을 수 있었다는 것이다.

이러한 비교는 SigLIP loss이 학습 비용을 획기적으로 절감하면서도 경쟁력 있는 성능을 낼 수 있음을 잘 보여준다.

실제 저자들은 “더 적은 칩으로 더 큰 배치 학습이 가능해졌다”고 언급하며 , 자원 제약이 있는 환경에서 SigLIP의 실용적 가치를 강조했다.

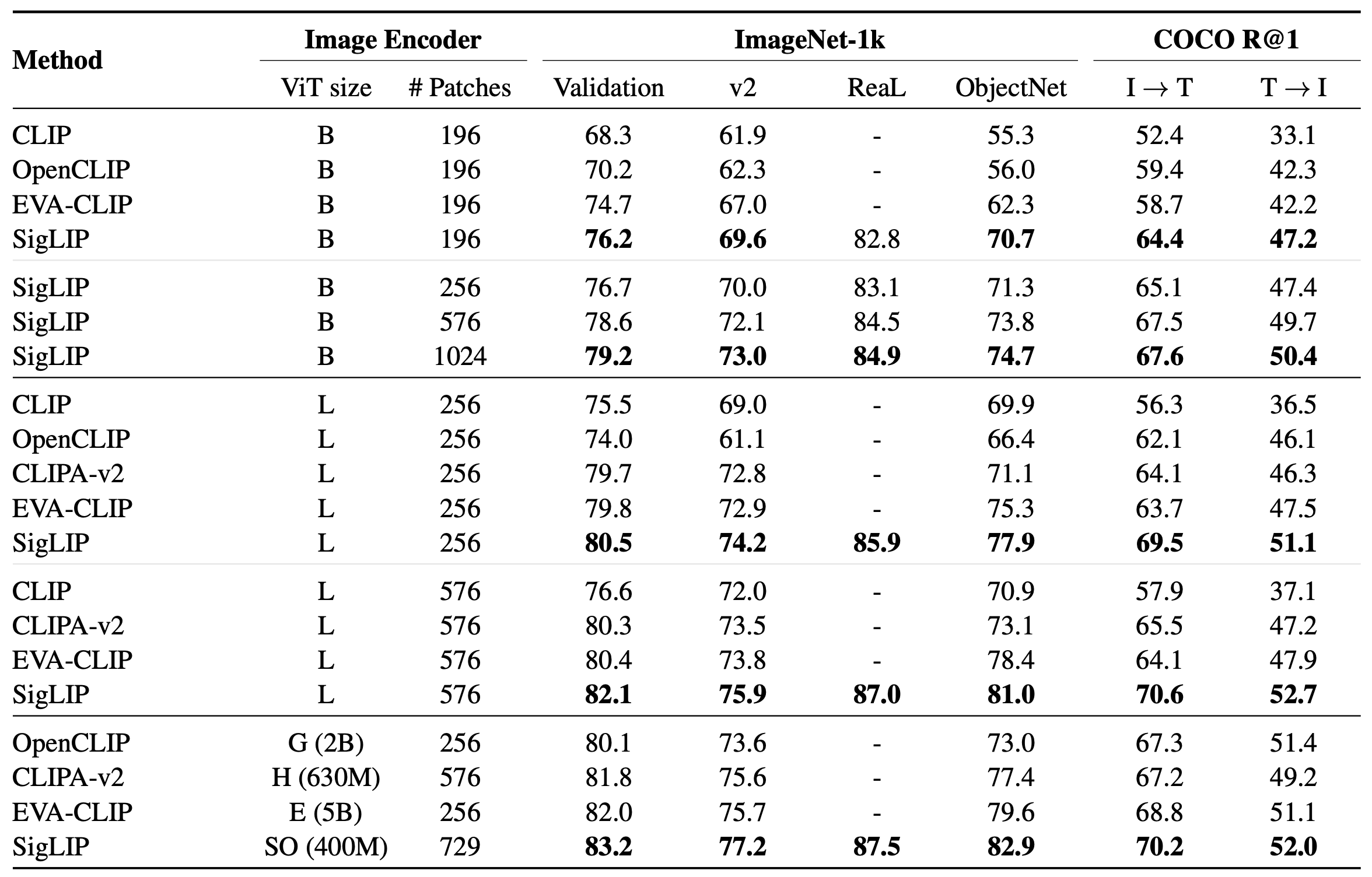
스크린샷 2025-09-02 오후 5.51.00

모델 성능 지표 면에서도 SigLIP는 기존 방법들을 뛰어넘는 결과를 얻었다.

저자들은 학습된 모델을 다양한 벤치마크에 대해 평가하였는데, 위에 요약된 바와 같이 SigLIP로 학습한 모델이 OpenCLIP, CLIP 등 기존 공개 모델들보다 높은 정확도를 보였다 .

예를 들어 ImageNet zero-shot 분류, ObjectNet 등 이미지 분류 작업뿐 아니라 MS-COCO 이미지-텍스트 retreival 작업에서도 SigLIP 모델이 유의미한 성능 향상을 달성하였다 .

이는 SigLIP가 효율성 향상뿐만 아니라 최종 모델의 품질 측면에서도 장점을 가짐을 입증한다. 더욱이 SigLIP는 학습 데이터의 노이즈에 대해서도 강인한 특성을 보였다.

스크린샷 2025-09-02 오후 5.53.12

웹에서 수집한 이미지-텍스트 데이터에는 오타나 잘못 연결된 pair 등 라벨 노이즈(label noise)가 존재할 수 있다.

이를 정량적으로 평가하기 위해, 논문에서는 학습 데이터에 인위적으로 노이즈를 첨가하여 SigLIP과 CLIP의 강인성을 실험하였다.

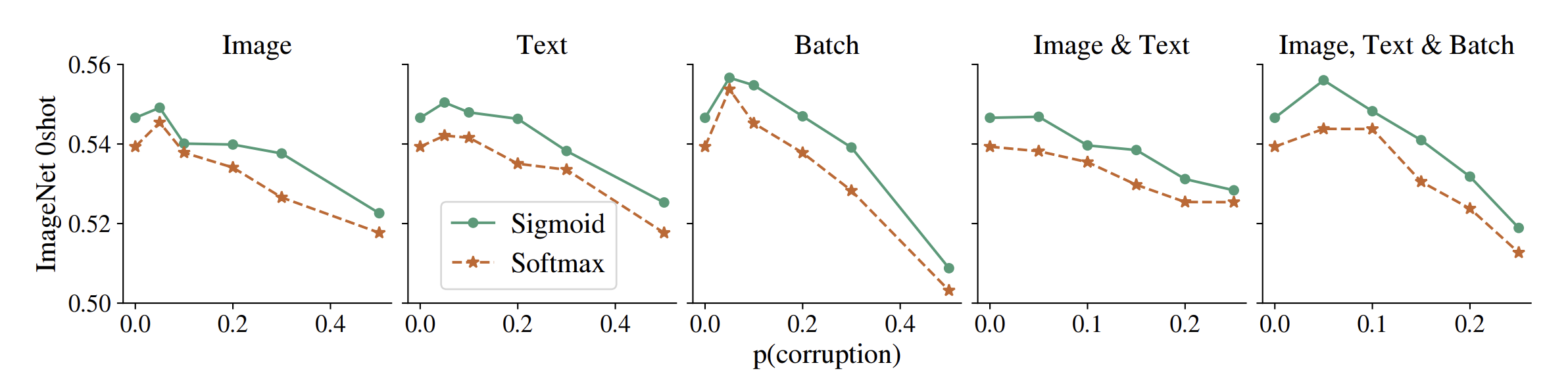
예를 들어 일정 확률로 이미지를 무작위 노이즈 이미지로 바꾸거나, 텍스트를 랜덤 문장으로 대치하거나, 배치 내 이미지-텍스트 짝의 대응을 섞는 등의 다섯 가지 노이즈 시나리오를 적용하였다.

위 그래프는 이러한 다양한 노이즈 수준에 대해 SigLIP(초록색)과 CLIP(주황색) 모델의 성능 변화를 비교한 것이다.

결과는 일관적이었다: 노이즈가 심해질수록 SigLIP(sigmoid loss)로 학습한 모델이 대응되는 softmax 모델보다 높은 성능을 유지하는 것이 확인되었다 .

예를 들어 이미지의 일부를 무작위로 치환하거나 텍스트 토큰을 무작위 재배열하는 등 어떤 형태의 노이즈를 넣어도, SigLIP 모델은 노이즈 비율 $p$가 증가하는 상황에서 상대적으로 완만하게 성능이 감소하며 끝내 CLIP 모델보다 우수한 정확도를 보였다 .

이러한 경향은 실험된 모든 노이즈 종류에 걸쳐 나타났으며, 레이블 오류에 대한 sigmoid loss의 견고함을 보여주는 결과라 할 수 있다 .

다만 저자들도 이 현상의 원인을 추가로 분석하지는 않았는데, sigmoid loss의 개별 pair 학습이 노이즈 영향 분산에 유리한 것으로 추측된다.

Conclusion

Sigmoid loss를 활용한 언어-이미지 사전학습(SigLIP)은 loss 함수 설계를 통해 대규모 멀티모달 모델 학습의 효율과 성능을 모두 향상시킨 연구이다. 본 논문의 실험을 통해 얻은 주요한 내용을 정리하면 다음과 같다.

  • sigmoid 기반 loss로 배치 전역 정규화를 제거함으로써 메모리 효율을 크게 높이고, 분산 학습 시에도 대규모 통신 병목 없이 loss 계산이 가능하게 되었다 .
  • 작은 배치나 제한된 하드웨어 환경에서도 softmax 대비 높은 성능을 유지하여, 적은 비용으로도 대규모 모델 학습이 가능함을 보였다 .
  • 학습된 모델은 ImageNet 분류, MSCOCO retreival 등 다양한 벤치마크 테스트에서 기존 대비 더 높은 정확도를 달성하며, SigLIP의 효용을 입증했다 .
  • 학습 데이터에 노이즈가 존재할 경우에도 SigLIP 모델이 대응되는 CLIP 대비 일관되게 우수한 성능을 보이며, 레이블 오류에 대한 견고성이 향상되었다 .

SigLIP은 이처럼 학습 비용 절감과 성능 향상 두 마리 토끼를 잡은 흥미로운 사례로서, 멀티모달 대규모 모델을 보다 효율적으로 훈련하려는 향후 연구에 중요한 기반이 될 것으로 기대된다. 저자들 역시 연구를 통해 얻은 모델과 코드를 공개하면서, 이러한 접근이 멀티모달 사전학습의 품질과 효율을 개선하는 향후 연구들을 촉발하기를 희망하고 있다 .

Limitations

  • 대형 배치에서의 학습 불안정성: 배치가 커질수록 loss 곡선이 불안정해지고 gradient spike가 발생하여, Adam/AdaFactor의 $β_2$를 기본 0.999에서 0.95로 낮춰야 안정화된다(모든 실험에 0.95 적용). 즉, 레시피 민감도가 존재한다.
  • 배치 스케일링의 한계(포화/역효과): 배치 크기를 크게 키워도 약 32k에서 성능 포화가 관찰되고, 다국어(mSigLIP) 설정에서는 32k 이상에서 오히려 성능이 악화되기도 한다. 무한정 배치 스케일링으로 성능을 올리기 어렵다.
  • 음성/양성 쌍 불균형 처리의 난점: 시그모이드 손실은 쌍별 로지스틱으로 음성이 압도적으로 많은 구조다. 단순 랜덤 마스킹은 성능을 해치고, easy negative 유지도 효과가 없으며, hard negative 마이닝이 유망하지만 효율적 설계가 쉽지 않다(비보 trivial).
  • 프리트레인 비전 타워 미세조정의 민감성: 공개 사전학습 비전 타워를 그대로 미세조정하면 성능이 잘 안 나오며, 프리트레인 가중치에는 weight decay를 끄는 등 특별한 레시피 조정이 필요했다(기본 설정에선 10-shot 선형평가에서도 간신히 개선).
  • 여전히 큰 자원 요구(From-scratch): CLIP류를 처음부터 학습하는 것은 여전히 자원 집약적이다. SigLIP로 칩 수를 줄이고 배치를 키우는 이점이 있으나, 근본적으로 대규모 사전학습의 연산·데이터 비용 문제를 완전히 제거하지는 못한다.
  • 하이퍼파라미터/초기화 의존성: 시그모이드 손실의 bias 항(b)과 그 초기값(예: −10), 그리고 온도(learnable $t$) 설정이 성능에 일관된 영향을 미치며, 적절한 초기화가 필요하다.
Paper Review, Multi Modal, ICCV2023
ICCV Multi-modal Google VLM CLIP DeepMind