[Paper Review] Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

[논문 리뷰] Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

Keyu Tian, Yi Jiang, Zehuan Yuan, Bingyue Peng, Liwei Wang

NeurIPS 2024 Oral (recieved Best Paper Award)

[Arxiv]

최신 LLM에서 성능을 보여주고있는 Autoregressive 방식을 이미지 생성에 적용한 논문

Background

Autoregressive Modeling via Next-Token Prediction

시퀀스의 다음 요소를 순차적으로 예측(next token prediction)하는 방법이다.

정의: autoregressive 모델은 시퀀스의 joint 확률을 인접한 이전 항들만의 함수로 분해한다.

시퀀스 $x = (x_1, x_2, \dots, x_T)$가 주어질 때, next-token autoregressive 가정에 따르면 현재 token의 확률분포는 이전까지의 prefix $(x_1,\dots,x_{t-1})$에만 의존한다.

이에 따라 시퀀스의 전체 확률은 chain rule로 인해 다음과 같이 인수분해된다:

\[p(x_1, x_2, \dots, x_T) = \prod_{t=1}^{T} p(x_t \mid x_1, x_2, \dots, x_{t-1})\]

여기서 $x_t \in [V]$는 정수형 token (코드북 크기 $V$ 내)이며, $p_\theta(x_t \mid x_{<t})$를 최대화하도록 모델 파라미터 $\theta$를 학습시킨다 . 이 Next token prediction으로 학습된 $p_\theta$는 새로운 prefix에 대해 다음 token을 샘플링함으로써 new 시퀀스를 생성할 수 있다.

특성은 다음과 같다

• 스케일링 법칙

  • autoregressive 언어모델의 테스트 loss $L$이 모델 파라미터 수 $N$ 등에 대해 거의 거듭제곱 관계로 감소함이 관찰

  • $L(N)\propto N^{-\alpha}$ 형태로 모델/데이터/연산량을 스케일 업할수록 성능이 향상

    작은 모델로 큰 모델의 성능을 예측해 자원을 효율 배분 가능

    모델 성능이 크기에 비례해 꾸준히 향상됨이 LLM 성공의 핵심 요인

• Zero-shot Generalization

  • Zero-shot 학습 : 훈련 때 명시적으로 학습하지 않은 task를 입력 프롬프트만으로 수행하는 능력

  • GPT-3 등의 거대 LLM들은 방대한 unsupervised learning을 통해 새로운 질의 형식이나 task에도 바로 답하거나 몇 샷 예제로 즉석 적응하는 뛰어난 범용성을 보임

    in-context learning

Tokenization

이미지를 다루려면 continuous한 2D 픽셀을 discrete token 시퀀스로 변환해야 한다 . 일반적으로 VQ-AutoEncoder $E, D, Q$를 사용하여 이미지 $i_m$를 latent feature map $f = E(im)$로 인코딩한 뒤 (예: $f\in\mathbb{R}^{h\times w \times C}$), 양자화 $Q$를 통해 $f$의 각 위치 $(i,j)$를 코드북 $Z$의 항목으로 치환하는 token map $q$로 변환한다:

\[f = E(im), \qquad q = Q(f)\]

여기서 $q(i,j) \in [V]$는 코드북 인덱스이다. 양자화는 보통 $f$의 각 벡터 $f_{(i,j)}$와 가장 가까운 코드북 벡터를 찾는 것으로 구현된다:

\[q(i,j) ;=; \underset{v\in [V]}{\arg\min} ;\|\text{lookup}(Z, v)-f_{(i,j)}\|_2 ,\in [V]\]

여기서 $\text{lookup}(Z, v)$는 코드북 $Z$에서 인덱스 $v$에 해당하는 벡터를 가져오는 연산이다. $q$를 얻은 후, decoder $D$를 통해 $\hat f = \text{lookup}(Z, q)$로 복원한 feature으로부터 재구성 이미지 $\hat{im} = D(\hat f)$을 얻을 수 있다 (식 (4)). VQ-VAE는 원본 $im$과 재구성 $\hat{im}$ 사이의 차이를 최소화하도록 학습되며, 일반적으로 다중 loss을 사용한다:

\[\hat{f} = \text{lookup}(Z, q), \qquad \hat{im} = D(\hat{f})\] \[L = \|im - \hat{im}\|^2 + \|f - \hat{f}\|^2 + \lambda_\text{P} L_\text{P}(\hat{im}) + \lambda_\text{G} L_\text{G}(\hat{im}).\]

위 loss 식에서 첫 두 항은 픽셀 L2 재구성 오류와 양자화 embedding 오차이고, $L_P$는 지각 loss(perceptual loss, 예: LPIPS ), $L_G$는 판별자 loss(generative adversarial loss)이며 $\lambda_P, \lambda_G$는 가중치이다.

VQ-VAE 학습 완료 후, encoder $E$와 양자화기 $Q$를 사용해 대량의 이미지들을 token 시퀀스로 변환하고, 이를 autoregressive 모델의 훈련 데이터로 삼는다 .

1D 시퀀스로의 변환

token map $q \in [V]^{h\times w}$은 2D에 자연스러운 순서가 없으므로, 1D 시퀀스 $x = (x_1,\dots,x_{h\cdot w})$로 전개 순서를 정의해야 한다.

선행 연구들은 일반적으로 행 우선 래스터 순서(row-major raster-scan)로 펼치거나, 특수한 순서(spiral, z-curve 등)를 사용하였다 .

일단 token을 나열하고 나면, Next token prediction에 따라 표준 cross entropy loss로 Transformer $p_\theta(x_t \mid x_{<t})$를 학습시킬 수 있다 . 이것이 기존 autoregressive(AR) 이미지 생성 모델의 기본 훈련 과정이다.

위 tokenization 및 1D 전개 전략은 다음 token autoregressive 학습을 가능케 했지만, 몇 가지 중대한 한계가 있다:

• autoregressive 가정 위배

  • VQ-VAE encoder가 출력하는 featuremap $f$의 공간적 벡터들은 서로 상호의존적
  • 양자화 후 얻은 token 시퀀스 $(x_1,\dots,x_{h\cdot w})$ 안에는 양방향 상관관계가 존재하며, 각 token이 앞부분만 참조한다는 autoregressive 모델의 전제에 어긋난다.

• 제한된 생성 방향성

  • 1D 단방향 생성은 일부 영역만 주어졌을 때 다른 부분 채우기 등의 zero-shot 작업에 부적합

  • 이미지 하반부를 주고 상반부를 생성하는 경우, 래스터 순서에서는 상반부 token이 뒤에 나오므로 이러한 역방향 생성이 불가능

    이는 양방향 문맥이 필요한 작업에서 AR 모델이 일반화하지 못함을 의미

• 공간 구조의 loss

  • token을 늘어놓으면서 원래 공간적 이웃 관계가 단절

  • 인접 픽셀들은 강하게 상관되어 있지만, 1D 시퀀스에서 이들 사이에는 수많은 다른 token이 끼어들고 단방향 제약까지 있어 local pattern 학습이 어려워진다.

    이는 생성 결과의 세밀한 구조 품질에 악영향을 준다.

• 낮은 효율성

  • $n\times n$ 해상도의 이미지는 $n^2$개의 token을 가지는데, 이를 순차 생성하면 $O(n^2)$ 단계가 필요

  • Transformer의 매 단계 복잡도도 $O(n^2)$이어서 총 $O(n^6)$의 연산

    → 해상도가 커지면 계산량이 급격히 증가하여 실용적 생성이 어렵다.

Image generation model

Autoregressive (AR) 모델

초창기 PixelRNN/CNN 등은 픽셀 단위로 이미지를 순차 생성하였고 , 이후 VQ-VAE로 latent space에서 token을 생성하는 VQGAN , DALL-E 등으로 발전했다.

이들 모델은 이미지 token을 1D 시퀀스로 나열하여 GPT-2 스타일 Transformer로 다음 token을 예측한다 .

VQVAE-2 , RQ-Transformer 등은 latent token map을 계층적으로 쌓거나 다단계로 생성했지만 여전히 최종적으로는 1D 순차 생성에 의존했다.

Parti 는 ViT-VQGAN 기반으로 Transformer를 20억 파라미터까지 키워 텍스트-이미지 합성 성능을 높였다.

하지만 이런 AR 모델은 token 수가 많아 생성이 느리고, 모델을 키워도 diffusion model만큼 성능이 높지 않다는 한계가 있었다.

Mask prediction (BERT-스타일) 모델

MaskGIT 은 이미지 VQ token을 한꺼번에 예측하는 masked 생성 접근으로, 반복적으로 일부 mask를 채워넣어 이미지를 완성한다 (BERT와 유사).

이 방식은 8~16회의 병렬 예측 단계로 이미지 생성을 가속했고, MagVIT 은 이를 비디오로 확장, MUSE는 파라미터 30억까지 스케일 업하였다 .

Diffusion model

노이즈를 단계적으로 제거하며 이미지를 생성하는 접근으로, 학습 및 샘플링 기법 발전 과 Guidance 기법 등을 통해 현재 이미지 합성의 대표적 방법이 되었다.

특히 Diffusion Transformer (DiT)는 U-Net 대신 Transformer로 diffusion 과정을 구현한 것으로 Stable Diffusion 3.0, SORA 등 최신 시스템의 기반이 되었다 .

diffusion model은 고품질 이미지를 생성하지만 수백 step inference가 필요해 느리다는 단점이 있다 .

본 논문의 VAR 모델은 autoregressive Transformer로 diffusion model 수준의 성능을 내면서도 추론 단계를 극적으로 줄여 양자의 강점을 결합하고자 한다.

Introduction

이 논문은 Visual AutoRegressive 모델링(VAR)을 제안한다.

VAR는 이미지 autoregressive 학습을 next-token prediction 대신 next-scale prediction 방식으로 재정의하여, 저해상도부터 고해상도로 점진적으로 이미지를 생성하는 새로운 패러다임이다.

이를 통해 기존 1D 순차 token 생성의 한계를 극복하고 학습 효율과 일반화 성능을 크게 향상시켰다.

VAR는 ImageNet 이미지 생성에서 최초로 diffusion model을 능가하는 성능을 내었고, 파워-law 스케일링 법칙 및 zero-shot 일반화 능력까지 보여주었다

Goal

새로운 다중-스케일 autoregressive 생성 framwork를 개발하여, 기존 AR 이미지 생성 모델의 성능 한계를 극복하고 diffusion model 수준의 고품질 이미지를 효율적으로 생성하도록 하는 것.

VAR를 통해 GPT 계열 AR 모델이 diffusion Transformer를 능가하는 첫 사례를 만드는 것을 목표로 한다.

Motivation

기존 시각적 AR 모델의 한계가 분명하다.

1. vision token을 1D로 펼치면 autoregressive의 feature인 각 token은 이전 token들에만 의존한다는 점이 성립 X
2. 시퀀스 종속 때문에 부분 이미지 채우기 등의 zero-shot 작업이 불가능
3. token 간 공간적 인접성이 깨져 구조적 일관성이 하락
4. token 개수가 방대해 추론 비용이 $O(n^6)$ 수준으로 매우 방대

이로 인해 AR 모델은 diffusion model보다 학습/추론이 비효율적이고 성능도 낮았는데, 이러한 비효율과 성능 열세를 극복하고자 한다.

Contribution

1. next-scale prediction이라는 새로운 다중-스케일 autoregressive 생성 패러다임을 제시

   컴퓨터 vision 분야 autoregressive 알고리즘 설계에 대한 새로운 관점을 제공

2. VAR 모델을 통해 스케일링 법칙과 zero-shot 일반화가 Vision generation 모델에서도 나타남을 처음으로 실증

LLM의 흥미로운 속성을 시각 모델에서도 구현했음을 입증

1. GPT 계열 AR 모델이 처음으로 강력한 diffusion model을 능가하도록 만들어, 이미지 합성 성능·다양성, 데이터 효율, 추론 속도 면에서 SOTA을 달성

VAR tokenizer와 autoregressive 모델 학습 파이프라인 등 포괄적인 오픈소스 코드가 공개되어있다.

Method

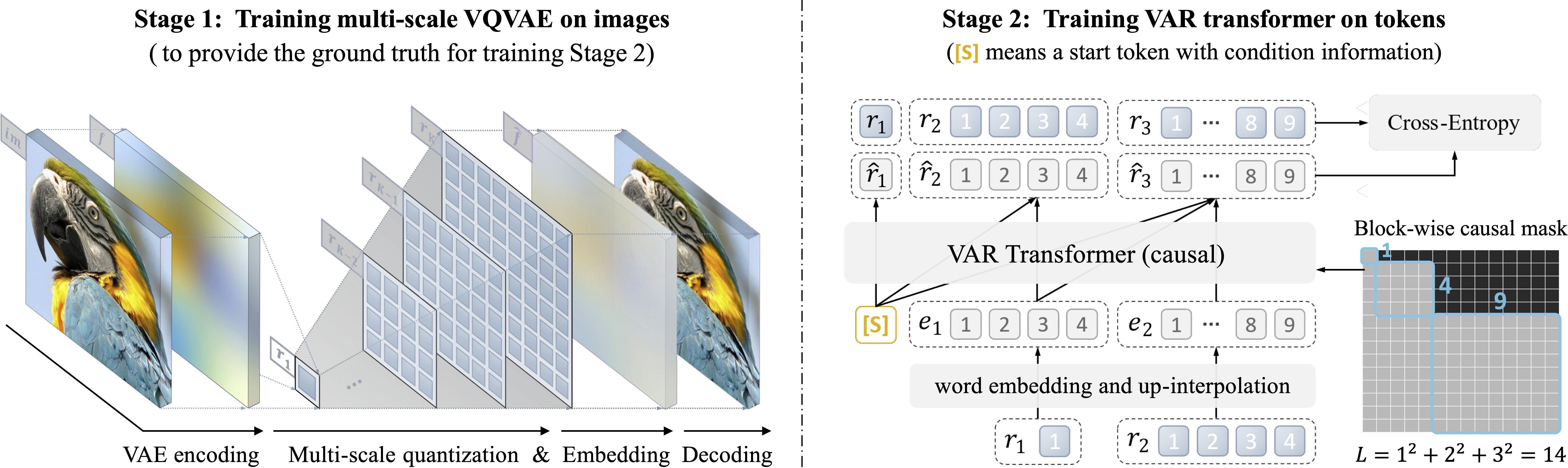
본 연구의 방법론은 2단계로 구성된다.

1. 다중-스케일 VQ-VAE tokenizer를 학습하여 이미지를 여러 해상도의 discrete token map으로 변환
2. 이러한 다중 token map을 Next-scale prediction 방식의 Transformer로 학습하여, 낮은 해상도부터 순차적으로 높은 해상도의 token map을 생성

Stage 1 : Multi-scale tokenization

앞서 VAR의 전제는 “각 $r_k$는 prefix $r_{<k}$로부터만 결정”되는 것이다. 이를 만족시키려면 tokenization 과정에서 잔여(residual) 정보 분리가 필요하다.

논문에서는 새로운 다중-스케일 VQ-VAE를 고안하여 이미지로부터 $K$개의 token map $R=(r_1,\dots,r_K)$을 추출한다 .

알고리즘 1(Encoding)과 2(Decoding)은 구체 절차를 제시하는데, 요약하면 다음과 같다:

• Encoding

  1. Encoder $E$로 입력 이미지에서 feature map $f$를 추출

  2. 그리고 $k=1$부터 $K$까지 반복:

     1. 현재 feature $f$를 해상도 $(h_k, w_k)$로 downsampling (양자화 전 보간).
     2. 양자화 $Q$로 token map $r_k$를 얻는다.
     3. 큐(queue)에 $r_k$를 저장해 두고, 코드북을 조회하여 embedding map $z_k = \text{lookup}(Z, r_k)$로 변환
     4. $z_k$를 최종 해상도 $(h_K, w_K)$까지 upsampling하여 $\tilde{z}_k$로 만든다.
     5. 보조 합성기(convolution) $\phi_k$로 $\tilde{z}_k$를 다시 이미지 feature 차원으로
     6. 현재 feature map에서 뺌: $f := f - \phi_k(\tilde{z}_k)$.
  • 이렇게 하면 $r_k$가 현재 feature $f$에서 제거된 정보를 나타내므로, 다음 스케일 $k+1$로 넘어갈 때 $f$에는 잔차만 남는다 . 마지막 $k=K$ 단계 후엔 모든 feature가 제거되고, $R=(r_1,\dots,r_K)$만 남는다.

  위 과정에서 모든 스케일이 공동 코드북 $Z$ (크기 $V$)를 사용하므로, $r_k$의 각 token은 동일한 어휘 공간 $[V]$의 원소이다 .

  이는 다중 스케일 token들이 동일한 embedding 공간에서 representation됨을 의미한다.

  또한 $\phi_k$는 $k$별로 다른 $1\times1$ convolution 계층으로, 해상도 업샘플 후 발생할 수 있는 정보 loss을 보완한다 . ($\phi_k$는 downsampling 후에는 사용 안 함).

• Decoding

  1. 가장 큰 token map $r_K$부터 차례로 pop하여 코드 embedding $z_k = \text{lookup}(Z, r_k)$로 변환
  2. $z_k$를 전체 해상도로 upsampling
  3. 각 스케일의 $\phi_k(z_k)$를 순차적으로 누적합하여 $\hat f = \sum_{k=1}^K \phi_k(\tilde{z}_k)$를 얻는다.
  4. 마지막에 decoder $D(\hat f)$로 이미지 $\hat{im}$을 복원

이는 RQ-Transformer의 residual VQ와 유사한 Residual Quantization 방식을 채택하여, 각 단계가 이전 단계들 prefix로부터만 정보를 받아오도록 구성되었다고 볼 수 있다 .

loss 함수는 복합 loss을 사용하며, OpenImages 데이터셋에서 VQGAN과 동일한 설정으로 tokenizer를 학습하였다 .

이렇게 학습된 VAR tokenizer는 16배 다운샘플 (이미지 해상도의 $1/16$ 크기 latent) 기준으로 코드북 크기 $V=4096$을 사용하며, 파라미터는 $\sim 13.4$M으로 경량이다.

Stage 2 : Visual Autoregressive Modeling via Next-Scale Prediction

VAR는 시퀀스의 token 단위를 새롭게 설정한다.

기존에는 하나의 token(픽셀 혹은 코드)을 한 step으로 생성했다면, VAR에서는 해상도별 token map 전체를 하나의 단위로 취급하여 “다음-스케일”을 생성한다.

구체적으로, 이미지 encoder를 통해 얻은 featuremap $f\in \mathbb{R}^{h\times w \times C}$를 여러 단계의 해상도로 양자화하여 $K$개의 token map $(r_1, r_2, \dots, r_K)$으로 변환한다.

여기서 각 $r_k$는 해상도 $h_k \times w_k$를 가지며, 마지막 $r_K$의 크기가 원본 feature과 동일 ($h_K=h, w_K=w$)이다. VAR의 autoregressive 확률 모형은 다음과 같이 정의된다:

\[p(r_1, r_2, \dots, r_K) ;=; \prod_{k=1}^{K} p!\big(r_k \mid r_1, r_2, \dots, r_{k-1}\big), \tag{6}\]

여기서 Autoregressive 단위 $r_k \in [V]^{h_k \times w_k}$는 해상도 $k$의 전체 token map이며, $r_{<k}=(r_1,\dots,r_{k-1})$는 그보다 작은 스케일들의 token map 시퀀스이다.

$k$번째 생성 단계에서는 token map $r_k$의 모든 token들을 병렬로 한꺼번에 생성한다.

단, $r_k$를 생성할 때는 이전 단계들 $r_{<k}$만 참고하고 아직 생성되지 않은 $r_{>k}$는 보지 않도록 블록 단위의 masking을 적용하여 학습한다.

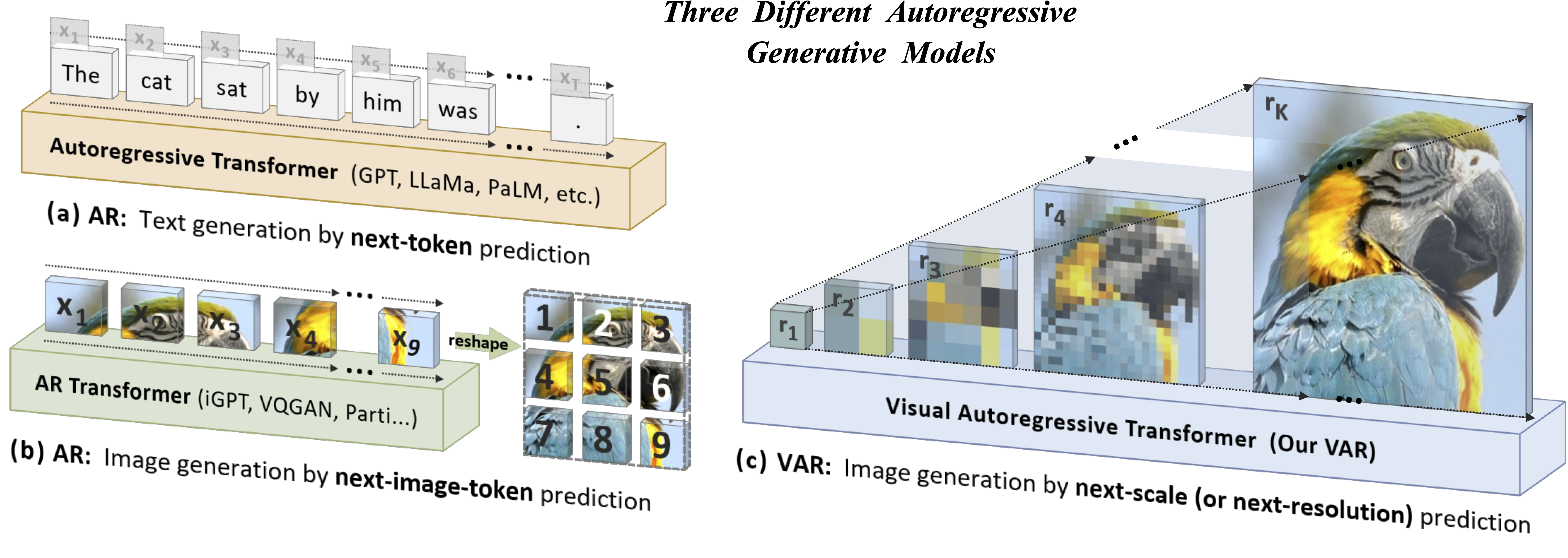
이렇게 다음 스케일 예측 전략으로 이미지를 점진적(조 coarse→fine)으로 만들어가는 것이 VAR(시각적 autoregressive) 모델링의 핵심이다.

(a) 텍스트 AR: 단어 단위 순차 생성, (b) 이미지 AR: token 단위 래스터 순차 생성, (c) VAR: 여러 해상도의 token map을 coarse-to-fine으로 생성 (같은 해상도 token은 병렬 생성)

tokenizer(Stage 1)로 얻은 $K$개의 token map 시퀀스 $R$를 가지고, 이제 (식 (6))의 확률모델을 학습한다.

모델 구조는 GPT-2 스타일의 decoder 전용 Transformer로, VQGAN의 Transformer와 동일한 아키텍처를 사용하였다.

주된 수정 없이도 새로운 paradigm의 효과를 검증하기 위해 AdaLN (Adaptive LayerNorm), q,k 정규화 등 몇 가지만 적용하고 다른 복잡한 트릭(예: RoPE, ALiBi 등)은 사용하지 않았다.

클래스 조건부 생성을 위해 ImageNet 클래스 embedding을 시작 token [s]으로 추가하고 AdaLN의 조건으로도 활용하였다.

학습 시에는 블록별 causal mask를 사용해 $r_k$가 $r_{<k}$까지만 attend하도록 강제하였고 , 추론 시에는 일반 autoregressive 모델처럼 이전 출력 ($r_{<k}$)을 캐싱하여 mask 없이 빠르게 생성한다.

VAR의 coarse-to-fine 생성은 앞서 언급된 한계들을 다음과 같이 개선한다 :

• autoregressive 전제 충족

  • 각 $r_k$는 오직 이전 스케일 $r_{<k}$에만 의존하도록 학습

    각 스케일에서 prefix는 더 작은 해상도 token map들

    • 이는 인간의 시각적 인지나 드로잉 과정이 대략 -> 세부로 이루어지는 자연스러운 순서와 부합
    • encoder feature 사이의 양방향 의존 문제를 해소

  • 다시 말해 작은 스케일의 거친 그림을 그리고 점차 세부를 추가하는 방식으로 autoregressive 진행을 재구성함으로써 모델 가정에 어긋남 없이 학습이 가능

• zero-shot 일반화 가능성

  • 공간적으로 양방향 정보 활용이 부분적으로 가능

  • VAR에서는 이미지를 처음부터 끝까지 한 방향으로 그리는 대신, 처음 단계에서 전체 이미지의 골격($r_1$ 저해상도)를 생성하고 이후 점진적 보완

    • 따라서 일부분이 주어지고 나머지를 생성하는 경우, 주어진 부분은 고해상도 token으로, 그 축소 버전이 이전 스케일들에 포함되어 단서로 활용될 수 있다.

    실제로 저자들은 학습 없이 VAR로 이미지 인페인팅, 아웃페인팅, 편집 등을 수행해보았고, 그 결과 이전 AR에 없던 zero-shot 적응력을 확인

• 공간 구조 보존

  • VAR에서는 token map을 1D로 펼치지 않고 각 해상도에서 원래의 2D 구조를 유지한 채 병렬로 생성
    • 인접 token들 간 상관성을 자연스럽게 학습
  • 다중 해상도 설계로 token 계층 구조를 형성
    • 작은 스케일에서 큰 구조를, 큰 스케일에서 세부를 담당 → 공간적 일관성이 강화

• 효율 향상

  • 한번에 하나씩 $n^2$개의 token을 생성하던 기존과 달리, VAR는 $K$단계만 거치면 모든 token map이 생성
  • $K \approx O(\log n)$이며, 각 단계에서 $r_k$의 $n_k^2$개의 token을 병렬 생성 → 총 생성 복잡도는 $O(n^4)$로 완화
    • 이론적으로 $n^2$배 빠르고, 실측 약 20배 이상 빠르다

모델/학습 세부사항: 다양한 크기의 VAR Transformer를 실험했는데, depth(layer 수) $d$를 1630까지 늘리며 크기를 키웠다. layer 깊이 $d$에 따라 embedding 차원 $w=64d$, 멀티헤드 수 $h=d$ 등 규모를 조절하여 파라미터 수가 $N(d) \approx 73728,d^3$로 증가하도록 설정하였다.

\[N(d) = d \cdot4w^2 + d \cdot8w^2+d\cdot 6w^2 = 18dw^2 = 73728d^3\]

예컨대 $d=30$일 때 약 $2.0$B 파라미터에 달한다.

모델들은 ImageNet-1k 훈련셋으로 학습했으며, 배치 7681024에 learning rate $10^{-4}$ (AdamW, β1=0.9, β2=0.95), 200~350 epochs 정도 훈련하였다 .

이러한 단순 구성에도 불구하고, 다음 절의 실험에서 드러나듯 뛰어난 스케일링과 일반화 성능을 보였다 .

Empirical Results

실험 개요: 저자들은 VAR을 다양한 이미지 생성 benchmark에서 평가하고, 동급 최고 모델들과의 비교, 스케일링 법칙 검증, zero-shot 전이 실험, 모델 구성요소별 영향 등을 분석하였다.

5.1 State-of-the-art Image Generation

Set up: ImageNet 클래스 조건부 이미지 생성 작업에서, 여러 크기의 VAR 모델 (depth 16, 20, 24, 30; 해상도 256×256 및 512×512) 성능을 측정한다.

그리고 동시대 생성 모델들과 성능을 비교한다:

• GAN 기반 (BigGAN, StyleGAN-XL 등)
• diffusion model (ADM, CDM, Latent Diffusion, DiT 등)
• mask 예측 (MaskGIT, RCG)
• 기존 AR (VQGAN, ViT-VQGAN, RQ-Transformer)

등이 포함되었다.

VAR과 VQGAN은 동일한 VQtokenizer (OpenImages 학습) 사용, RQ-Transformer 등은 ImageNet 자체 tokenizer 사용 등의 차이가 있다 .

성능 지표로는

• FID(↓, 낮을수록 좋음)
• Inception Score (IS↑)
• Precision/Recall
• 파라미터 크기
• 1장 생성에 필요한 추론 step 수 및 실시간 속도(VAR 대비 상대시간)

등을 비교한다.

ImageNet 256×256 결과

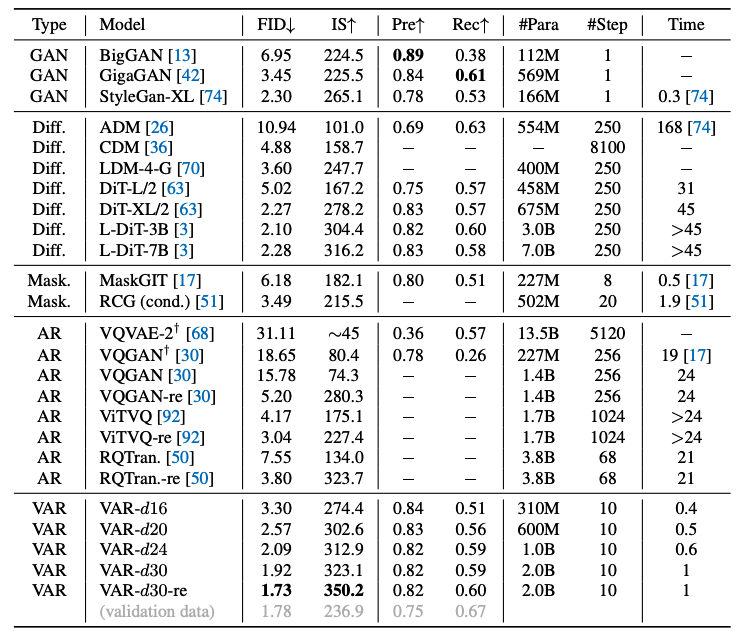
VAR 모델들은 모든 비교 대상 중 최고의 이미지 품질을 보여주었다.

• VAR-d30-re (depth 30 모델에 rejection sampling 적용)
  • FID = 1.73, IS = 350.2
    • 이전 AR 최고였던 VQGAN-re (FID 5.20)나 diffusion 최고인 L-DiT-3B (FID 2.10)보다도 월등히 낮은 FID를 달성
    • IS 또한 350 이상으로 다른 모델들을 크게 앞선다.
  • Precision 0.82, Recall 0.60 수준으로 모드 다양성도 확보

주목할 점은 GPT계 AR 모델이 처음으로 diffusion 기반을 능가했다는 사실로, Diffusion Transformer (DiT) 계열 (최신 Stable Diffusion 3.0의 근간)의 FID/IS를 VAR가 넘어섰다.

또한 VAR는 동일 조건 VQGAN 대비 20배 이상 빠른 추론을 달성하여, 1-step인 GAN 수준의 속도에 근접했다.

예컨대 DiT-XL은 이미지당 250 denoise step(상대속도 45×)이 필요하지만, VAR는 10step만으로 완성

Precision-Recall 측면에서도 VAR는 우수한 정밀도와 다양성의 균형을 보였다 (Prec ~0.83, Rec ~0.59) .

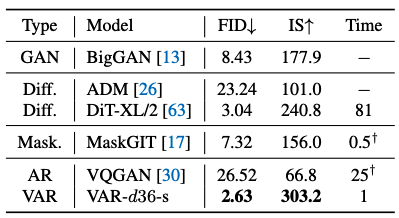
ImageNet 512×512 생성 비교 . VAR는 고해상도에서도 diffusion/기존 AR보다 뛰어난 성능을 유지한다.

512×512 결과도 유사하게, VAR가 FID ~2.6으로 타 모델을 제치며, AR 모델로서 최초로 Diffusion을 앞선 사례를 세웠다 . (다만 512 실험에서는 자원 한계로 AdaLN layer 일부를 공유(-s)하며 36-layer 모델을 사용).

추론 효율

전통 AR 모델은 고해상도로 갈수록 계산량이 급증하여 실용화가 어려웠다.

반면 VAR는 다중 스케일 병렬 생성 덕에 복잡도를 크게 낮추고 실측 속도도 개선하였다.

논문에 따르면 $n^2$개 token 생성에 AR는 $O(n^6)$, VAR는 $O(n^4)$ 시간이 소요된다.

이는 256×256 기준 약 $65k$번 대 $5$번의 autoregressive step 차이다 .

표 1의 Wall-clock 시간 비교에서도, VAR 대비 기존 VQGAN은 19배, ViT-VQGAN은 24배 느려 약 20× 시간 소요되었다.

VAR 20억 모델은 여전히 310M짜리 VQGAN보다 빨랐다. GAN류(1step)은 여전히 가장 빠르지만, VAR는 Transformer 기반 모델 중 거의 유일하게 실시간 생성에 근접한 성능을 보였다.

DiT (Diffusion Transformer) 대비

VAR의 제안 의의 중 하나는, 동일 Transformer 아키텍처 기반인 Diffusion 모델보다 AR 모델이 나은 결과를 냈다는 점이다. 저자들은 DiT와 여러 측면 비교를 정리했는데 :

1. 품질: 2억~20억 규모 VAR가 동일급 혹은 더 큰 DiT-L/2, L-DiT-3B/7B보다 FID/IS가 계속 우수했다 . Precision/Recall도 비슷하거나 더 높았다.
2. 속도: DiT-XL/2는 VAR 대비 45배 느렸고, 30억/70억 파라미터 DiT는 더 느리다 .
3. 데이터 효율: VAR는 350 epoch로 학습되었는데, DiT-XL/2는 1400 epoch를 돌려야 했다 .
4. 스케일링: DiT는 6억→7억→30억 파라미터로 키워도 FID 개선이 미미하거나 오히려 악화되었지만, VAR는 크기 증가에 FID/IS가 꾸준히 향상되어 (표 1, 그림 3) 확실한 scaling law 거동을 보였다 .

결론적으로 VAR는 이미지 생성 품질, 속도, 확장성 측면에서 Diffusion 계열보다 효율적임을 입증하였다 .

5.2 Power-law Scaling Laws

배경

언어 모델 분야에서 모델 파라미터 수 $N$, 훈련 데이터량 $T$, 연산량 $C$와 테스트 loss $L$ 사이에 거듭제곱 법칙 관계가 성립함이 밝혀져 있다 .

예컨대 $L \propto (N^\alpha, T^\beta, C_\text{min}^\gamma)$ 형태로, $\alpha,\beta,\gamma$는 음의 지수를 갖는다 .

이는 모델을 키워도 loss 감소가 점차 둔화되지만 멈추지 않고 계속 줄어듦을 의미하며, 대규모 모델의 성능 예측과 자원 투자 판단에 중요한 지표가 된다 .

VAR의 스케일링 실험

저자들은 VAR Transformer의 depth $d$를 6, 8, 10, … 30까지 변화시키며 (총 12종, 1.85억 ~ 20억 파라미터), 모델 크기별 성능 곡선을 측정했다.

각 모델을 충분히 학습시킨 후 ImageNet 검증셋의 테스트 loss $L$과 token 오류율(정답 token과 다르게 생성된 비율) $Err$을 구했다.

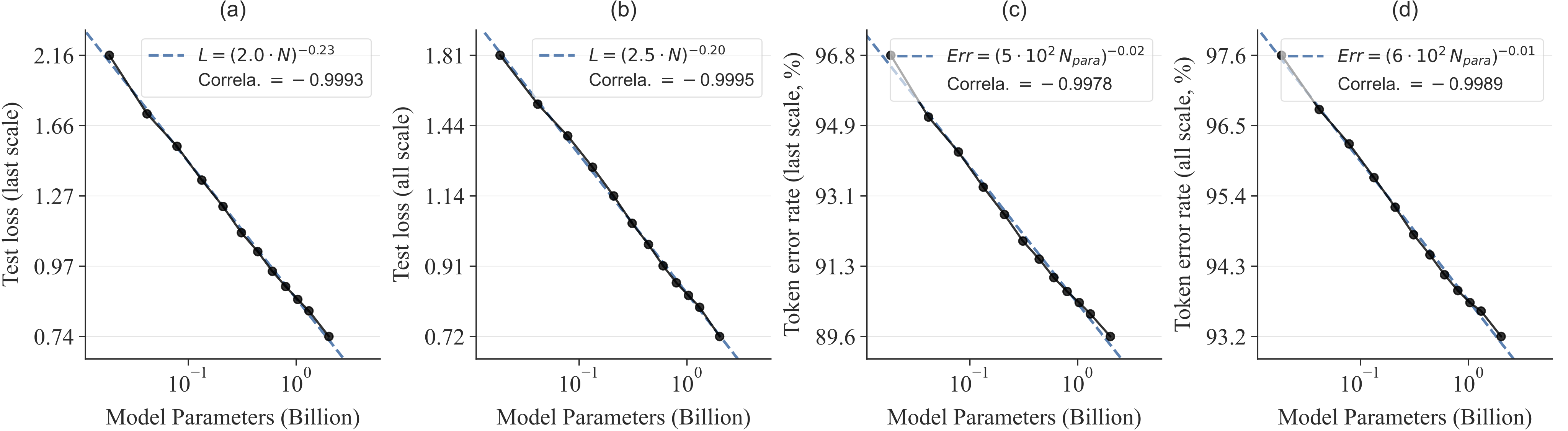
그림 5는 로그-로그 축으로 $N$ 대비 $L$, $N$ 대비 $Err$ 관계를 나타낸 것이다. 그 결과 모델이 커질수록 $L$과 $Err$이 매끄럽게 줄어들며, log-log 상에서 직선에 가까운 경향을 보였다 .

이러한 거의 1에 가까운 피어슨 상관계수는 VAR 모델이 언어 모델과 유사한 스케일링 법칙을 따르고 있음을 의미한다 .

특히 지수 $\alpha$가 0에 근접할수록 스케일 증가에 따른 loss 감소 기울기가 완만하지만 꾸준함을 뜻하는데, VAR에서 실제 관찰된 지수들이 매우 작게 (절댓값 0.01~0.23) 나와 모델을 키울 여지가 충분함을 시사한다 .

이는 “모델을 키울수록 계속 좋아진다”는 LLM의 특성이 시각 AR에서도 확인된 것으로, VAR처럼 효율적인 파라다임 하에서 비로소 드러난 현상이라 할 수 있다 .

Zero-shot Task Generalization

VAR의 zero-shot 일반화 능력을 검증하기 위해, 학습에 사용하지 않은 이미지 편집 관련 작업들을 시도해보았다 .

선택된 작업은

• 이미지 인페인팅(일부 영역 가림 -> 채우기)
• 아웃페인팅(이미지 외연 확장)
• 클래스 조건부 편집(주어진 이미지에서 특정 클래스의 물체를 다른 클래스로 변화)

이다

이러한 작업들은 부분적으로 주어진 이미지 정보를 활용하여 나머지를 생성해야 하므로, 기존 단방향 AR 모델로는 불가능하거나 어려웠다.

저자들은 추가 학습 없이 VAR 모델 (depth 30)을 그대로 활용하였다.

• 인페인팅의 경우, 입력 이미지에서 채워질 부분을 mask하고 나머지 부분은 token으로 변환한 뒤 teacher-forcing으로 Transformer에 제공
  • 그러면 VAR는 주어진 prefix token map들을 조건으로 남은 위치의 token들을 생성한다.
• 아웃페인팅은 입력 이미지를 중앙에 두고, 주변에 빈 패치를 추가로 붙여 동일한 방식으로 진행
• 클래스 조건부 편집은 입력 이미지의 전체 token을 일단 얻은 후, 그 중 편집할 특정 객체 영역을 masking 및 다른 클래스 token으로 채움으로써, 해당 부분만 새 클래스로 변환
  • 이 때 클래스 embedding [s]를 편집 대상 클래스로 설정하여 생성 방향을 유도

위는 이러한 zero-shot 작업의 예시 결과를 보여준다.

VAR는 별도 fine-tuning 없이도 꽤 그럴듯하게 빈 부분을 채우고, 이미지 외연을 확장하며, 객체의 종류를 바꿔치기하는 모습을 보였다 .

이러한 downstream 응용에서의 성능은 VAR 모델이 학습하지 않은 새로운 task에도 적응할 수 있음을 시사한다.

특히 저해상도 token map이 전체 맥락을 제공하고, 고해상도 단계가 세부 묘사를 맡는 VAR의 체계 덕분에, 부분적 단서만으로도 일관성 있는 결과를 낼 수 있었던 것으로 풀이된다.

저자들은 이를 두고 “LLM의 zero-shot 능력을 시각 모델이 모방한 초기 증거”라고 강조한다 .

Ablation Study

VAR의 핵심 기법과 부가 요소들의 효과를 분석하기 위해 ablation study를 수행하였다.

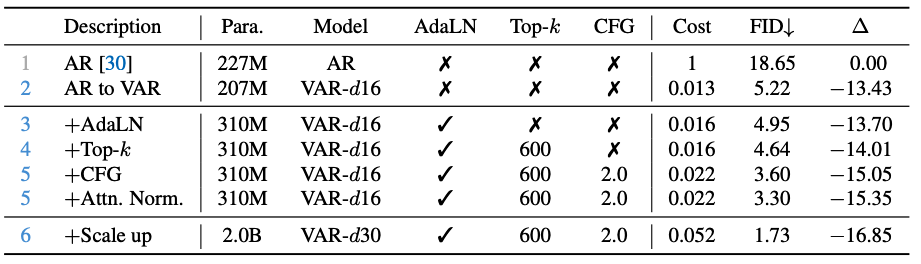
아래 표는 여러 설정 변화에 따른 ImageNet 256×256 FID와 속도 변화를 비교한다 .

• 기본 AR vs. VAR:

  • 1행은 기존 AR Transformer (227M, VQGAN[30] 설정) 결과

  • 2행은 동일 모델을 VAR 방식으로 학습한 결과

    • VAR로 바꾸었을 때 FID가 18.65 → 5.22로 대폭 개선

    • 추론 속도는 1.0 → 0.013로 급격히 향상

      (기존 대비 약 77배 빨라짐)

• Adaptive LayerNorm:

  • 3행은 layer정규화를 AdaLN으로 바꾼 경우

  • 파라미터는 310M로 약간 늘었지만 FID가 5.22 → 4.95로 개선

    이는 AdaLN이 이미지 생성 품질 향상에 기여함을 뜻한다 (기존에도 MaskGIT 등에서 활용된 바 있다).

• Top-k 샘플링:

  • 4행은 생성 시 Top-k=600 제한을 적용한 경우 (무작위 샘플에서 상위 600개 logit만 고려)
  • 이것으로 FID가 4.95 → 4.64로 더 개선
  • 즉 핵 샘플링 기법이 약간의 품질 향상을 주었다.

• Classifier-Free Guidance (CFG):

  • 5행은 CFG를 조건비율 2.0으로 적용한 경우
    • 이는 조건 없는 확률과 조건부 확률을 조합해 샘플링하는 기법으로, diffusion model에서 흔히 쓰인다.
  • 적용 결과 FID가 4.64 → 3.60으로 크게 향상
  • 다만 추론 속도가 약간 느려졌다(1.6%→2.2% baseline 대비).

• Attention Q,K 정규화:

  • 5행에서 추가로 각 Transformer 블록의 쿼리와 키 벡터를 단위 벡터로 정규화하도록 수정

    이는 학습 안정화 아이디어로 제안

  • 적용 후 FID가 3.60 → 3.30으로 더 개선

  • 이때도 여전히 baseline 대비 45× 빠른 속도를 유지

• 모델 스케일 업:

  • 마지막 6행은 모델을 20억 파라미터로 확장 (depth 30)한 경우

  • FID = 1.73을 달성

  • 이는 baseline 대비 16.9p 향상된 것으로, 논문 메인 결과와 일치

  이로써 대형 VAR 모델이 최고 성능을 내는 것을 확인하였다.

요약하면, VAR paradigm 자체로 대폭적인 성능/속도 개선을 얻었으며, 여기에 AdaLN, CFG 등 기법을 추가하고 크기 확장을 하면 추가적인 향상이 이루어졌다.

VAR 알고리즘만으로도 확실한 성능 도약이 있었기에, 부가 요소들은 보조적 역할을 한다고 볼 수 있다.

특히 기존 AR → VAR 전환 (–13.43 FID)의 기여가 가장 크고, 그 다음으로 대형화 (–1.95), CFG (–1.34) 등의 효과가 크다.

결과적으로 VAR-d30 + 모든 트릭이 FID 1.73으로 SOTA 달성했다.

Limitations and Future Work

이번 연구는 학습 패러다임 설계에 초점을 맞춘 관계로, 몇 가지 한계 및 발전 가능성이 남아 있다 :

• tokenizer의 개선 여지:

  • 본 논문에서는 VQGAN(즉 VQ-VAE) 구조를 그대로 사용하여 VAR tokenizer를 구축
    • tokenization 자체는 연구 대상에서 제외하고 VAR 알고리즘의 효과를 검증하려는 의도
  • 따라서 향후 더 진보한 VQVAE tokenizer (예: ViT 기반 또는 더 큰 코드북 등)로 교체하면 표현력 향상에 따라 VAR의 성능도 함께 높아질 가능성이 크다.
  • 이는 본 연구와 직교적인 개선 방향으로서, 최신 연구들의 기법 (예: MaskGIT2, RQ-VAE 개선 등)을 접목해볼 수 있다.

• 텍스트 프롬프트 지원:

  • VAR 자체는 언어 모델과 근본적으로 유사한 구조이므로, 향후 텍스트-투-이미지 생성으로 확장하기 용이

    • 예를 들어 거대 LLM과 결합한 encoder-decoder 구조나, 프롬프트를 바로 컨텍스트로 넣는 in-context learning 방식으로 텍스트 조건부 VAR를 구현할 수 있을 것이다 .

    저자들도 이를 최우선 연구task로 진행 중이라고 밝히고 있다.

• 비디오로의 확장:

  • VAR 개념은 영상 생성에도 자연스럽게 응용 가능

  • 2D 대신 3D (공간+시간) token 피라미드를 구성하고, “3D Next-scale prediction”으로 동영상을 생성하는 것

  • 기존 diffusion 기반 비디오 생성기 (예: SORA) 대비, VAR 접근은 시간 일관성 측면에서 장점이 있을 것으로 기대

  • 또한 기존 AR 비디오 생성은 token 수 폭증으로 비현실적으로 느렸지만, VAR의 효율성으로는 고해상도 영상도 감당 가능하리라 전망

    따라서 VAR를 비디오에 적용하면 장시간 의존성을 다루는 강력한 영상 생성 모델로 발전시킬 수 있을 것

이외에도 VAR의 거대 멀티모달 모델과의 통합, 추론 최적화 등 다양한 후속 연구 방향이 있을 것으로 보인다. 저자들은 VAR가 언어와 시각 간 다리를 놓아 다중모달 지능 발전에 기여하길 기대하고 있다 .

Conclusion

요약하면, 본 논문은 Visual AutoRegressive(VAR)라는 새로운 시각 생성 framwork를 제시하여, 이미지 autoregressive 모델의 기존 한계를 이론적으로 해결하고 성능을 크게 향상시켰다 . VAR는 다음-해상도 예측이라는 개념을 통해 GPT 계열 AR Transformer로 하여금 diffusion model보다 나은 이미지 품질, 다양성, 추론 속도, 데이터 효율을 달성하게 만들었다 . 또 모델 크기 확장에 따른 loss 감소가 power-law를 따르고, downstream zero-shot 활용이 가능함을 보임으로써, 대형 언어모델의 두 가지 핵심 속성(스케일링 법칙, zero-shot 학습)을 시각 모델에서도 구현해냈다 . 이러한 결과는 autoregressive 학습의 범용적 강점이 vision 분야에서도 발휘될 수 있음을 시사하며, NLP 분야의 성공을 시각 분야에 보다 통합하는 데 한 발짝 다가섰다 . 앞으로 공개된 코드와 모델이 활용되어, 시각 autoregressive 및 범용 생성학습 연구가 한층 활성화되고, 강력한 멀티모달 AI 발전으로 이어지기를 기대한다.

한계: 마지막으로, VAR의 현재 한계점을 정리하면 다음과 같다:

• tokenization 부문 발전 필요: 이미지 tokenization는 VQGAN 방식에 머물러 있어 향상 여지가 있음 (더 좋은 tokenizer로 성능 상승 가능) .
• 텍스트 조건 학습 미지원: 현재 클래스 조건만 사용했으며, 자연어 프롬프트를 직접 다루지 못함 (추후 LLM 결합으로 보완 예정) .
• 비디오 생성 미지원: 동영상 생성에 즉시 적용되지는 않았음. 다만 개념적으로 확장 가능하고, 추후 연구로 계획 중임 .

총괄적으로, VAR는 시각 분야 GPT 스타일 모델의 가능성을 열어준 의미있는 성과로서, 후속 연구를 통해 남은 한계들이 보완된다면 향후 확장성 높고 범용적인 이미지/비디오 생성 모델로 발전할 것으로 전망된다.