[Paper Review] WassersteinGAN
[논문 리뷰] WassersteinGAN-wGAN
수학적인, 특히 확률론에 관련된 내용과 글이 많아서 가독성이 떨어질 수 있다.
필자가 예전에 wGAN에서 필요한 수학적 개념들을 정리한 글이 있으니 참고
Introduction
probability distribution, 즉 확률 분포를 학습한다는 것은 확률 밀도(density)를 학습한다는 말이다. 이는 $(P_\theta)_{\theta \in \mathbb{R}_d}$ 의 parametric family를 정의하고, 데이터에서 likehood를 maximize한 밀도를 찾는 방식으로 이루어진다.
parametric family란, 일련의 확률 밀도 함수 또는 확률 분포를 의미한다. 이러한 분포는 parameter set에 의해 결정되며, 이러한 파라미터를 변경함으로써 다양한 분포가 생성될 수 있다.
예를 들어, 정규분포는 평균과 표준편차라는 2개의 파라미터를 가지는 분포이다. 이를 변경함으로써 다양한 형태의 정규분포를 만들 수 있으며, 가능한 모든 정규분포의 집합을 ‘정규분포의 parametric family’라 할 수 있다.
데이터 예시인 $\lbrace x_{i} \rbrace ^m_{i=1}$가 있을 때, 다음과 같은 문제를 해결할 수 있다.
\[\underset{\theta \in \mathbb{R}^d}{\text{max}} \frac{1}{m} \sum_{i=1}^m\log P_\theta(x^{(i)})\]데이터 분포 $\mathbb{P}_r$이 밀도를 가지고, $\mathbb{P}_\theta$가 parametrize된 밀도 $P_\theta$의 분포인 경우, 이는 KL divergence $KL(\mathbb{P}_r || \mathbb{P}_\theta)$를 minimize하는 것과 같다.
위를 설명하려면, 모델의 density(밀도) $P_\theta$가 있어야하지만, 저차원 maniford에서 support하는 분포를 다루는 상황에서는 density가 존재하지 않을 수도 있다.
Maniford란
maniford란 고차원 공간에서 데이터를 설명하는 데 사용되는 저차원 구조이며, 고차원 데이터에서 복잡성을 줄이고, 데이터의 핵심 특징을 추출하는 데 사용된다. 예를 들어, 지구 표면의 작은 부분은 2차원 평면처럼 보이기 때문에 지구 표면은 3차원 공간의 2차원 maniford라고 할 수 있다. 이처럼, maniford는 종종 데이터의 '구조' 또는 '패턴'을 찾는 데 사용되며, maniford 학습은 고차원 데이터에서 maniford를 찾아내는 과정이다.
support
확률론에서 support란, 어떠한 확률 분포나 확률 밀도에서 양수인 값을 가지는 집합을 의미하며, 확률 변수의 가능한 결과들의 집합을 의미한다.
이 경우, 모델 maniford와 실제 데이터 분포의 support가 교집합을 거의 가지지 않으며, 이는 KL distance가 정의되지 않거나 infinite하다는 것을 의미한다.
이 문제를 해결하기 위해 일반적으로 모델 분포에 noise를 추가한다. (실제로 대부분의 Generate 모델에는 Gaussian noise가 포함되어있음.) 하지만, 이러한 잡음이 sample의 품질을 저하시킨다.
확률 밀도 $\mathbb{P}_r$을 직접 추정하는 대신, fixed 분포 $p(z)$를 가지는 random variable $Z$를 정의하고, 이를 매개변수 함수 $g_\theta : \mathcal{Z} \rightarrow \mathcal{X}$를 통해 변환하여 특정 분포 $\mathbb{P}_\theta$를 따르는 sample을 직접 생성할 수 있다.
이 방법은 VAE와 GAN이 사용하며, GAN은 $x$를 결정하는 latent variable $z$를 input으로 하고, $G$와 $D$의 관계를 학습하며 $G$의 분포를 $P(x)$에 가까워지도록 유도한다. 하지만, Mode collapsing이 빈번하게 일어난다는 문제가 있다.
이 논문에서는 모델 분포와 실제 분포간의 거리를 측정하는 다양한 방법, 즉 두 분포 사이의 거리 또는 발산($\rho (\mathbb{P}_\theta \mathbb{P}_r)$)을 정의하는 다양한 방법에 집중한다.
매개변수 $\theta$를 최적화하기 위해서는 모델 분포 $\mathbb{P}_\theta$를 $\theta \rightarrow \mathbb{P}_\theta$라는 mapping이 continuous하도록 해야한다.
continuous한다는 것, 즉 Continuity이란 parameter $\theta_t$가 $\theta$로 converge(수렴)할 때 분포 $P_{\theta_t}$ 역시 $P_\theta$로 수렴한다는 것을 의미
분포 $P_{\theta_t}$의 converge은 거리를 계산하는 방식에 따라 달라진다. 거리가 약할 수록 분포는 converge하기 쉽고 $\theta$space에서 $\mathbb{P}_\theta$space의 continuous mapping을 정의하기 쉬워진다.
왜 연속적이어야 하는가에 대해서는 optimizing algorithm을 생각하면 된다. gradient를 활용하는 경사 하강법은 함수가 연속적이지 않으면 gradient는 증발하거나 무한대가 되기 때문이다.
Different Distances
여기서는 Introduction에서 언급한 다양한 distance에 대해 소개한다.
논문에서 사용하는 표기는 다음과 같다.
- $\mathcal{X}$ : compact metric set (ex- 이미지 공간 $[0,1]^d$)
$\Sigma$ : $\mathcal{X}$의 모든 Borel subset
- $\text{Prob}(\mathcal{X})$ : $\mathcal{X}$에 정의된 확률 측정값의 공간
참 어렵다,,
이제 두 분포 $\mathbb{P}_r, \mathbb{P}_g \in \text{Prob}(\mathcal{X})$사이의 다양한 distance와 divergence를 정의할 수 있다.
Total Variation (TV) distance
\[\delta(\mathbb{P}_r, \mathbb{P}_g) = \underset{A \in \Sigma}{\text{sup}} \left |\mathbb{P}_r(A) - \mathbb{P}_g(A) \right|\]두 확률 분포의 측정값의 차의 상한, 즉 벌어질 수 있는 가장 큰 값을 뜻한다.
Kullback-Leibler (KL) divergence
\[KL(\mathbb{P}_r \parallel \mathbb{P}_g) = \int \log \left(\frac{P_r(x)}{P_g(x)}P_r(x)d\mu(x) \right)\]여기서 $\mathbb{P}_r$와 $\mathbb{P}_g$는 $\mathcal{X}$에 정의된 측정값 $\mu$에 대해 연속적이며, 즉 밀도를 가진다고 가정할 수 있다.
KL divergence는 $\mathbb{P}_g(x) = 0$이고 $\mathbb{P}_r > 0$일때 무한할 수 있으며 비대칭적이다. ($KL(\mathbb{P}_r \parallel \mathbb{P}_g) \neq KL(\mathbb{P}_g \parallel \mathbb{P}_r)$)
Jensen-Shannon (JS) divergence
\[JS(\mathbb{P}_r, \mathbb{P}_g) = KL(\mathbb{P}_r \parallel \mathbb{P}_m) + KL(\mathbb{P}_g \parallel \mathbb{P}_m)\]여기서 $\mathbb{P}_m = \frac{\mathbb{P}_r + \mathbb{P}_g}{2}$이다.
JS divergence는 두 분포에 대한 평균에 대한 KL divergence로 정의되기 때문에 대칭성을 가진다.
Earth-Mover (EM) distance or Wasserstein distance
\[W(\mathbb{P}_r, \mathbb{P}_g) = \underset{\gamma \in \prod(\mathbb{P}_r, \mathbb{P}_g)}{\text{inf}} \mathbb{E}_{(x,y)\sim\gamma}\left[\parallel x-y \parallel \right] \tag{1}\]$\prod(\mathbb{P}_r, \mathbb{P}_g)$는 최댓값이 각각 $\mathbb{P}_r$과 $\mathbb{P}_g$인 모든 joint distribution $\gamma(x,y)$의 집합을 나타낸다.
직관적으로 $\gamma(x,y)$는 분포 $\mathbb{P}_r$을 분포 $\mathbb{P}_g$로 변환하기 위해 $x$에서 $y$로 얼마나 많은 “질량”을 운반해야 하는지를 나타낸다. 그러면 EM distance는 최적의 운반 계획의 “비용”이라고 할 수 있다.
이에 관한 설명은 해당 링크에 매우 잘 설명되어 있다. (wGAN을 이해하는데 큰 도움이 될것이다.)
논문에서는 한가지 예시를 통해 EM distance의 타당성을 제시하고 있다. 아래 참고
Example 1
임의의 확률분포 $\mathbb{P}_0$와 $\mathbb{P}_\theta$를 정의하고 그 사이의 distance와 divergence를 구한다.
$Z \sim U[0,1]$은 $Z$가 0과 1사이의 균일한 분포를 따른다는 것이다. $\mathbb{P}_0$를 $(0, Z) \in \mathbb{R}^2$라고 하자. 이는 $x$는 항상 0이고, $y$축 위 임의의 점 $Z$를 의미한다. $g_\theta (z) = (\theta, z)$는 입력 $z$이며 실수 파라미터인 $\theta$에 의해 결정되는 $(\theta, z)$를 출력한다.
이때, 각 distance는 다음과 같다.
- EM distance : $W(\mathbb{P}_0, \mathbb{P}_\theta) = |\theta|$
- JS divergence : $JS(\mathbb{P}_0, \mathbb{P}_\theta) = \begin{cases} \log 2 & \text{ if }\; \theta \neq 0 \\ 0 & \text{ if } \; \theta = 0 \end{cases}$
- KL divergence : $KL(\mathbb{P}_0 \parallel \mathbb{P}_\theta) = \begin{cases} +\infty & \text{ if }\; \theta \neq 0 \\ 0 & \text{ if } \; \theta = 0 \end{cases}$
- TV distance : $\delta (\mathbb{P}_0, \mathbb{P}_\theta) = \begin{cases} 1 & \text{ if }\; \theta \neq 0 \\ 0 & \text{ if } \; \theta = 0 \end{cases}$
아래 사진은 위에 대해 각각 EM distance(좌)와 JS divergence(우)의 경우를 보여준다.
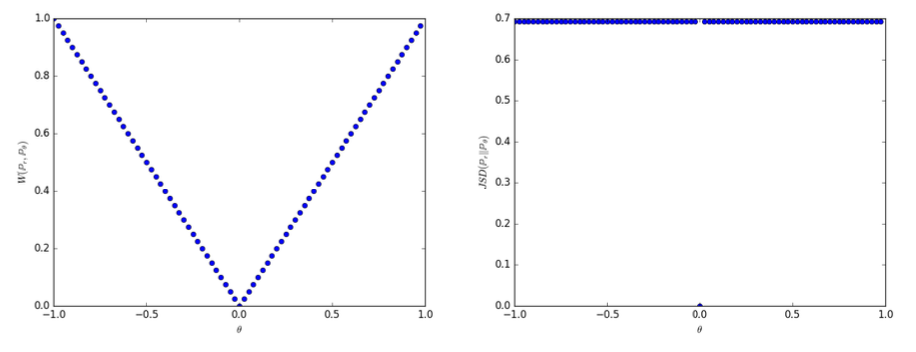
위 Example 1을 통해 EM distance가 JS divergence보다 week하다는 것을 알 수 있다. 그러므로 간단한 가정 하에서 $W(P_r,P_\theta)$가 $\theta$에 대해 연속인 loss function인지 의문을 제기할수 있으며, 아래 Theorem 1을 통해 말하듯이 연속이다.
Theorem 1
$P_r$을 $\mathcal{X}$에 대한 고정 분포이며, $Z$을 다른 space $\mathcal{Z}$에 대한 radom 변수라고 가정하자.$g : \mathcal{Z} \times \mathbb{R}^d$라는 함수라 할때, $g_\theta(z) = (z, \theta)$라 하자. $\mathbb{P}_\theta$는 $g_\theta(Z) $의 분포이다.
- $g$가 $\theta$에 대해 연속이라면, $W(\mathbb{P}_r, \mathbb{P}_\theta$)도 연속이다.
- $g$가 local Lipschitz 조건과 regularity assumption 1을 만족한다면, $W(\mathbb{P}_r, \mathbb{P}_\theta)$는 항상 연속이며 미분가능하다.
- 위의 명제 1, 2는 $JS(\mathbb{P}_r, \mathbb{P}_\theta)$과 모든 KL divergence에 대해서는 성립하지 않는다.
local Lipschitz란 함수의 변화율이 특정한 범위 내에서 제한되어 있음을 말한다. $K$-Lipschitz는 Lipschitz 상수 $K$를 가지며, 다음과 같은 제한이 있다. $$ |f(x_1) - f(x_2)| \leq K|x_1-x_2| $$ 즉, f(x₁)와 f(x₂)를 연결하면 그 gradient는 항상 $K$보다 작은 절대값을 가지며, 이를 함수의 Lipschitz 상수라고 한다. 사인 함수의 경우 도함수의 절대값은 항상 1로 제한되므로 Lipschitz 상수는 1이다. 직관적으로 Lipschitz 연속성은 gradient를 제한하며 딥러닝에서 gradient explosions을 완화하는데 사용된다.
regularity assumption 1
유한한 차원 vetor space 사이의 locally Lipschitz를 $g:\mathcal{Z} \times \mathbb{R}_d \rightarrow \mathcal{X}$라 한다. 아래와 같은 local Lipschitz 상수 $L(\theta,z)$가 있는 경우 $\mathcal{Z}$에 대한 특정 확률 분포 $p$에 대해 $g$가 가정 1을 만족한다고 한다. $$ \mathbb{E}_{z \sim p} \left [L(\theta, z) \right] < + \infty $$
Neural Network에서 EM distance를 minimize하여 train하는 것이 이론적으로 합리적임을 다음을 통해 말한다.
Corollary 1
$g_\theta$는 $θ$로 parameterize된 feedfoward Neural Network이고, $p(z)$는 $\mathbb{E}\_{z \sim p(z)} [\parallel z \parallel] < \infty$ (Gaussian, uniform 등)이 되도록 하는 $z$에 대한 사전분포라고 가정하자. 그러면 위 assumption 1이 충족되므로 $W(\mathbb{P}_r,\mathbb{P}_θ)$는 모든 곳에서 연속적이고 거의 모든 곳에서 미분 가능하다.이 모든 것은 EM distance가 적어도 JS divergence보다 훨씬 더 합리적인 cost function이라는 것을 보여주며 위상의 상대적 강도는 다음과 같다.
\[\underset{strong \;\;\;\rightarrow \;\;\;week}{\text{KL} > \text{(JS, TV)} > \text{EM}}\]Wasserstein GAN
EM distance인 Eq. 1의 극한은 매우 intractable하다. Eq. 1에서의 $\mathbb{P}_r$과 $\mathbb{P}_g$의 joint distribution을 구해야 하지만, $\mathbb{P}_r$는 우리가 알고자 하는 대상이기 때문이다.
그래서 Kantorovich-Rubinstein duality를 이용해서 다음과 같이 바꿀 수 있다.
\[W(\mathbb{P}_r, \mathbb{P}_\theta) = \underset{\parallel f\parallel _L \leq1}{\text{sup}}\; \mathbb{E}_{x \sim \mathbb{P}_r}[f(x)] - \mathbb{E}_{x \sim \mathbb{P}_\theta}[f(x)] \tag{2}\]$\parallel f\parallel _L \leq1$에서 1 대신 $K$를 대입하면, $K \cdot W(\mathbb{P}_r, \mathbb{P}_\theta)$가 된다. 이는 임의의 상수 $K$에 대해 $K$-Lipschitz를 고려하는 것이다.
supremum, 즉 $\text{sup}$은 주어진 집합에서 가장 큰 상한을 의미한다. 이는 주어진 집합의 모든 원소보다 크거나 같은 가장 작은 숫자를 찾는 것을 의미하며 즉, 어떤 집합의 모든 원소를 넘지 않으면서 그 집합의 상한인 수를 의미한다.
이는 ‘최대값(maximum)’과는 다른 개념이다. 최대값은 집합의 원소 중에서 가장 큰 값을 의미하지만, supremum은 집합의 원소가 아니어도 된다.
예를 들어, 0과 1 사이의 모든 실수를 포함하는 집합의 최대값은 정의되지 않지만, supremum은 1이다.
그러므로, paramerize된 함수의 가족 $\lbrace f_w \rbrace_{w \in \mathcal{W}} $이 $K$-Lipschitz 인 경우 다음과 같은 문제를 해결할 수 있다.
즉, parameterize된 함수 $f_w$로 바꾸고, $\mathbb{P}_\theta$를 $g_\theta$에 관한 식으로 바꾸면 다음과 같은 식을 구할 수 있다.
\[\underset{w\in \mathcal{W}}{\text{max}}\; \mathbb{E}_{x \sim \mathbb{P}_r} [f_w(x)] - \mathbb{E}_{z\sim p(z)}[f_w(g_\theta(z))] \tag{3}\]Eq. 3은 GAN의 loss식과 유사해 보이며, 이 식에서 존재하는 $\mathbb{P}_r$에 대한 의문점이 생길 수 있다. 실제로는 학습된 $D$가 그 역할을 해주며, gradient를 update할 때 $\theta$에 대해 미분하기 때문에 앞 항은 사라진다. (wGAN에서는 $D$를 critic으로 대체한다. 추후 설명)
논문에 있는 Theorem 3은 위 식 Eq. 3을 미분한다.
\[\bigtriangledown _\theta W(\mathbb{P}_r, \mathbb{P}_\theta) = -\mathbb{E}_{z\sim p(z)}[\bigtriangledown _\theta f(g_\theta(z))]\]우리는 Eq. 2의 maximize 문제를 해결하기 위한 함수 $f$를 찾아야한다. 이를 위해 가중치 $w$로 parameterize한 신경망을 사용하며 GAN에서의 Discriminator 역할을 하게 된다. WassersteinGAN에서는 이를 critic이라 명명한다.
Eq. 3은 critic의 loss 식이자, EM distance를 의미하며 $w$는 그 critic($f$)의 파라미터이다.
$f_w$가 compact space $\mathcal{W}$으로 제한하기 위해서 gradient update 후에 $w$를 $[-0.01, 0.01]$ 사이로 조정하며, 이를 Weight clipping이라고 한다.
Weight clipping은 Lipschitz 조건을 적용하기 위해 넣었지만, 그렇게 좋지 못한 방법이라고 논문에서 말한다. 이 논문에서는 단순하고 이미 성능이 좋다고 알려진 정도의 clipping을 적용하였으며, Neural Network에서 Lipschitz 조건을 적용하는 문제는 추후 연구를 위해 남겨 놓았다고 말한다.
WassersteinGAN의 Generator loss fuction은 Theorem 3에 나와있듯이, Eq. 3을 $\theta$에 대해 미분하여 앞의 항을 사라지게 하여 얻을 수 있다.
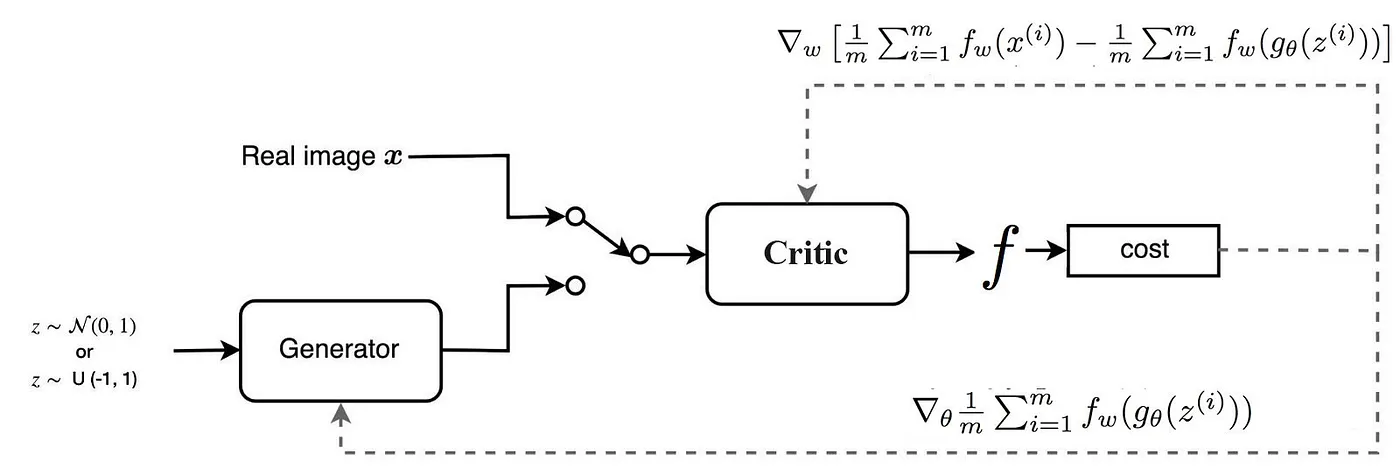
위 그림은 wGAN의 아키텍처를 표현한 그림(출처)이며 Algorithm 1에 설명되어있다.
위 알고리즘을 천천히 뜯어보자.
- $n_{\text{critic}}$ 횟수만큼 critic을 update한다.
- $\mathbb{P}_r$과 $p(z)$를 각각 mini batch 만큼 sampling한다.
- critic loss function을 이용해서 파라미터 $w$를 update한다. (Adam 대신 RMSProp)
- clip($w, -c, c$)부분은 위에서 언급한 Weight clipping을 수행한 것이다.
- critic update가 끝나면 $G$를 loss function에 맞게 update한다.
GAN의 $D$는 이미지가 real인지 fake인지 sigmoid 확률값을 사용해 판단하며 gradient 정보는 사용되지 않는다.
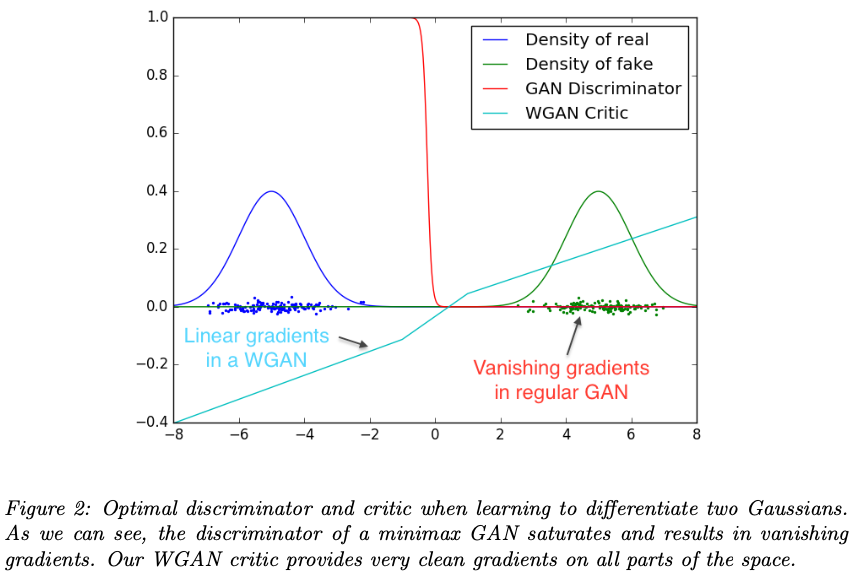
하지만 wGAN의 critic은 EM distance의 식을 그대로 사용하기 때문에, gradient를 제공하는 linear function으로 수렴한다. 즉, output이 scalar값으로 이미지의 진위 여부를 점수처럼 표시한다.
위 사진을 보면 GAN의 $D$는 Gradient vanishing 문제가 생겼으며, WGAN은 안정적인 linear한 형태를 띄고 있음을 알 수 있다.
EM distance가 연속적이고 미분 가능하다는 것은 critic을 optimal 할때까지 계속 train 할 수 있다는 의미이며, 기존 GAN이 가지고 있던 mode collapse문제와 $G$와 $D$간의 balance 붕괴 문제가 해결되는 것이다.
Empirical Results
저자들은 WassersteinGAN 알고리즘을 사용하여 이미지 생성 실험을 진행하였을 때, 2가지 이점을 얘기한다.
- $G$의 수렴과 sample의 품질에 영향을 미치는 loss metric
- Optimization process의 안정화
Experimental Procedure
Train에 사용한 데이터는 LSUN-Bedroom dataset이며 WGAN과 비교 대상은 DCGAN의 아키텍쳐를 따른 GAN이다.
Meaningful loss metric
첫 번째 실험은 이 추정치가 생성된 샘플의 품질과 얼마나 잘 상관관계를 가지는지를 보여준다.
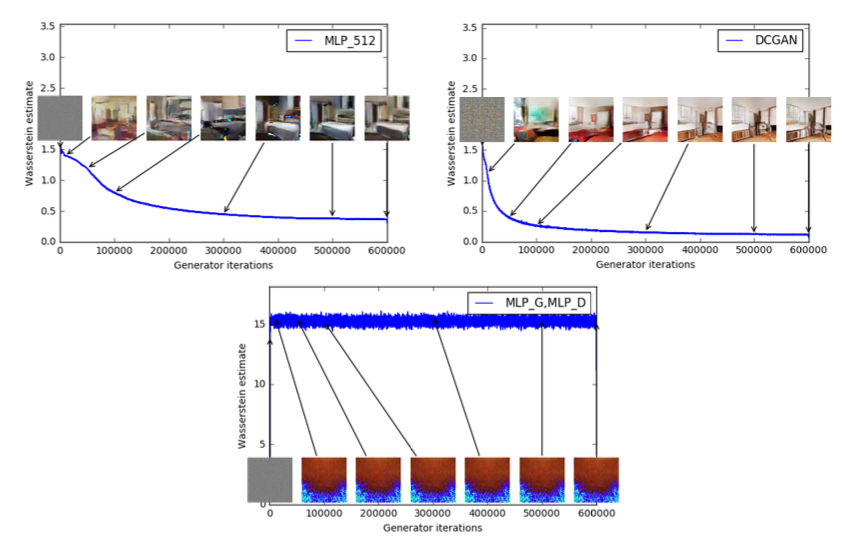
DCGAN 아키텍처 외에도, $G$ 또는 $G$와 critic 모두를 512개의 hidden unit을 가진 4-layer ReLU-MLP(Multi-Layer Perceptron)로 교체하는 실험도 진행하였다.
- 좌측 상단 : $G$만 4-layer ReLU-MLP로 교체한 결과
- 학습이 진행될수록 sample 품질은 향상되고 loss는 감소
- 우측 상단 : 표준 DCGAN
- loss는 빠르게 감소하고 sample 품질도 그에따라 증가
상단 2개의 plot은 모두 critic에 sigmoid가 없는 DCGAN이므로 비교할수 없다.
- 아래쪽 : $G$와 $D$모두 4-layer ReLU-MLP로 교체
- 학습률이 상당히 높은 MLP라서 학습 실패
- loss와 sample이 모두 일정하다.
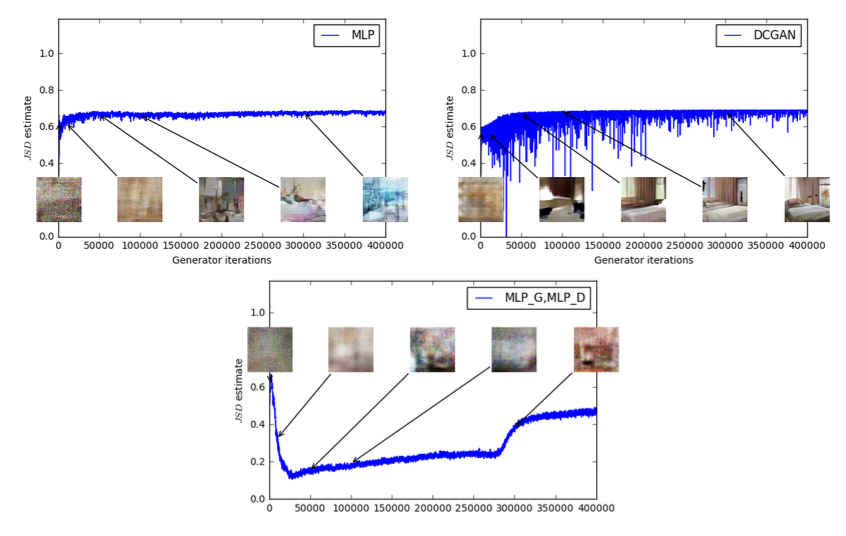
위 plot은 같은 모델로 실험을 진행하되, 각 iter 마다 JS Divergence를 계산한 그래프이다. sample 품질이 좋아져도 JS Divergence는 증가하거나 상수 값을 유지하는 것을 알 수 있다.
실제로 JS Divergence의 max인 $\log 2 ≈ 0.69$에 매우 근접하는 경우가 많다. 즉, JS Divergence가 포화되고 $D$의 loss가 0가 되며 생성된 sample이 어떤 경우에는 meaningful한(오른쪽 상단 플롯) 반면 어떤 경우에는 무의미한 이미지가 되기도 한다.
또한, 기존에는 Optimizer로 Adam을 사용했는데, 이와 같은 momentum기반 optimizer나 높은 train 속도를 사용하는 경우 WGAN의 train이 불안정해진다고 한다. critic의 loss는 fix되어있지 않기 때문에, momentum 기반 대신, non-fixed 문제에도 잘 작동하는 RMSPorp를 사용하였다고 한다.
Improved stability
WassersteinGAN은 최적의 critic으로 train할 수 있다는 장점이 있다. 기존의 GAN은 $D$와 $G$의 balance를 맞추며 학습해야했다. 하지만 wGAN은 critic이 완전히 train되면, $G$에 loss를 제공하기만 하면 되며 $G$의 gradient 품질은 critic의 성능에 비례한다.
DCGAN의 $G$를 사용하되, 여러 변화를 주어서 실험하여 $D$와 critic을 비교하였다. (즉, WGAN과 GAN을 비교함 셈)
논문에서는 실험할 때 WGAN에서는 mode collapse가 발견된적이 없다고 한다.
즉, WGAN은 GAN의 학습 과정을 안정화시키는 데 큰 기여를 했다. EM distance를 사용하여 optimal한 지점에 도달할 수 있게 되었다. 이러한 변형은 mode collapse 를 해결함으로써 다양한 sample을 생성할 수 있게 하여 기존의 GAN이 가지고 있던 문제들을 해결하였다고 한다.